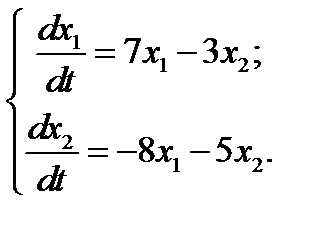Образец выполнения задания № 4. Задача.Уменьшение интенсивности света, прошедшего через слой какой-либо среды
Задача.Уменьшение интенсивности света, прошедшего через слой какой-либо среды, пропорционально толщине слоя и интенсивности падающего на него света. Известно, что при прохождении через слой толщины 1 см интенсивность уменьшается в 2 раза. Во сколько раз уменьшится интенсивность при прохождении через слой толщины 5 см?
Решение. Пусть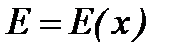 
- интенсивность света, падающего внутри среды на поверхность, координата которой х (рис. 1). Согласно условию, при прохождении через последующий бесконечно тонкий слой dx начальная интенсивность уменьшится на величину 
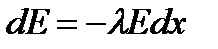, где 
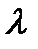- коэффициент пропорциональности. Найдем общее решение этого уравнения
, 
, 
, 
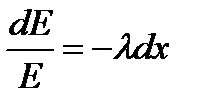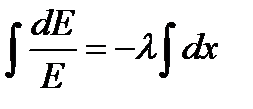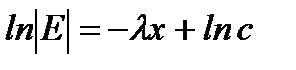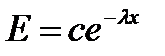. (А)
| Е(х) |
| слой среды |
| х dx |
| х |
Рис. 1
Возьмем произвольный слой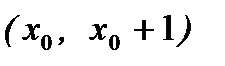 
, толщина которого 1 см. Пусть при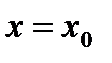 
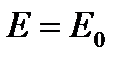, тогда по условию при 
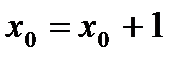будет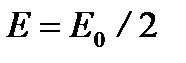 
. Подставив эти значения в (А), получим 
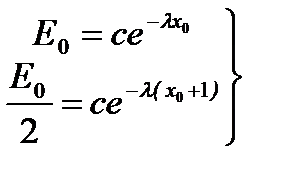, отсюда находим 
, 
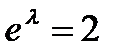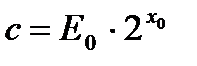. Подставив эти значения в (А), получим 
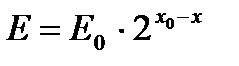. Возьмем 
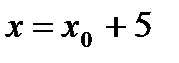- поверхность, удаленная от начальной 
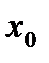на 5 см. Тогда интенсивность будет равна 
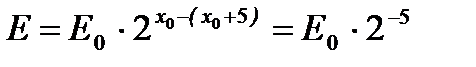. Отношение исходной интенсивности 
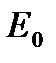к конечной 
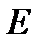равно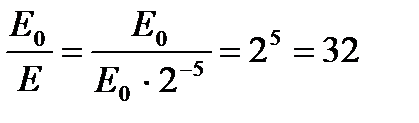 
, т.е. интенсивность уменьшилась в 32 раза.
Образец выполнения задания № 5
Задача.Найти общее решение системы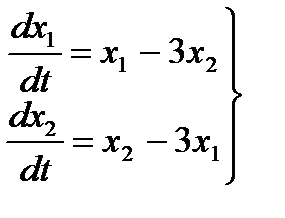 
.
Решение. Из первого уравнения находим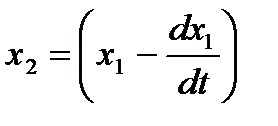 
(А), подставим во второе уравнение 
, 
, 
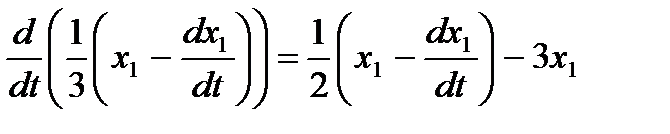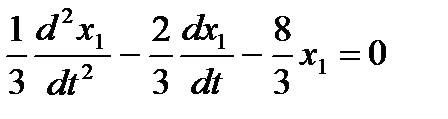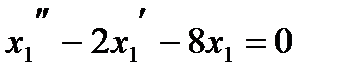- получилось линейное однородное уравнение с постоянными коэффициентами. Его характеристическое уравнение 
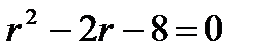имеет корни 
, 
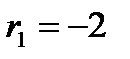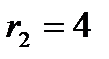, поэтому 
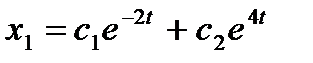. Подставив в (А), получим 
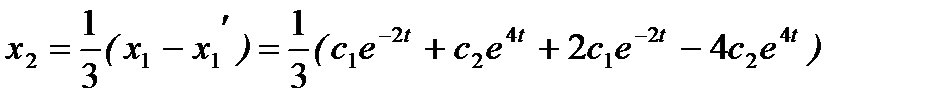. Следовательно, общее решение системы имеет вид , 
.
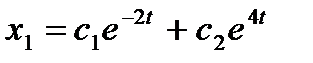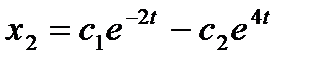ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 7
Задание № 1
Найти общее решение дифференциального уравнения первого порядка.
1. 
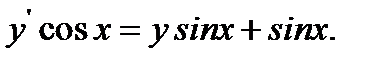
2. 
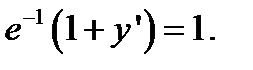
3. 
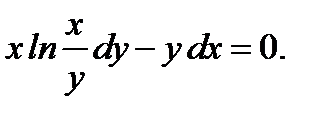
4. 
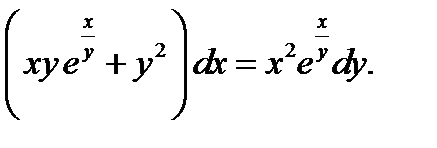
5. 
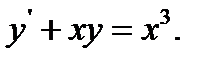
6. 
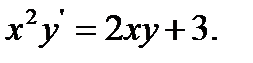
7. 
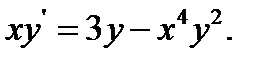
8. 
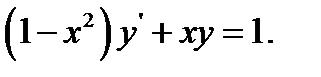
9. 
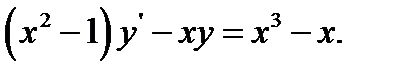
10. 
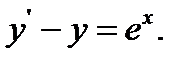
11. 
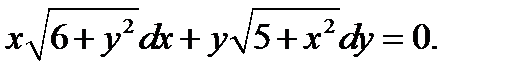
12. 
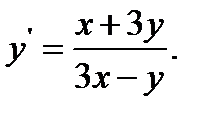
13. 
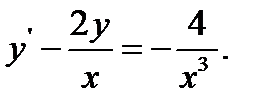
14. 
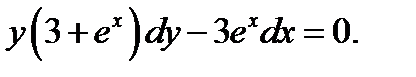
15. 
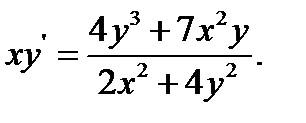
16. 
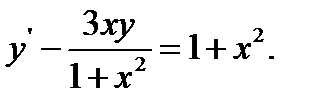
17. 
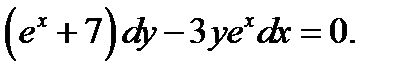
18. 
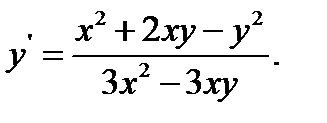
19. 
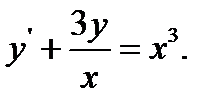
20. 
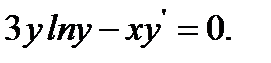
21. 
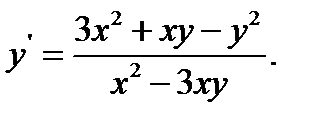
22. 
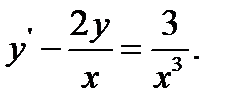
23. 
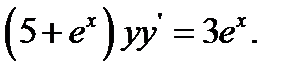
24. 
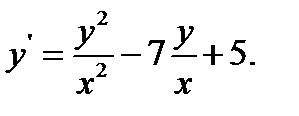
25. 
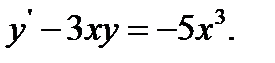
26. 
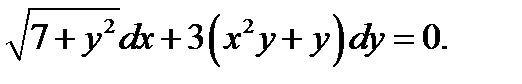
27. 
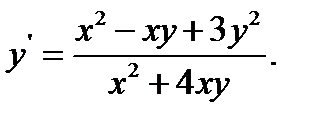
28. 
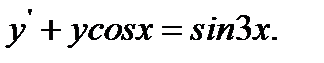
29. 
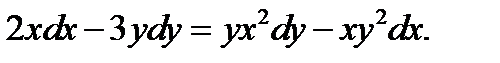
30. 
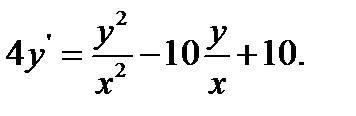
Задание № 2
Найти общее решение дифференциального уравнения второго порядка.
1. 
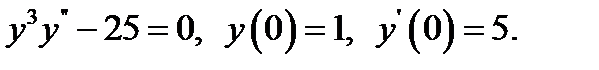
2. 
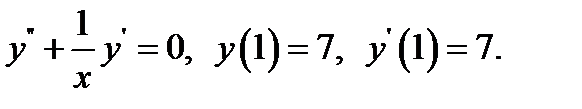
3. 
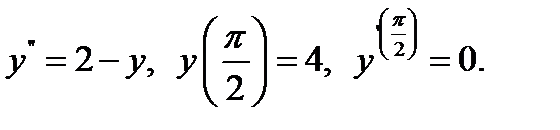
4. 
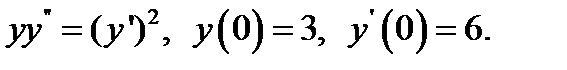
5. 
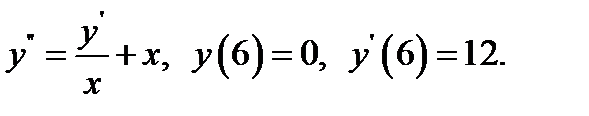
6. 
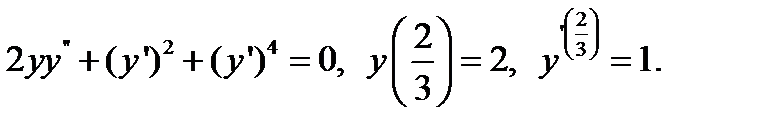
7. 
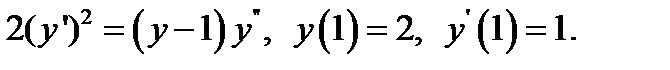
8. 
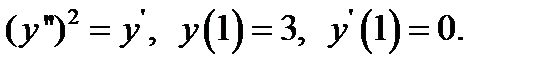
9. 
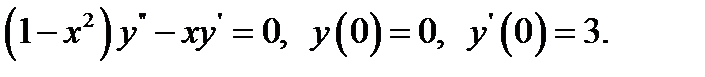
10. 
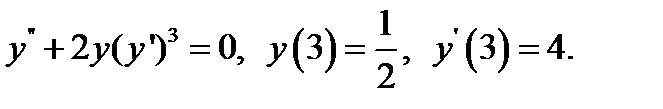
11. 
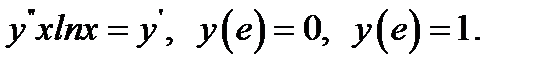
12. 
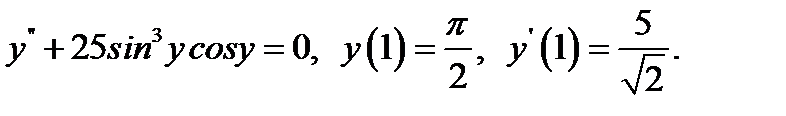
13. 
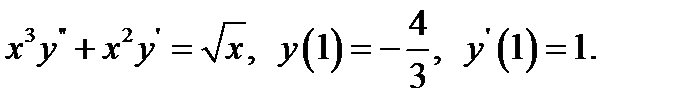
14. 
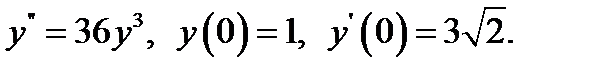
15. 
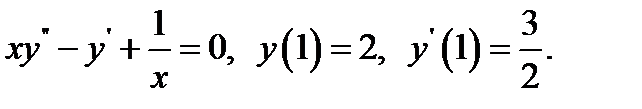
16. 
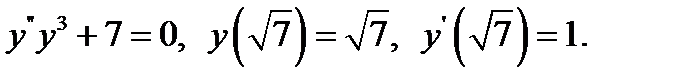
17. 
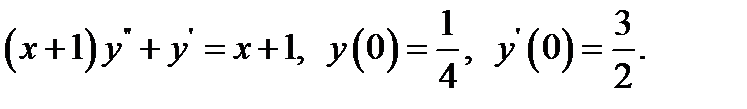
18. 
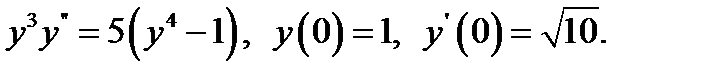
19. 
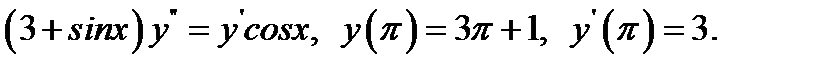
20. 
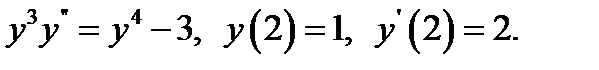
21. 
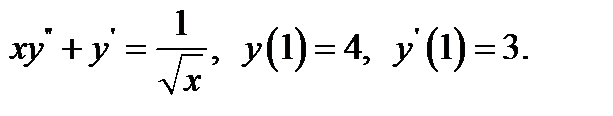
22. 
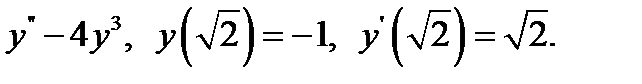
23. 
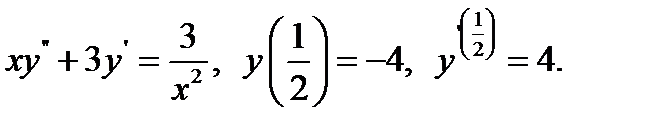
24. 
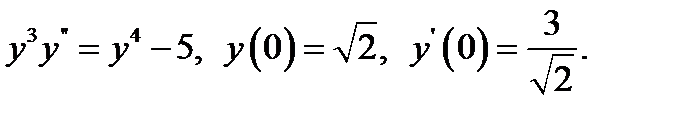
25. 
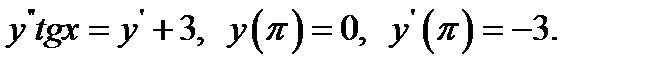
26. 
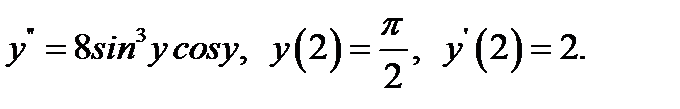
27. 
28. 
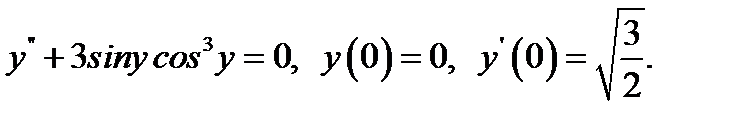
29. 
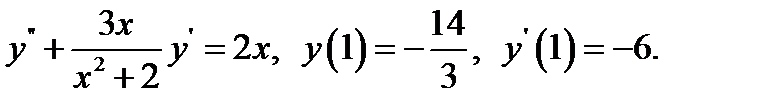
30. 
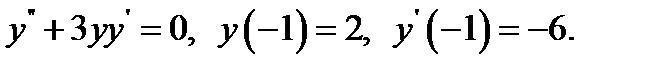
Задача № 3
Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
1. 
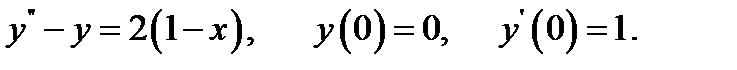
2. 
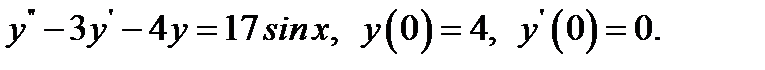
3. 
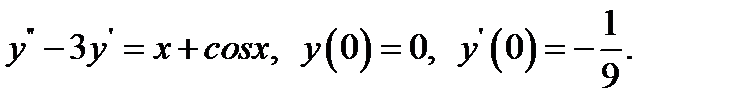
4. 
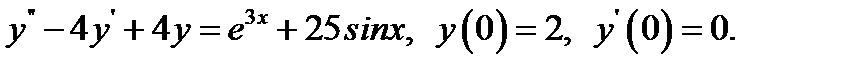
5. 
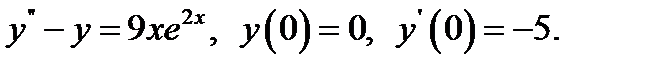
6. 
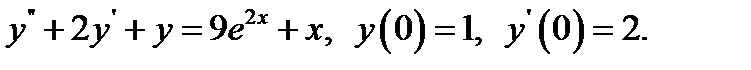
7. 
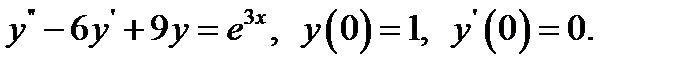
8. 
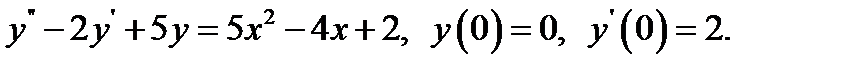
9. 
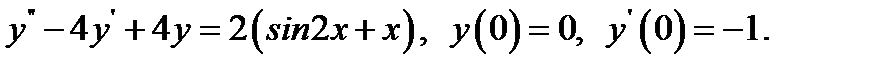
10. 
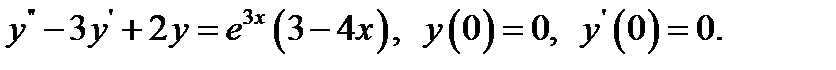
11. 
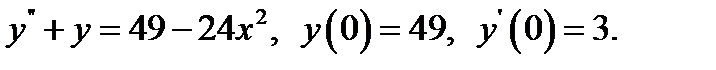
12. 
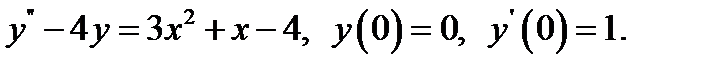
13. 
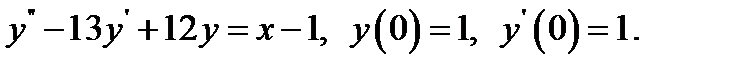
14. 
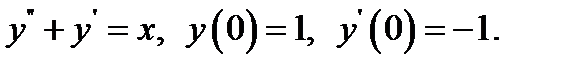
15. 
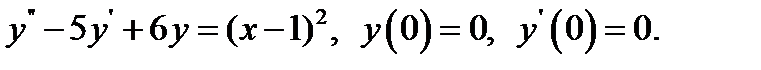
16. 
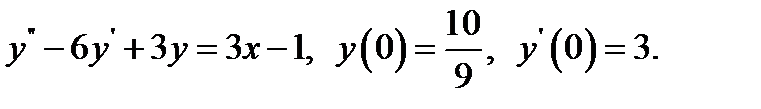
17. 
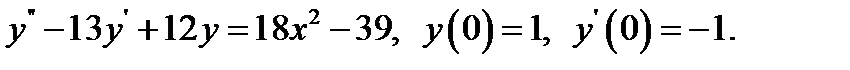
18. 
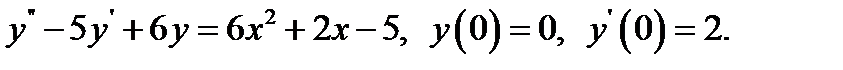
19. 
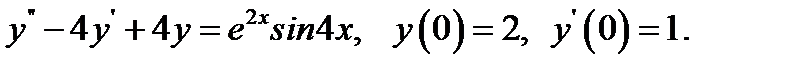
20. 
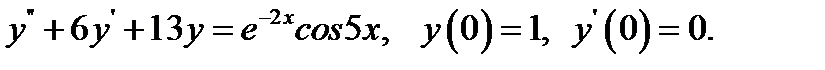
21. 
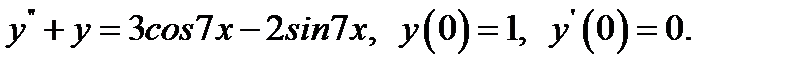
22. 
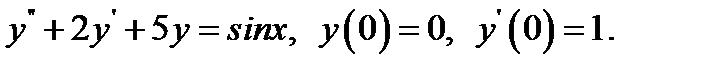
23. 
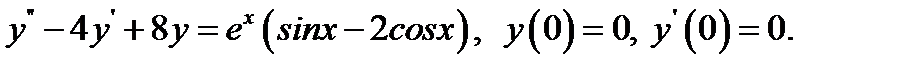
24. 
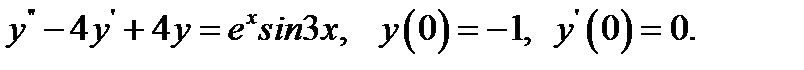
25. 
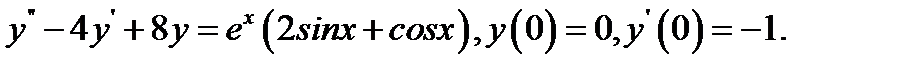
26. 
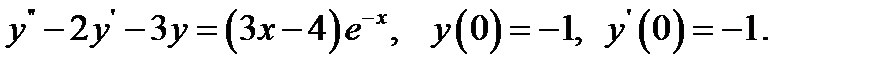
27. 
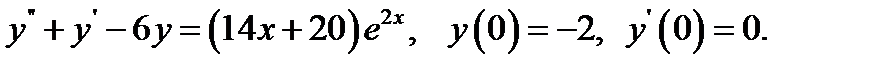
28. 
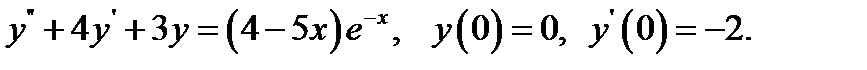
29. 
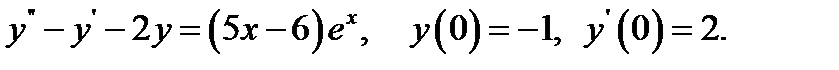
30. 
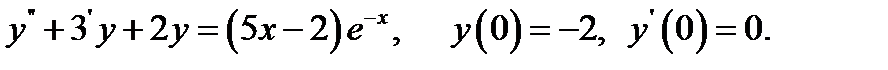
Задача № 4
1. Тяжелое тело без начальной скорости скользит по наклонной плоскости. Найти путь, пройденный телом за время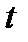 
, если угол наклона равен 
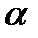, а коэффициент трения равен 
.
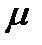2. Найти зависимость давления воздуха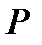 
от высоты 
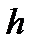, если известно, что это давление равно 1 
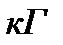на 1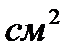 
на уровне моря 
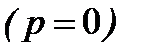и 0,92 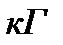на 1 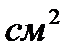на высоте 500 
.
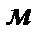3. Материальная точка массы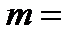 
2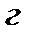 
без начальной скорости медленно погружается в жидкость. Найти путь, пройденный точкой за время 
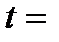1 с, считая, что при медленном погружении сила сопротивления жидкости пропорциональна скорости погружения (коэффициент пропорциональности 
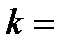2).
4. В резервуаре находится 100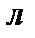 
раствора, содержащего 10 
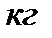растворенной соли. В резервуар втекает вода со скоростью 3 
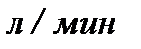, а смесь вытекает со скоростью 2,5 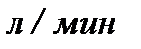, причем концентрация поддерживается равномерной путем перемешивания. Сколько соли останется в резервуаре по истечении часа.
5. Катер движется в спокойной воде со скоростью V = 10 км/ч. На полном ходу его двигатель был выключен, и через 2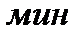 
скорость катера уменьшилась до V = 0,5 км/ч. Определить скорость, с которой двигался катер через 40 с после выключения двигателя, считая сопротивление воды пропорционально скорости движения катера.
6. Найти уравнение кривой, если длина отрезка касательной от точки касания до пересечения ее с осью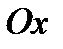 
имеет постоянную длину 
.
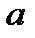7. Найти уравнение кривой, проходящей через точку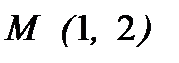 
и обладающей тем свойством, что отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении 2:3, считая от оси ординат.
8. Найти уравнение кривой, радиус кривизны которой равен постоянной величине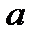 
.
9. Найти уравнение кривой, проходящей через точку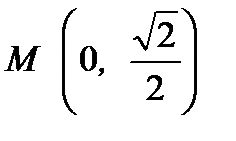 
и обладающей тем свойством, что касательная к ней в точке с координатами 
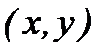проходит через точку с координатами 
.
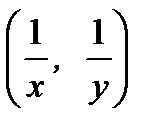10. Найти уравнение кривой, проходящей через точку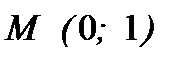 
и обладающей тем свойством, что касательная к ней в любой точке пересекает прямую 
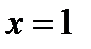в точке, ордината которой в три раза больше ординаты точки касания.
11. Кривая проходит через точку 
. В произвольной точке этой кривой проведена касательная. Точка пересечения касательной с осью Ох имеет абсциссу, вдвое большую, чем абсцисса точки касания. Найти уравнение кривой.
12. В комнате, где температура 20 
С, тело остыло за 20 мин от 100 до 60°С. Найти закон охлаждения тела. Через сколько минут оно охладится до 30°С? Повышением температуры в комнате пренебречь.
13. Составить уравнение линии, проходящей через точку М (0; 3), если угловой коэффициент касательной в любой точке линии равен произведению координат точки касания.
14. Точка массой 4 г движется прямолинейно без начальной скорости. На точку действует сила, пропорциональная времени с коэффициентом пропорциональности 22 м/с3. Кроме того, на точку действует сила сопротивления среды, пропорциональная скорости с коэффициентом пропорциональности 3 г/с. Найти зависимость скорости от времени.
15. Составить уравнение линии, у которой площадь треугольника, построенного на абсциссе любой точки и начальной ординате касательной в этой точке есть величина постоянная, равная 9.
16. Находящееся в жидкости тело массы 6 кг под действием собственного веса погружается вниз без начальной скорости. Сопротивление жидкости прямо пропорционально скорости тела с коэффициентом пропорциональности 3 кг/с. Найти закон движения тела (зависимость пути от времени).
17. Составить уравнение линии, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания.
18. Согласно опытам, в течение года из каждого килограмма радия распадается 0,44 г. Через сколько лет распадается половина имеющегося количества радия? (Количество распадающегося вещества за единицу времени пропорционально имеющемуся количеству вещества).
19. Футбольный мяч массы 0,4 кг брошен вверх со скоростью 20 м/с. Сопротивление воздуха пропорционально квадрату скорости и равно 0,48 Н при скорости 1 м/с. Вычислить время подъема мяча.
20. Найти кривую, у которой точка пересечения касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.
21. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/с, через 4 с скорость её 1 м/с. Какой путь пройдет лодка до её остановки?
22. Найти кривую, у которой расстояние между касательной и началом координат равно абсциссе точки касания.
23. Мяч падает с высоты 16,3 м без начальной скорости. Сопротивление воздуха пропорционально квадрату скорости и равно 0,48 Н при скорости 1 м/с. Найти скорость в конце падения.
24. Найти уравнение кривой, у которой точка пересечения касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
25. Резиновый шнур длиной 1 м под действием силы 5 Н удлиняется на 0,05 м. На сколько удлиняется такой же шнур длины 10 м и веса 40 Н под действием своего веса, если его подвесить за один конец?
26. Составить уравнение линии, у которой площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, равна 48.
27. Цилиндрический бак имеет отверстие в дне и поставлен вертикально. Из полного бака половина воды вытекает за 5 мин. За какое время вытечет вся вода? (Из сосуда жидкость вытекает со скоростью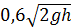 
, где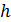 
- высота воды над отверстием).
28. Найти кривую, у которой радиус кривизны обратно пропорционален косинусу угла между касательной и осью абсцисс. (Радиус кривизны определяется по формуле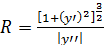 
).
29. Найти атмосферное давление на высоте 1 км, если на поверхности земли давление равно 9,8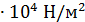 
и плотность воздуха 1,2 кг/ 
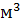. (Использовать закон Бойля-Мариотта: плотность пропорциональна давлению).
30. Найти кривую, проходящую через точку (2; 4), у которой отрезок касательной, заключенный между осями координат, делится в точке касания пополам.
Задача № 5
Найти общее решение системы дифференциальных уравнений.
1. 
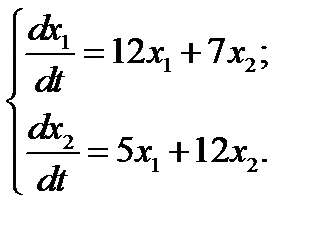
2. 
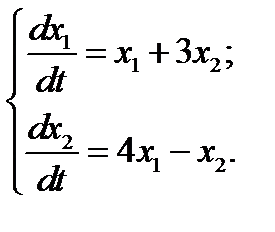
3. 
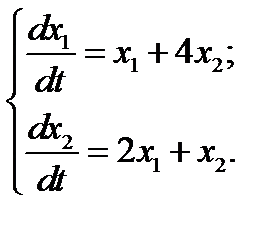
4. 
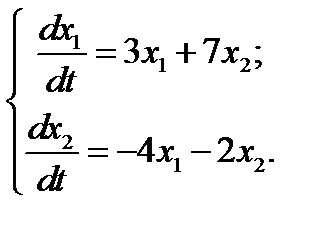
5. 
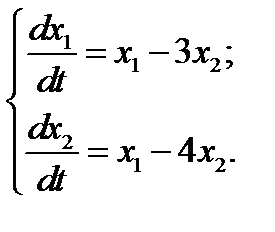
6. 
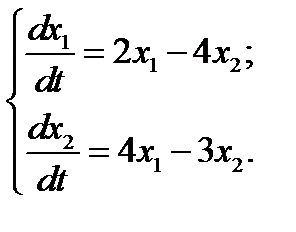
7. 
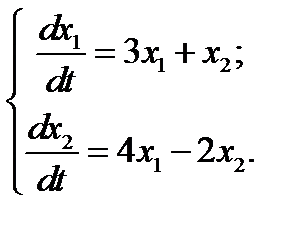
8. 
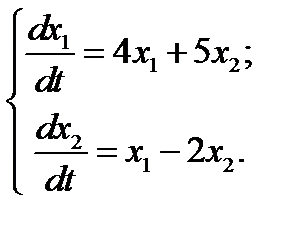
9. 
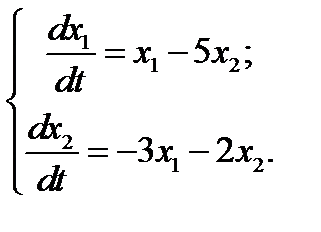
10. 
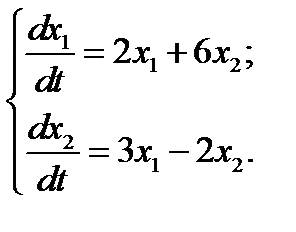
11. 
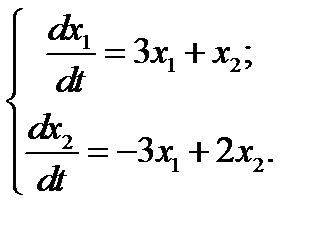
12. 
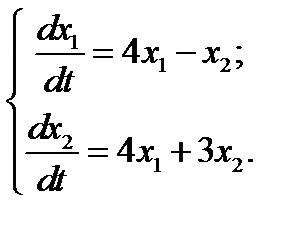
13. 
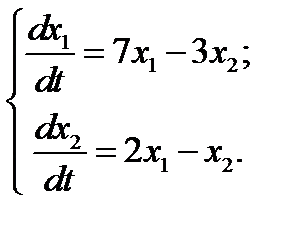
14. 
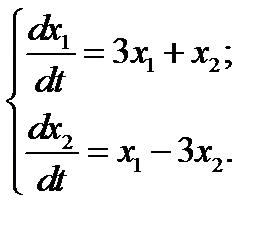
15. 
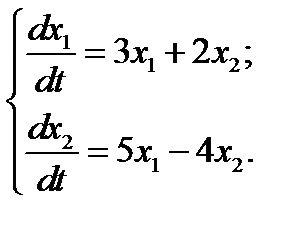
16. 
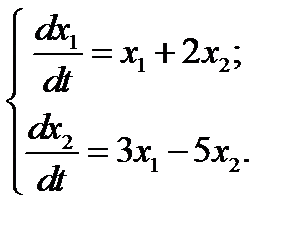
17. 
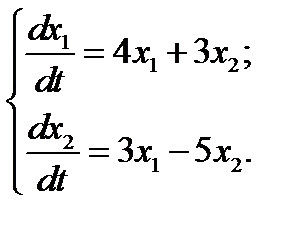
18. 
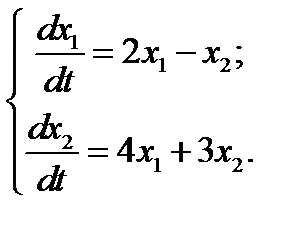
19. 
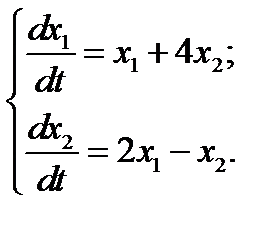
20. 
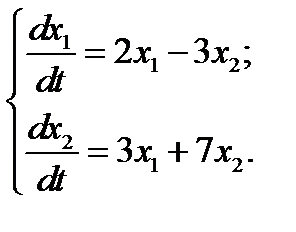
21. 
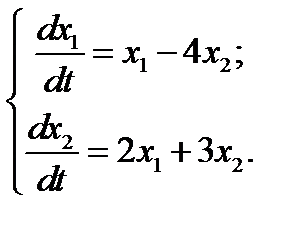
22. 
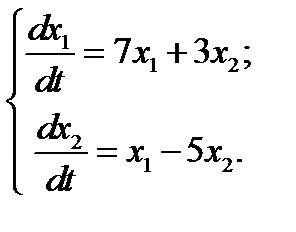
23. 
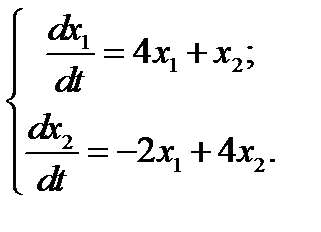
24. 
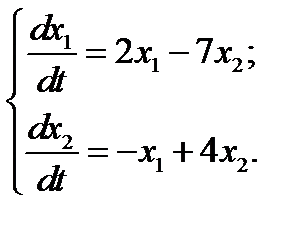
25. 
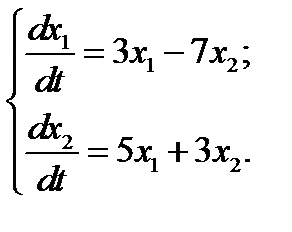
26. 
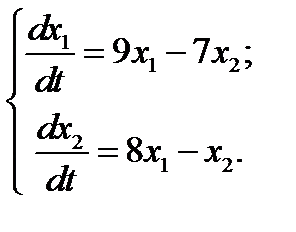
27. 
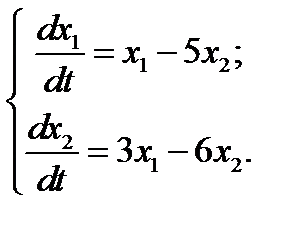
28. 
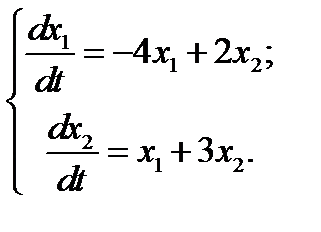
29. 
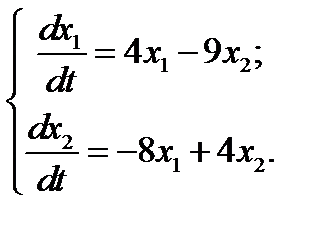
30. 