Образец выполнения задания № 2
Задача. Дана функция 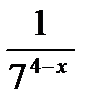 и значения аргумента
и значения аргумента 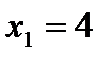 ,
, 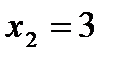 . Найти:
. Найти:
1) Точку 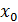 , в которой функция не определена.
, в которой функция не определена.
2) Найти односторонние пределы функции в точке 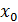 .
.
3) Найти предел функции при 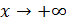 и при
и при 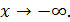
4) Сделать схематический чертеж.
Решение: Исследуем на непрерывность в точке 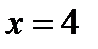 . По определению: функция
. По определению: функция 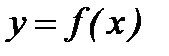 непрерывна в точке
непрерывна в точке 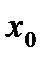 , если
, если 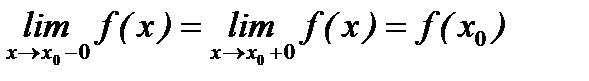 .
.
1) Знаменатель дроби 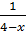 приравняем к нулю, получим
приравняем к нулю, получим 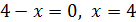 . Значит,
. Значит, 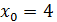 - точка, в которой функция не определена.
- точка, в которой функция не определена.
2) Находим предел слева от точки 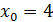 :
:
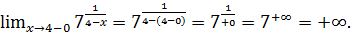 Итак, при
Итак, при 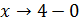 происходит
происходит 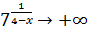 - график уходит вверх (рис. 5).
- график уходит вверх (рис. 5).
Находим предел справа от точки 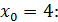
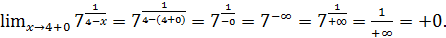 Итак, при
Итак, при 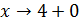 происходит
происходит 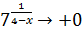 - график приближается сверху к точке
- график приближается сверху к точке 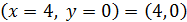 (рис.6).
(рис.6).
3) 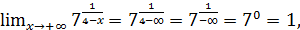
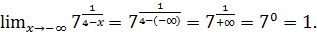
| х |
| у |
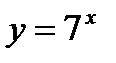 |
Рис. 6
Образец выполнения задания № 3
Задача.Найти производную 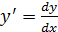 функций.
функций.
1) 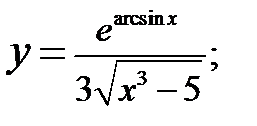 2)
2) 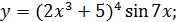 3)
3) 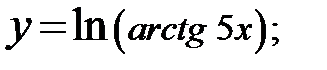
4) 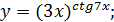 5)
5) 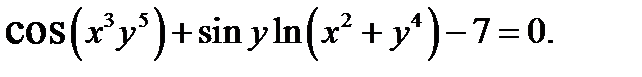
Решение:
1) 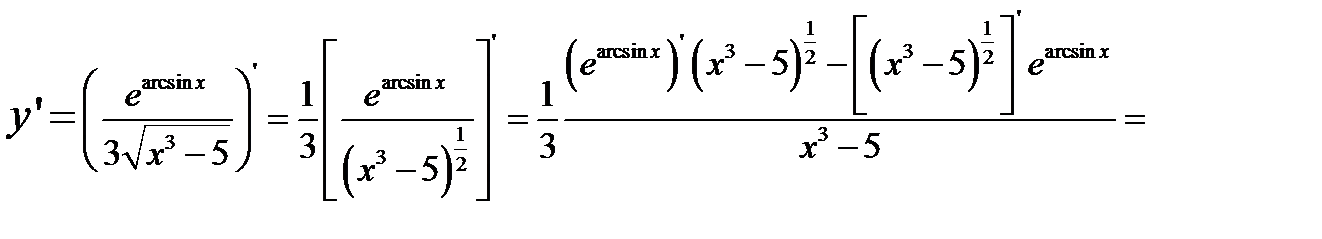
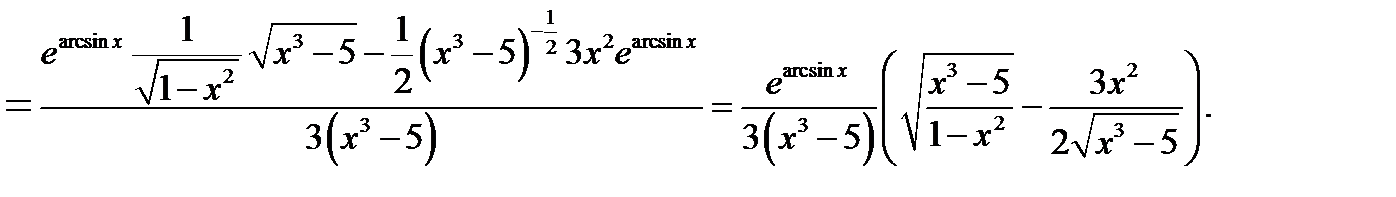
2) 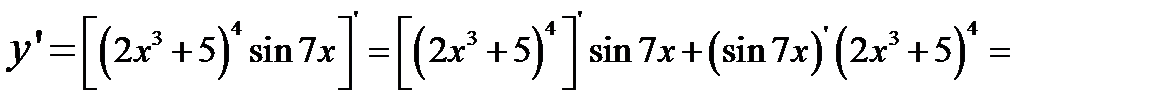
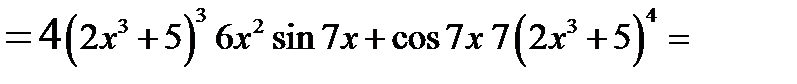
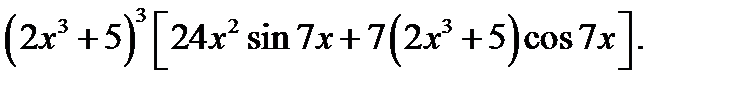
3) 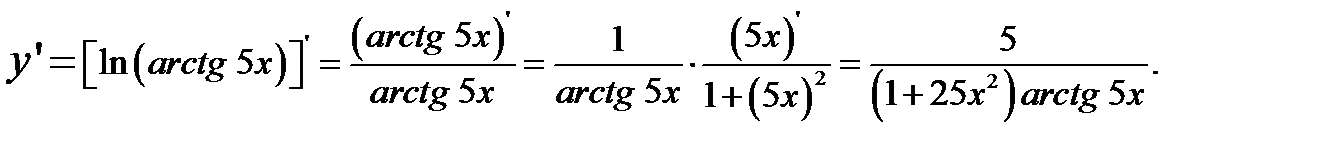
4) Здесь основание степени и показатель – переменные величины. Перейдем к основанию е: 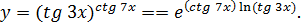 Тогда
Тогда 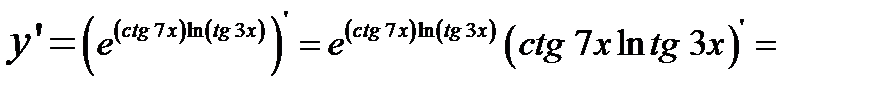
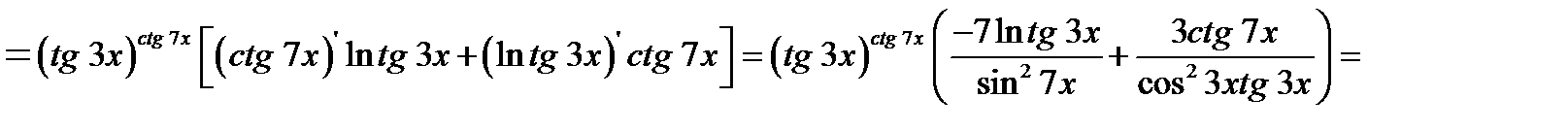
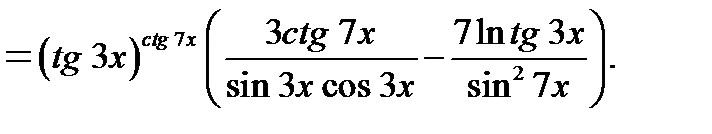
5) Данное уравнение задает в неявном виде функцию у. Найдем 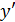 ,выполнив цепочку преобразований.
,выполнив цепочку преобразований.
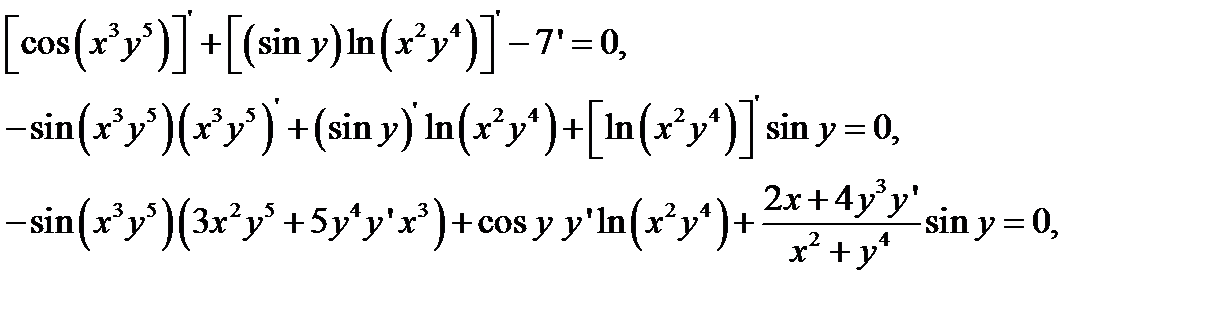
в левой части соберем члены, содержащие 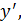
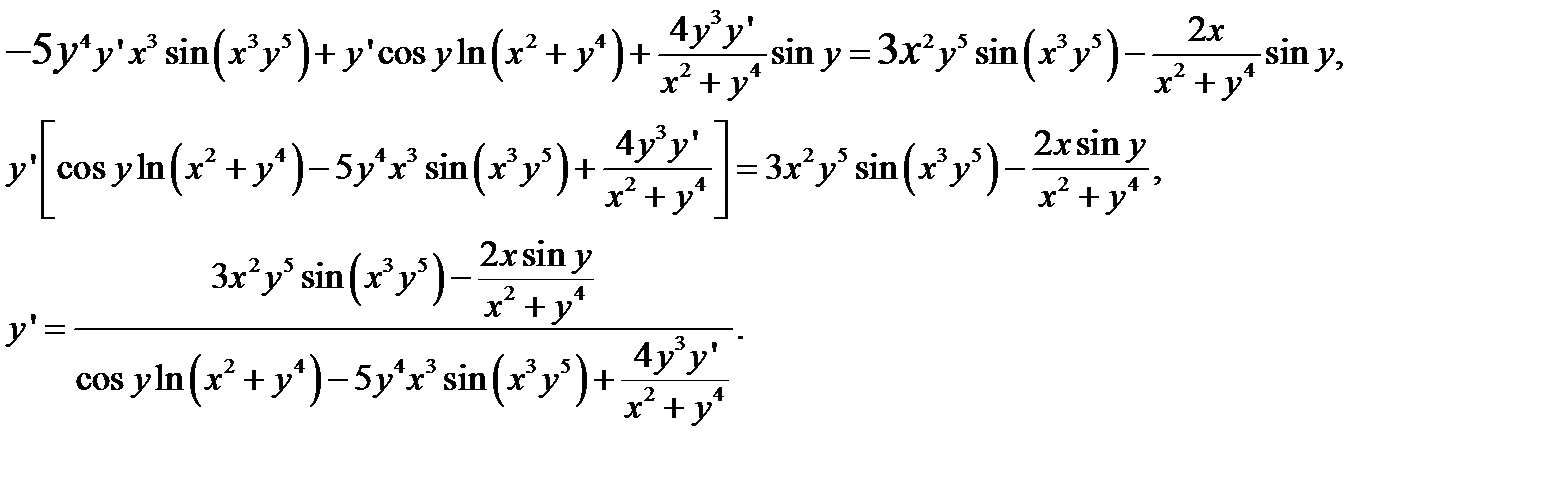
Образец выполнения заданий № 4
Задача.Найти 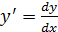 и
и 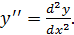
1) 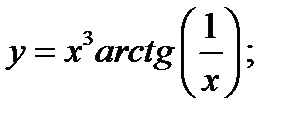 2)
2) 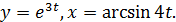
Решение.
1) 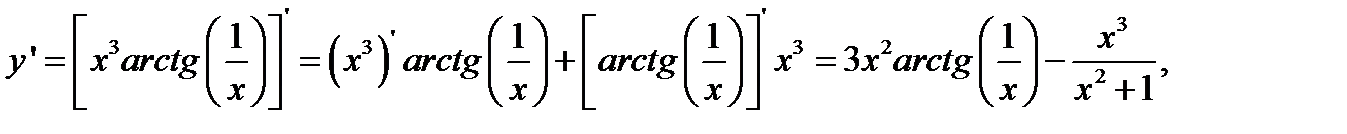
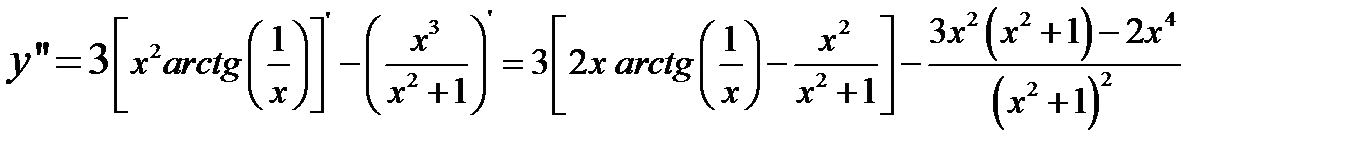 или
или
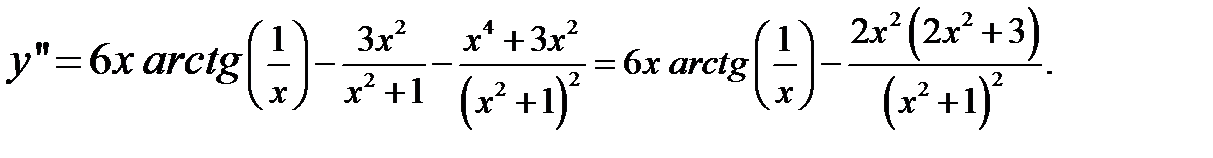
2) Здесь функции 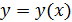 я задана параметрическими уравнениями.
я задана параметрическими уравнениями.
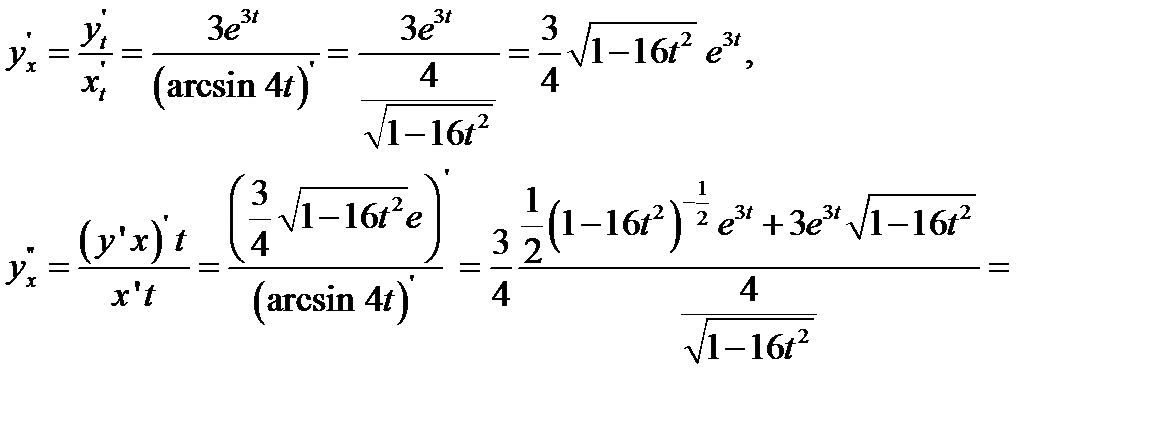
Образец выполнения заданий № 5
Задача.На какой высоте 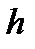 надо повесить фонарь над центром круговой площади радиуса
надо повесить фонарь над центром круговой площади радиуса 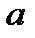 , чтобы площадка была максимально освещена у ее границы?
, чтобы площадка была максимально освещена у ее границы?
Решение.Из курса физики известно, что освещенность 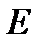 обратно пропорциональна квадрату расстояния от источника света и прямо пропорциональна косинусу угла падения (угла, образованного нормально к поверхности с направлением светового потока), т.е.
обратно пропорциональна квадрату расстояния от источника света и прямо пропорциональна косинусу угла падения (угла, образованного нормально к поверхности с направлением светового потока), т.е.
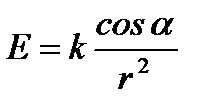 , где k зависит от силы источника света, помещенного в точке А (рис. 7). Из треугольника ОАВ имеем
, где k зависит от силы источника света, помещенного в точке А (рис. 7). Из треугольника ОАВ имеем 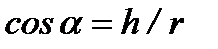 и
и 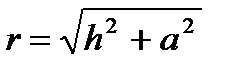 . Приняв h за независимую переменную, получим
. Приняв h за независимую переменную, получим 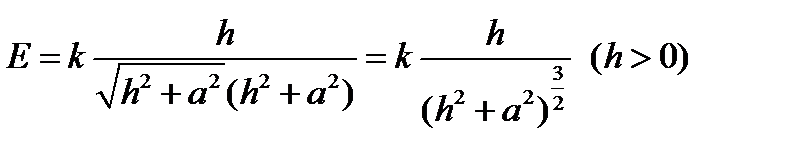 .
.
Исследуем функцию на экстремум с помощью первой производной:
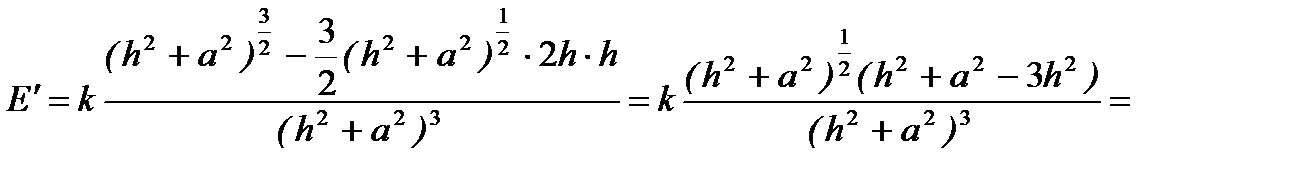
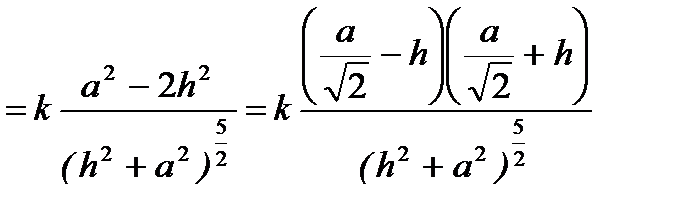 ;
; 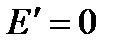 при
при 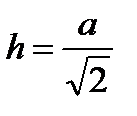 .
.
Так как 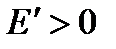 в промежутке
в промежутке 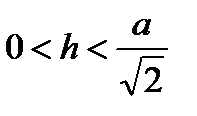 и
и 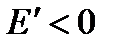 в промежутке
в промежутке 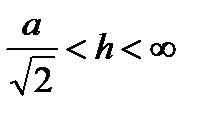 , то при
, то при 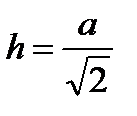 функция имеет максимум, т.е. при значении
функция имеет максимум, т.е. при значении 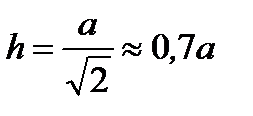 освещенность в точке В является наибольшей.
освещенность в точке В является наибольшей.
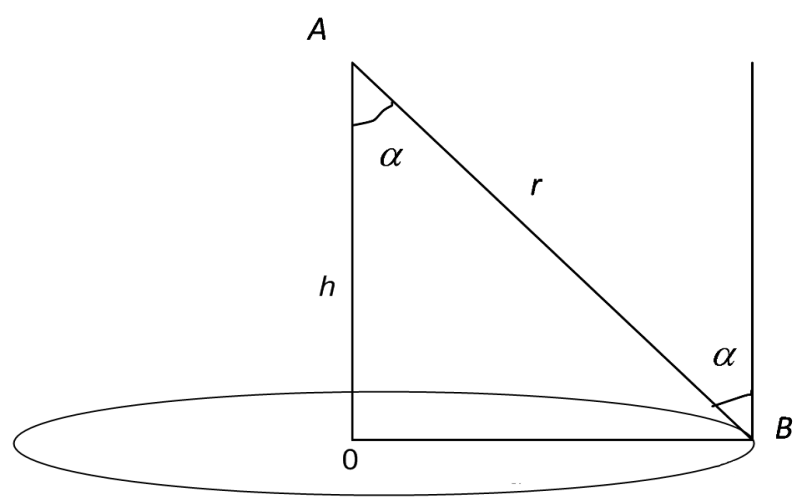
Рис. 7
Задания к контрольной работе №2
Задание № 1
Найти указанные пределы (не пользуясь правилом Лопиталя).
1. а) 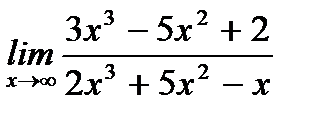 ;
;
б) 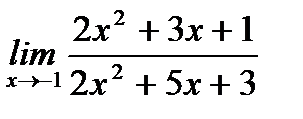 ;
;
в) 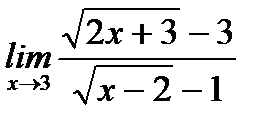 ;
;
г) 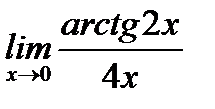 ;
;
д) 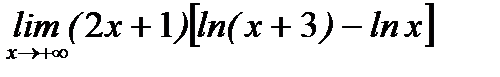 .
.
2. а) 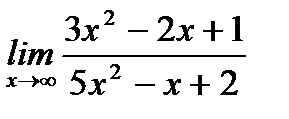 ;
;
б) 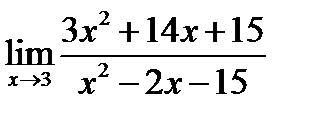 ;
;
в) 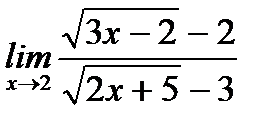 ;
;
г) 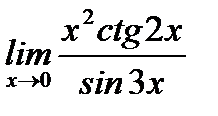 ;
;
д) 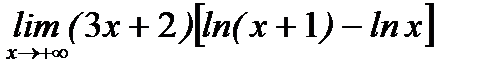 .
.
3. а) 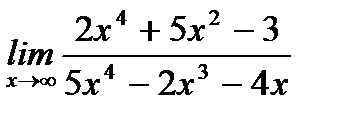 ;
;
б) 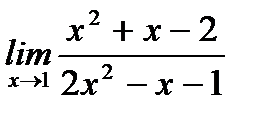 ;
;
в) 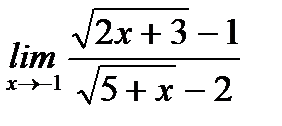 ;
;
г) 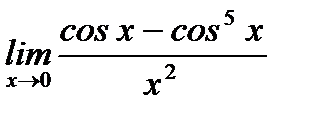 ;
;
д) 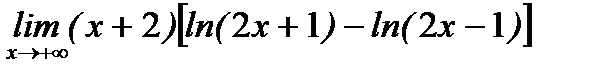 .
.
4. а) 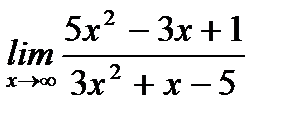 ;
;
б) 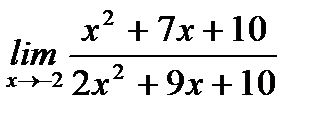 ;
;
в) 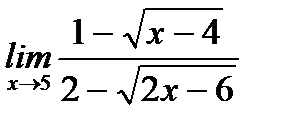 ;
;
г) 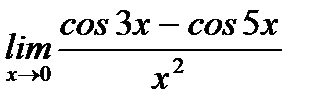 ;
;
д) 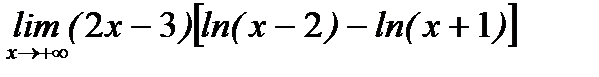 .
.
5. а) 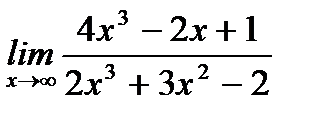 ;
;
б) 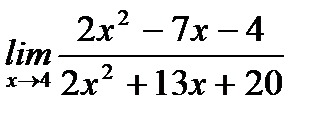 ;
;
в) 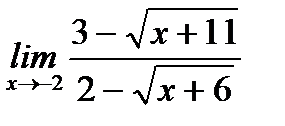 ;
;
г) 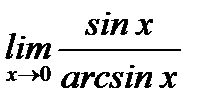 ;
;
д) 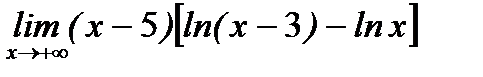 .
.
6. а) 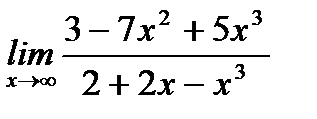 ;
;
б) 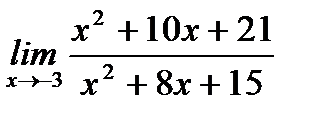 ;
;
в) 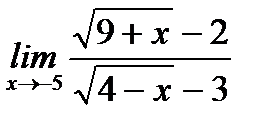 ;
;
г) 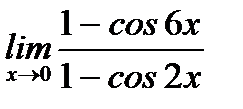 ;
;
д) 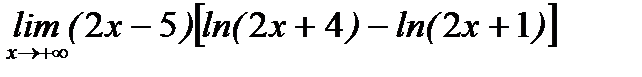 .
.
7. а) 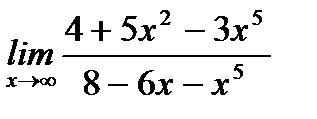 ;
;
б) 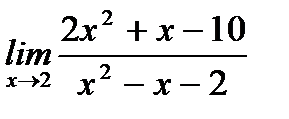 ;
;
в) 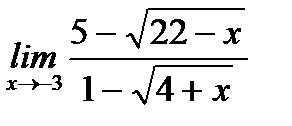 ;
;
г) 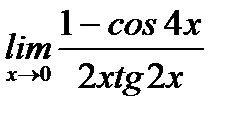 ;
;
д) 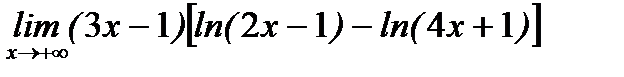 .
.
8. а) 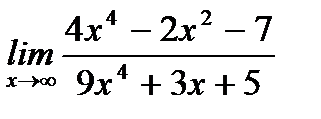 ;
;
б) 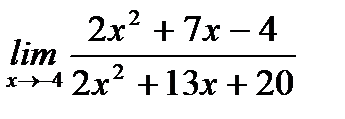 ;
;
в) 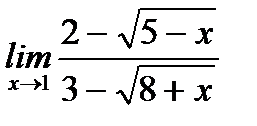 ;
;
г) 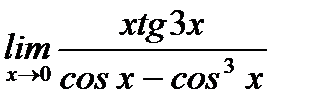 ;
;
д) 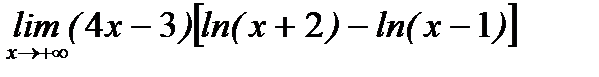 .
.
9. а) 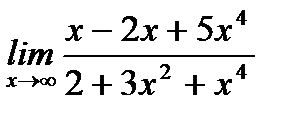 ;
;
б) 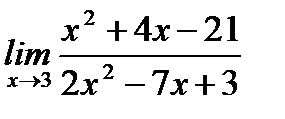 ;
;
в) 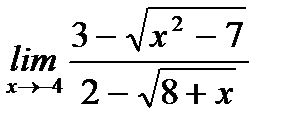 ;
;
г) 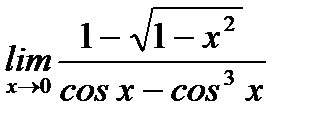 ;
;
д) 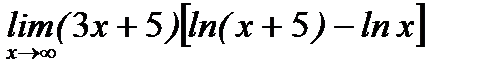 .
.
10. а) 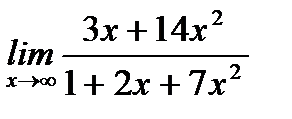 ;
;
б) 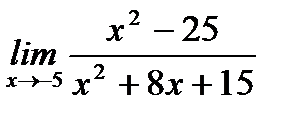 ;
;
в) 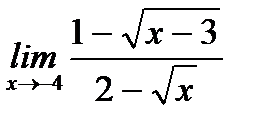 ;
;
г) 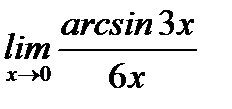 ;
;
д) 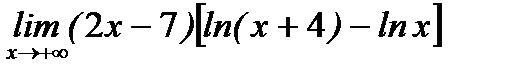 .
.
11. а) 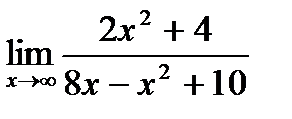 ;
;
б) 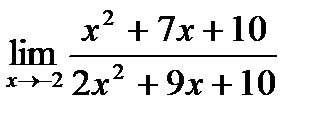 ;
;
в) 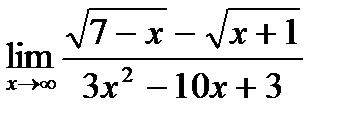 ;
;
г) 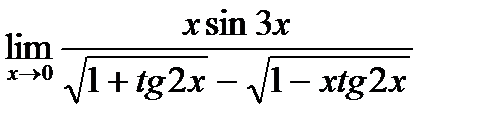 ;
;
д) 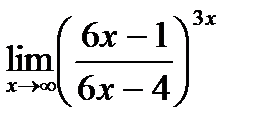 .
.
12. а) 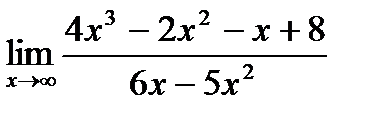 ;
;
б) 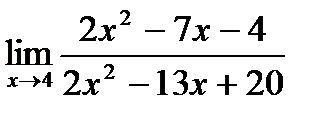 ;
;
в) 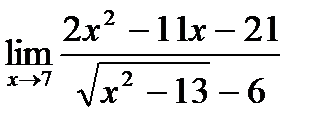 ;
;
г) 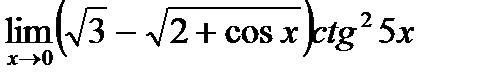 ;
;
д) 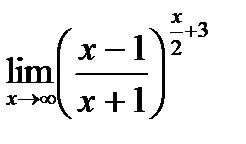 .
.
13. а) 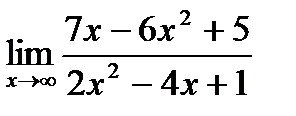 ;
;
б) 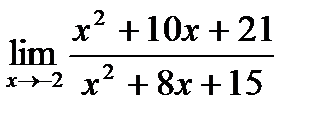 ;
;
в) 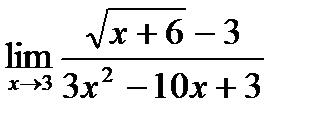 ;
;
г) 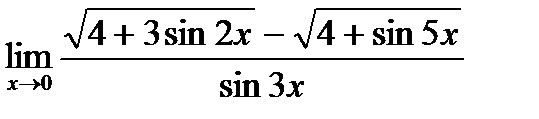 ;
;
д) 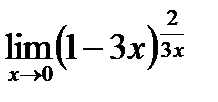 .
.
14. а) 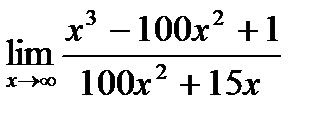 ;
;
б) 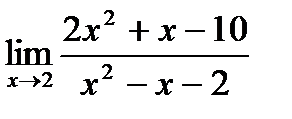 ;
;
в) 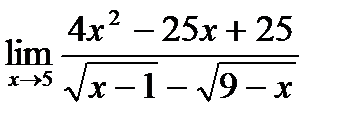 ;
;
г) 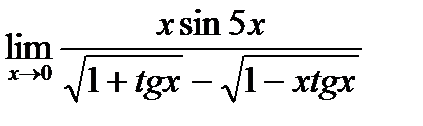 ;
;
д) 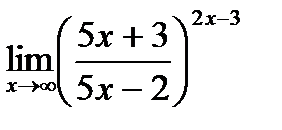 .
.
15. а) 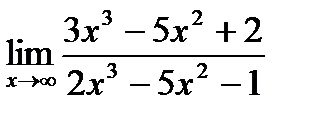 ;
;
б) 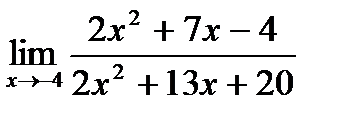 ;
;
в) 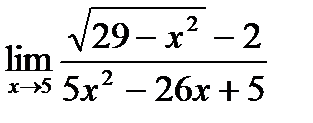 ;
;
г) 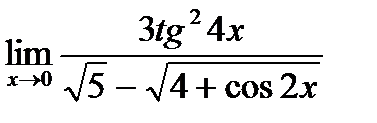 ;
;
д) 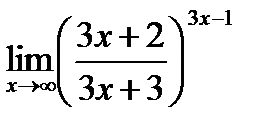 .
.
16. а) 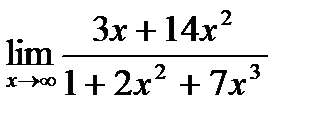 ;
;
б) 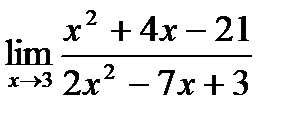 ;
;
в) 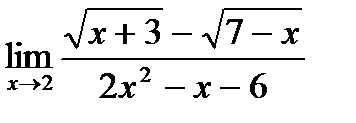 ;
;
г) 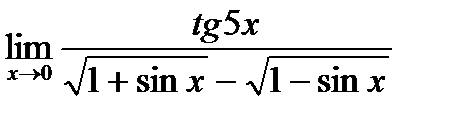 ;
;
д) 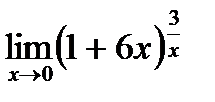 .
.
17. а) 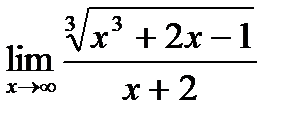 ;
;
б) 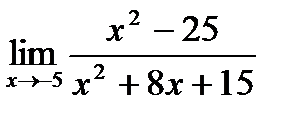 ;
;
в) 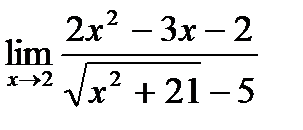 ;
;
г) 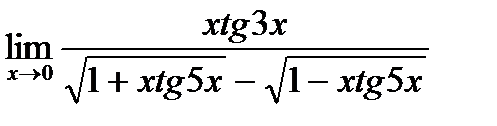 ;
;
д) 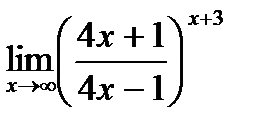 .
.
18. а) 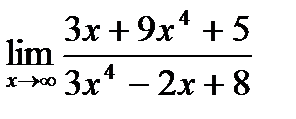 ;
;
б) 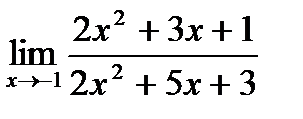 ;
;
в) 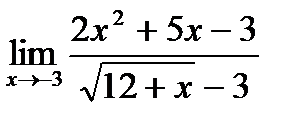 ;
;
г) 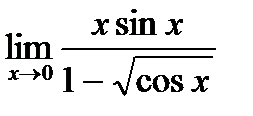 ;
;
д) 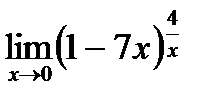 .
.
19. а) 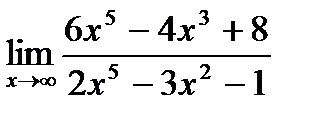 ;
;
б) 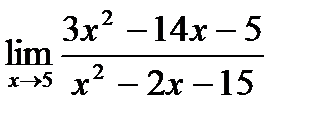 ;
;
в) 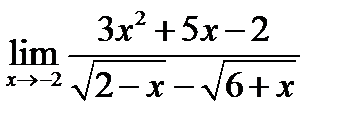 ;
;
г) 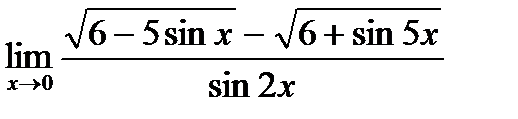 ;
;
д) 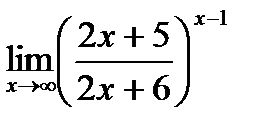 .
.
20. а) 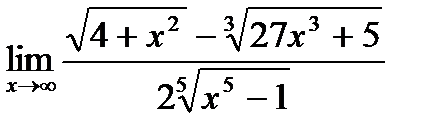 ;
;
б) 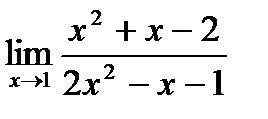 ;
;
в) 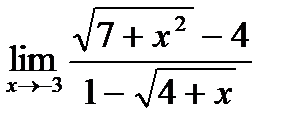 ;
;
г) 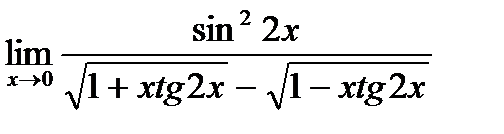 ;
;
д) 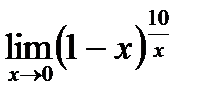 .
.
21. а) 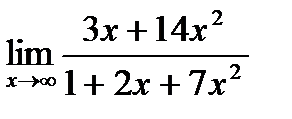 ;
;
б) 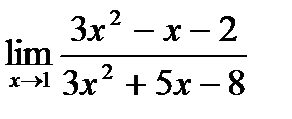 ;
;
в) 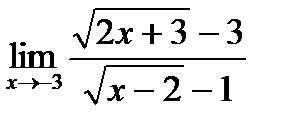 ;
;
г) 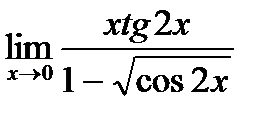 ;
;
д) 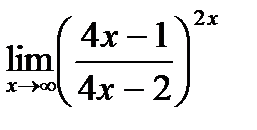 .
.
22. а) 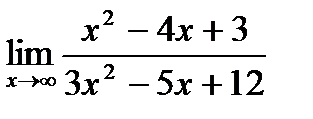 ;
;
б) 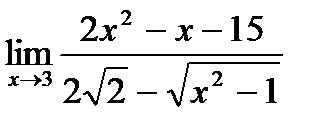 ;
;
в) 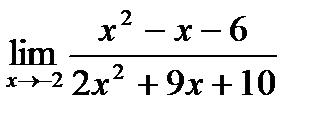 ;
;
г) 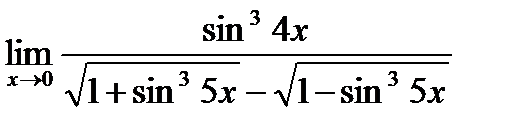 ;
;
д) 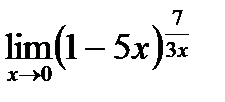 .
.
23. а) 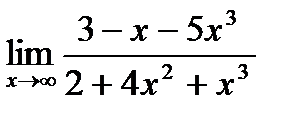 ;
;
б) 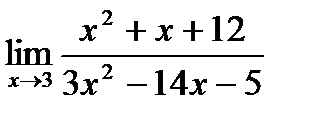 ;
;
в) 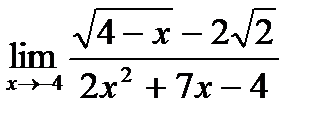 ;
;
г) 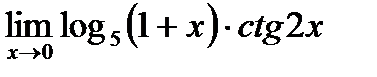 ;
;
д) 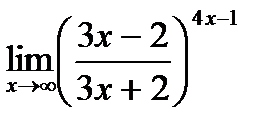 .
.
24. а) 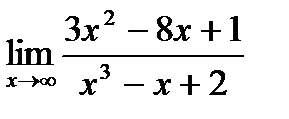 ;
;
б) 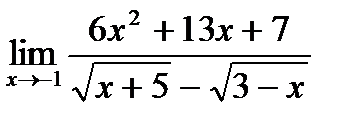 ;
;
в) 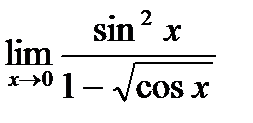 ;
;
г) 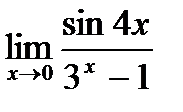 ;
;
д) 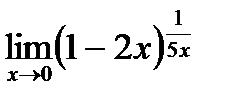 .
.
25. а) 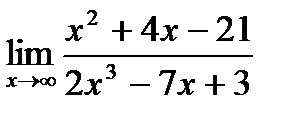 ;
;
б) 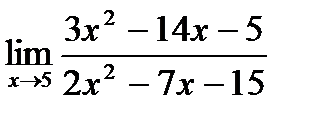 ;
;
в) 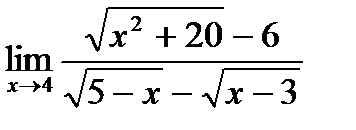 ;
;
г) 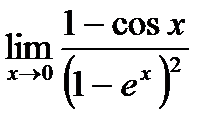 ;
;
д) 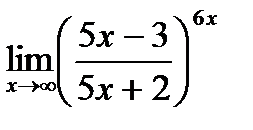 .
.
26. а) 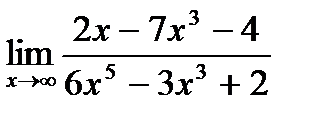 ;
;
б) 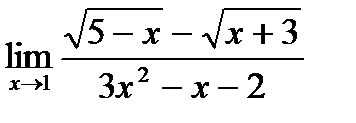 ;
;
в) 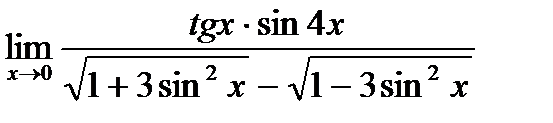 ;
;
г) 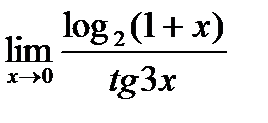 ;
;
д) 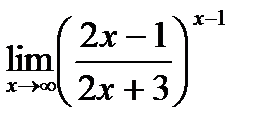 .
.
27. а) 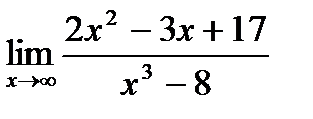 ;
;
б) 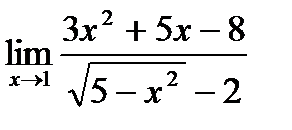 ;
;
в) 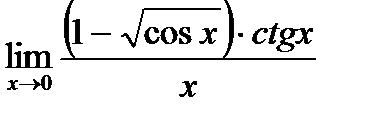 ;
;
г) 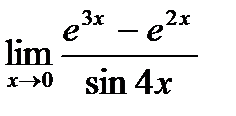 ;
;
д) 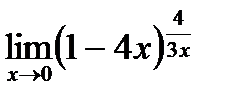 .
.
28. а) 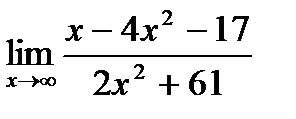 ;
;
б) 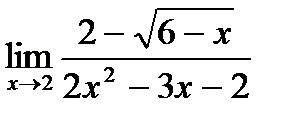 ;
;
в) 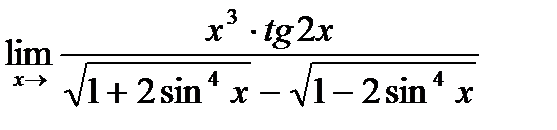 ;
;
г) 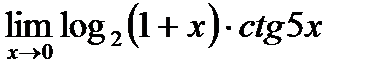 ;
;
д) 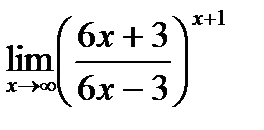 .
.
29. а) 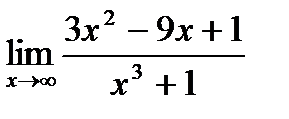 ;
;
б) 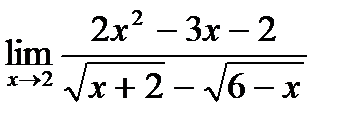 ;
;
в) 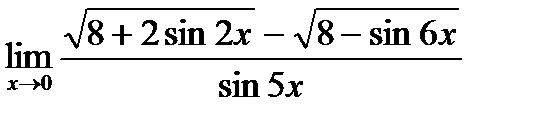 ;
;
г) 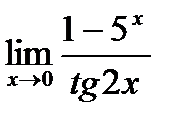 ;
;
д) 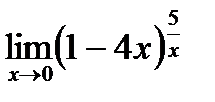 .
.
30. а) 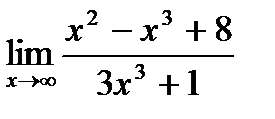 ;
;
б) 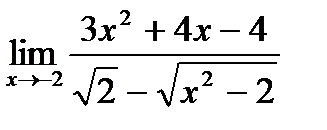 ;
;
в) 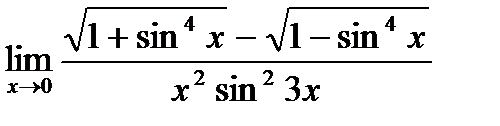 ;
;
г) 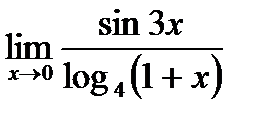 ;
;
д) 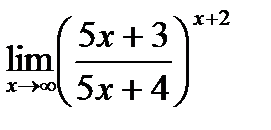 .
.
Задание № 2
В задачах 1-15 указываются функция и два значения аргумента 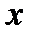 . Требуется: 1) найти предел функции при приближении к каждому из заданных значений
. Требуется: 1) найти предел функции при приближении к каждому из заданных значений 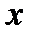 слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений
слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений 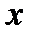 ; 3) сделать схематический чертеж.
; 3) сделать схематический чертеж.
В задачах 16-30 функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти скачок функции в каждой точке разрыва; 3) сделать схематический чертеж.
1. 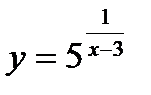 ;
; 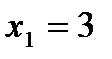 ,
, 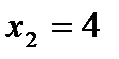
2. 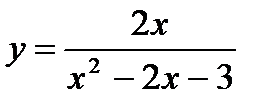 ;
; 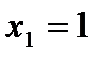 ,
, 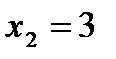
3. 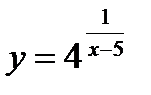 ;
; 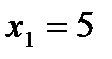 ,
, 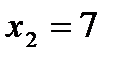
4. 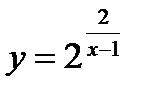 ;
; 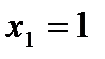 ,
, 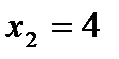
5. 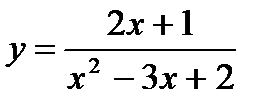 ;
; 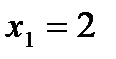 ,
, 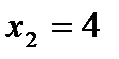
6. 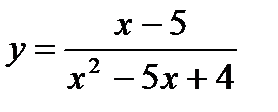 ;
; 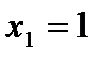 ,
, 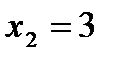
7. 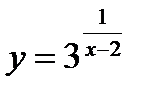 ;
; 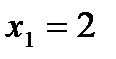 ,
, 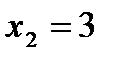
8. 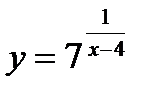 ;
; 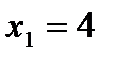 ,
, 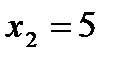
9. 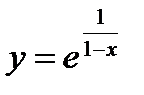 ;
; 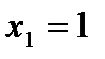 ,
, 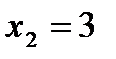
10. 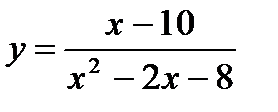 ;
; 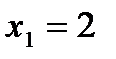 ,
, 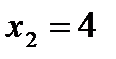
11. 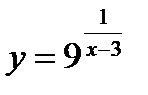 ;
; 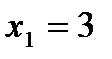 ,
, 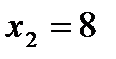
12. 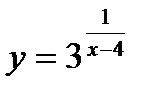 ;
; 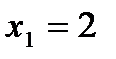 ,
, 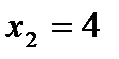
13. 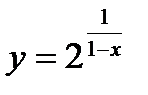 ;
; 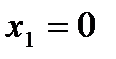 ,
, 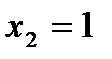
14. 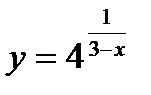 ;
; 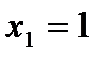 ,
, 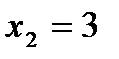
15. 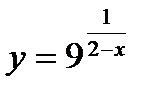 ;
; 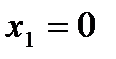 ,
, 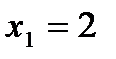 .
.
16. 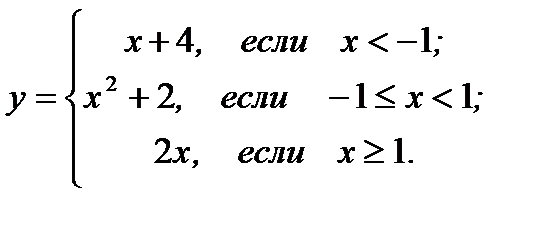
17. 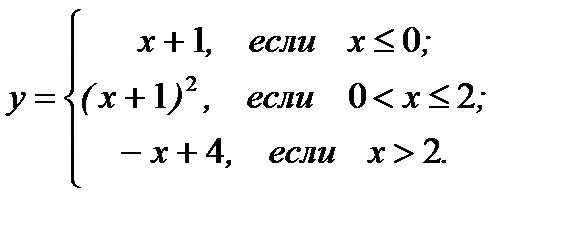
18. 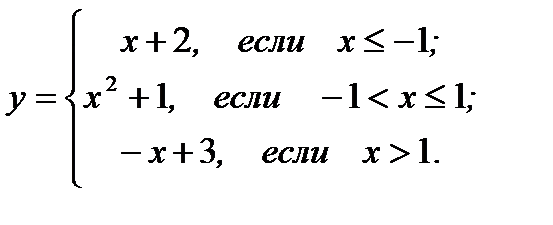
19. 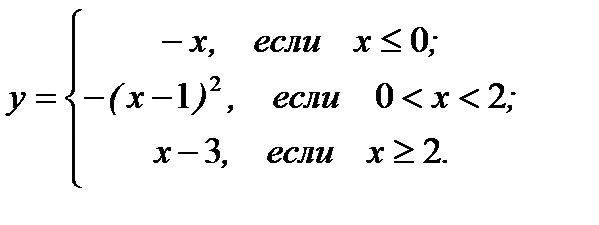
20. 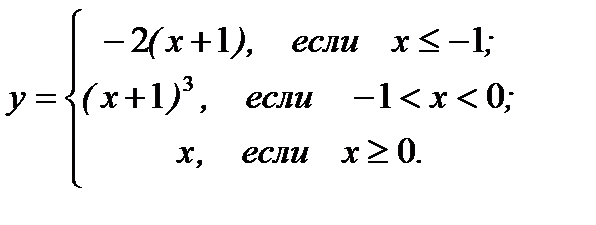
21. 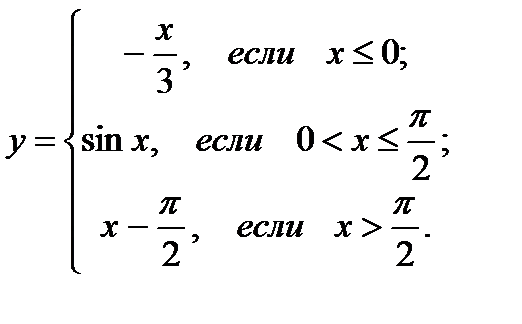
22. 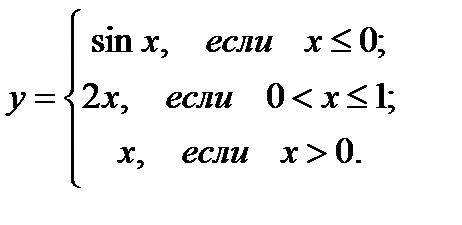
23. 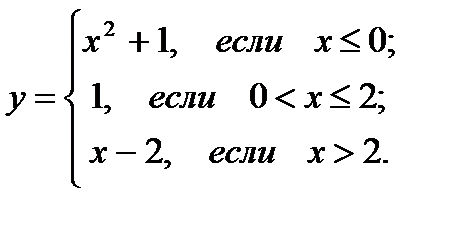
24. 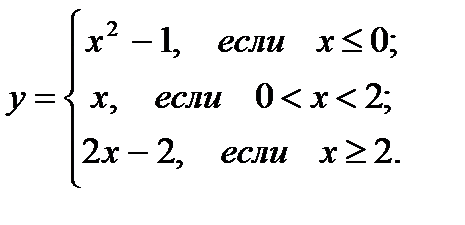
25. 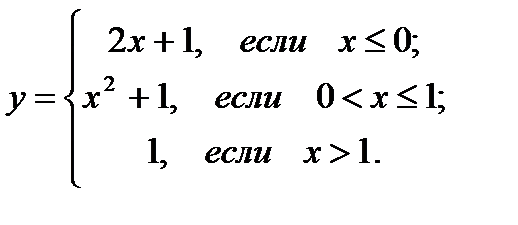
26. 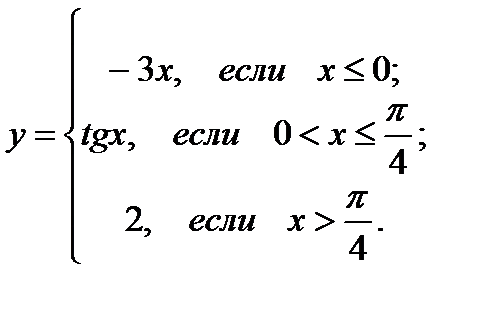
27. 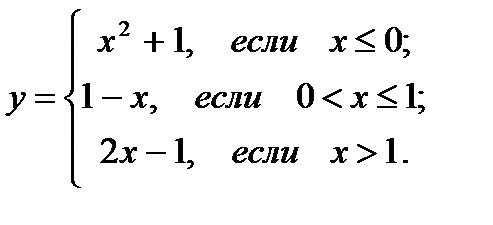
28. 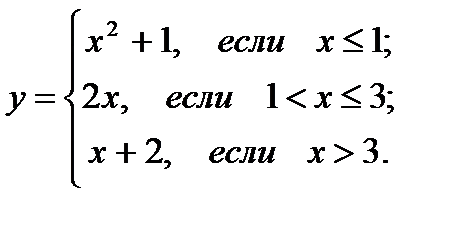
29. 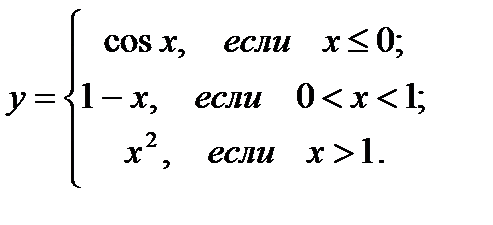
30. 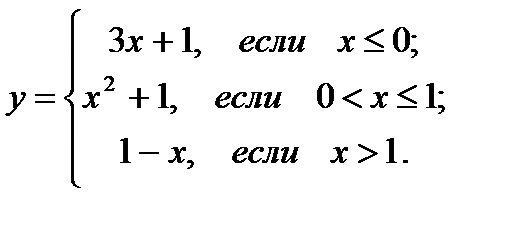
Задание № 3
Найти производные 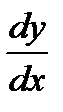 данных функций.
данных функций.
1. а) 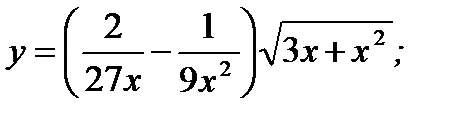
б) 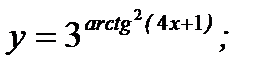
в) 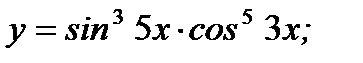
г) 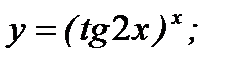
д) 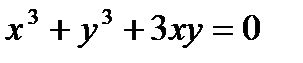 .
.
2. а) 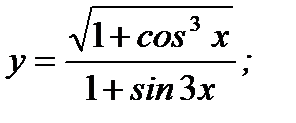
б) 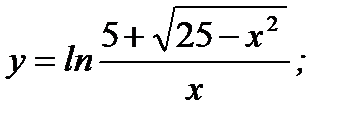
в) 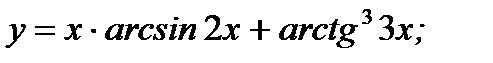
г) 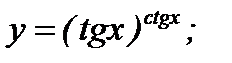
д) 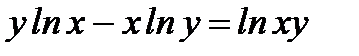 .
.
3. а) 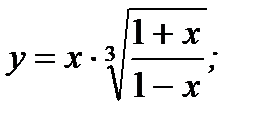
б) 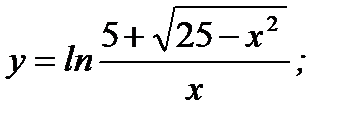
в) 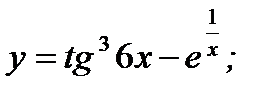
г) 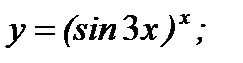
д) 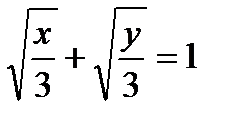 .
.
4. а) 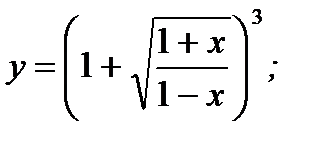
б) 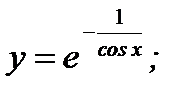
в) 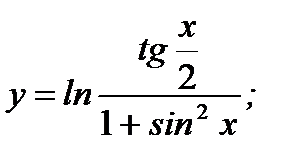
г) 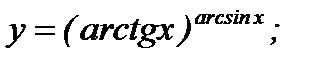
д) 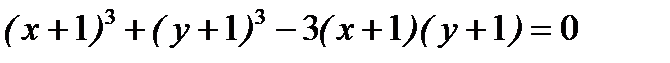 .
.
5. а) 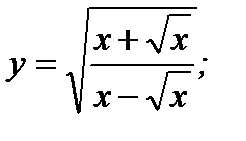
б) 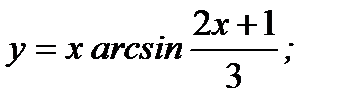
в) 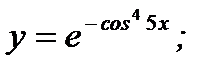
г) 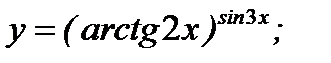
д) 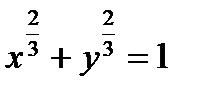 .
.
6. а) 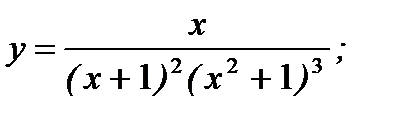
б) 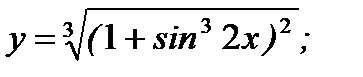
в) 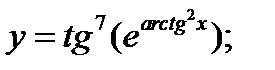
г) 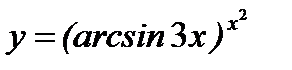 ;
;
д) 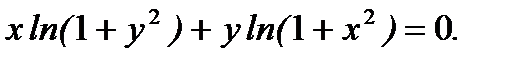
7. а) 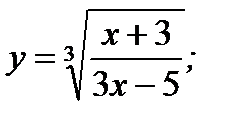
б) 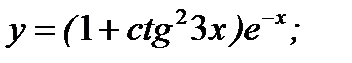
в) 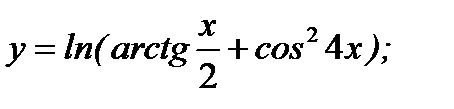
г) 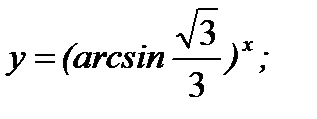
д) 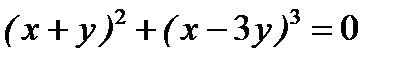 .
.
8. а) 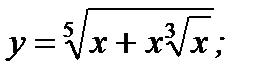
б) 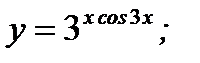
в) 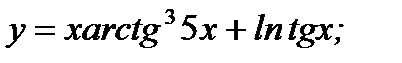
г) 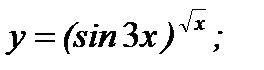
д) 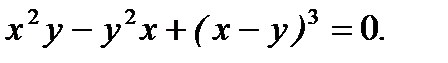
9. а) 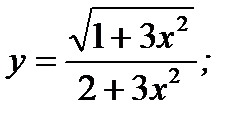
б) 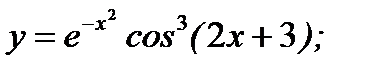
в) 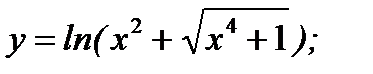
г) 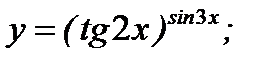
д) 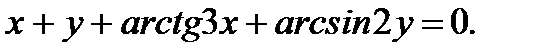
10. а) 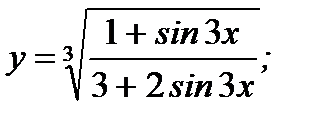
б) 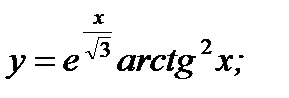
в) 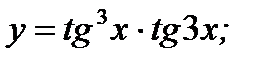
г) 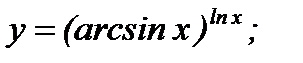
д) 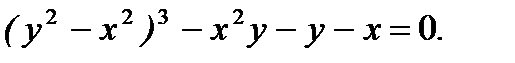
11. а) 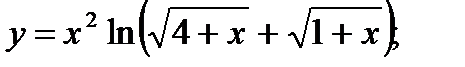
б) 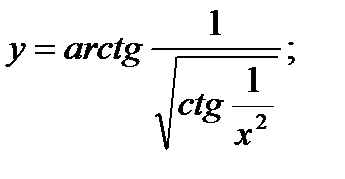
в) 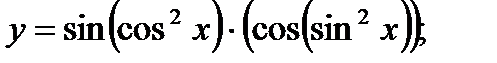
г) 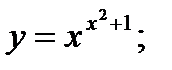
д) 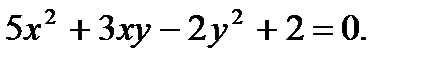
12. а) 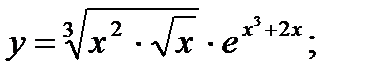
б) 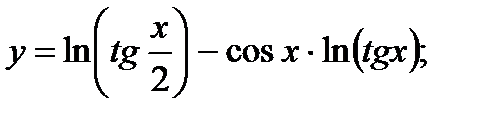
в) 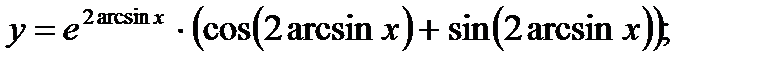
г) 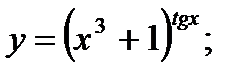
д) 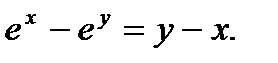
13. а) 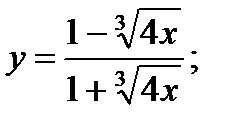
б) 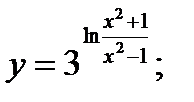
в) 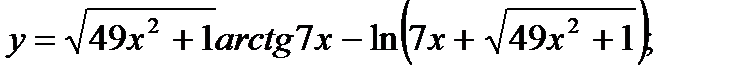
г) 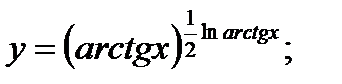
д) 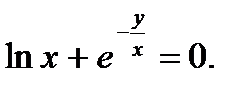
14. а) 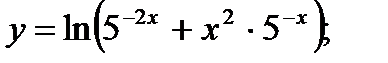
б) 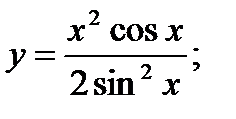
в) 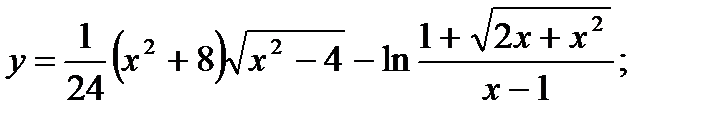
г) 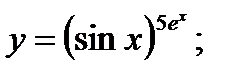
д) 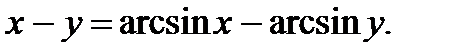
15. а) 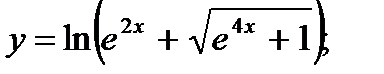
б) 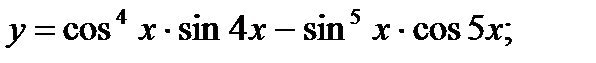
в) 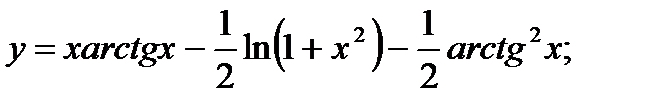
г) 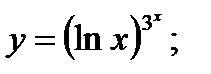
д) 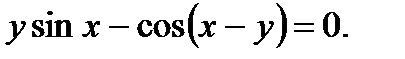
16. а) 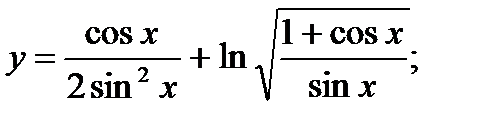
б) 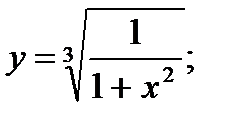
в) 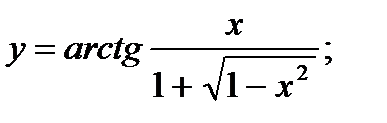
г) 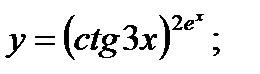
д) 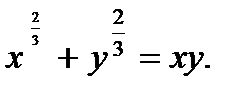
17. а) 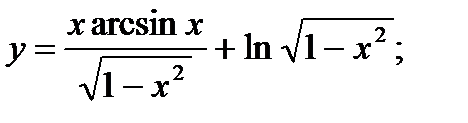
б) 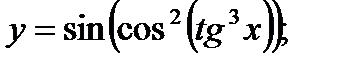
в) 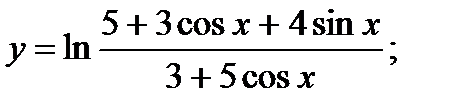
г) 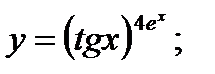
д) 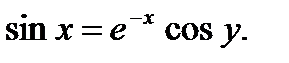
18. а) 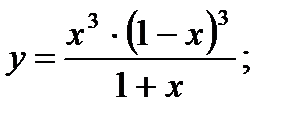
б) 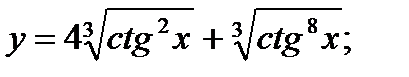
в) 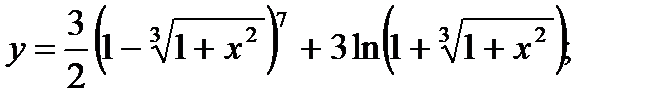
г) 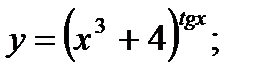
д) 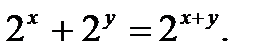
19. а) 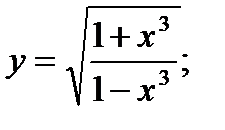
б) 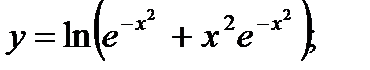
в) 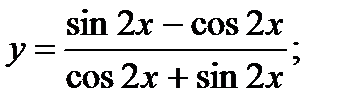
г) 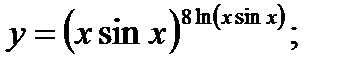
д) 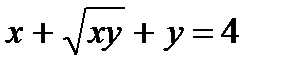 .
.
20. а) 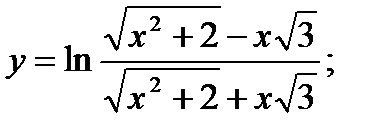
б) 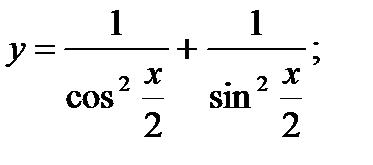
в) 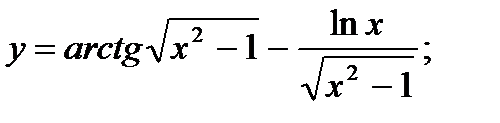
г) 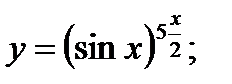
д) 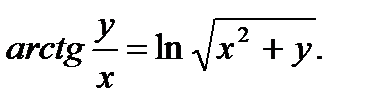
21. а) 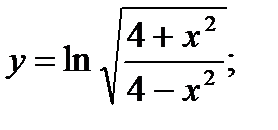
б) 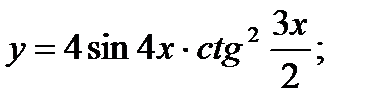
в) 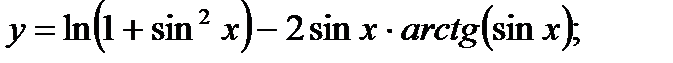
г) 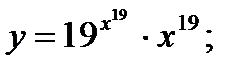
д) 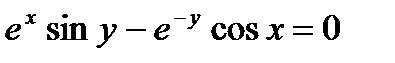 .
.
22. а) 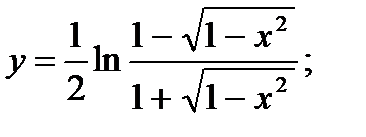
б) 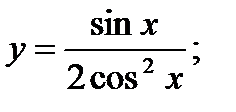
в) 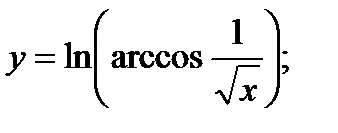
г) 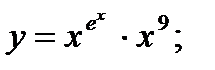
д) 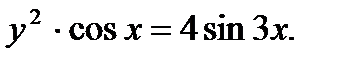
23. а) 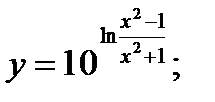
б) 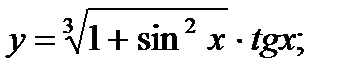
в) 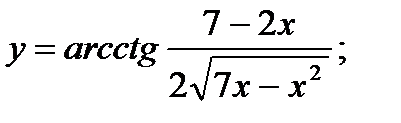
г) 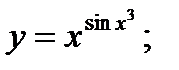
д) 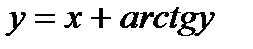
24. а) 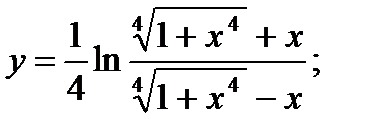
б) 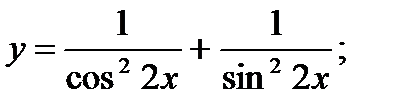
в) 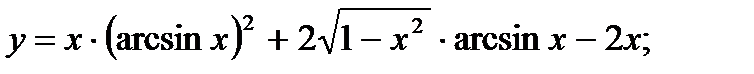
г) 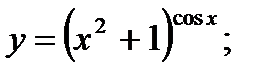
д) 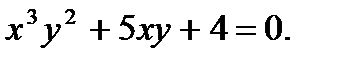
25. а) 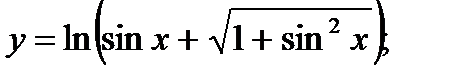
б) 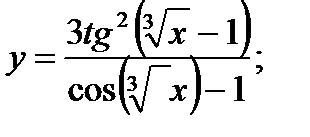
в) 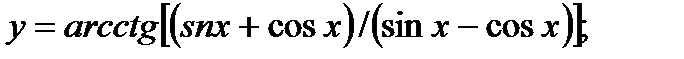
г) 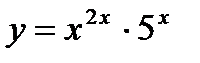 д)
д) 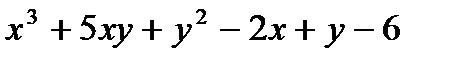
26. а) 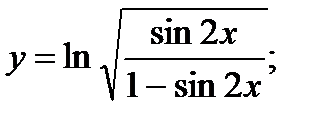
б) 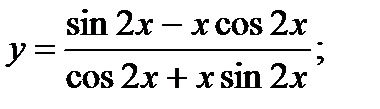
в) 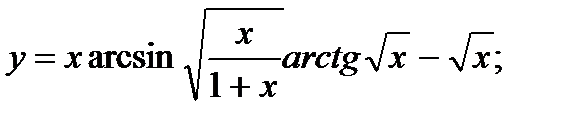
г) 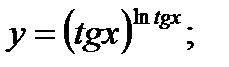
д) 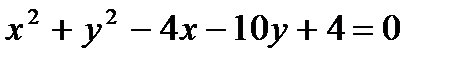
27. а) 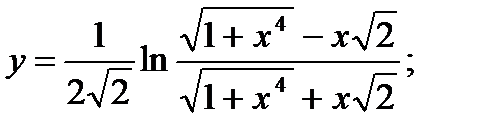
б) 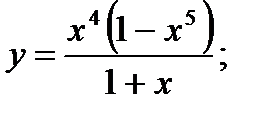
в) 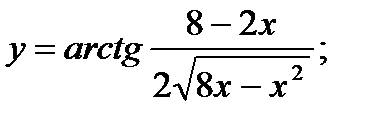
г) 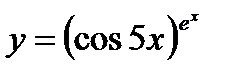
д) 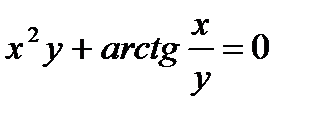
28. а) 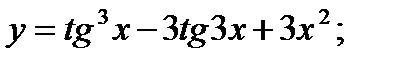
б) 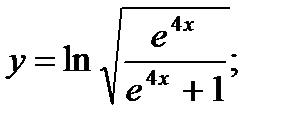
в) 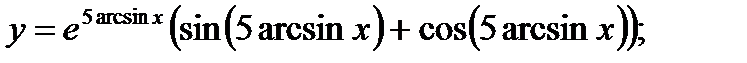
г) 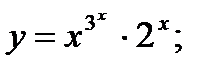
д) 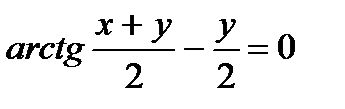
29. а) 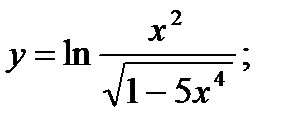
б) 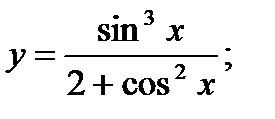
в) 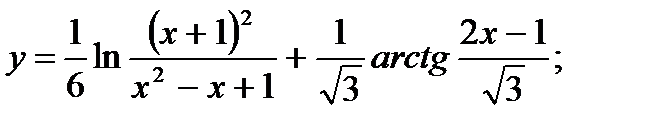
г) 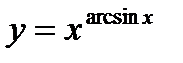 ;
;
д) 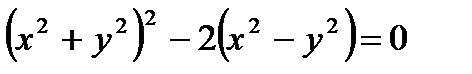 .
.
30. а) 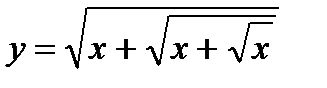 ;
;
б) 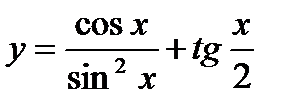 ;
;
в) 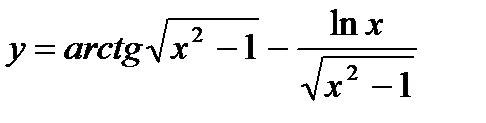
г) 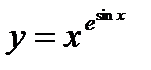 ;
;
д) 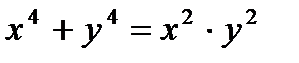 .
.
Задание № 4
Найти 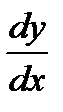 и
и 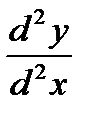 .
.
1. а) 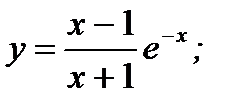
б) 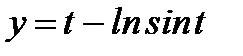 ,
, 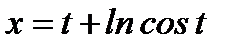 .
.
2. а) 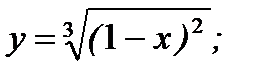
б) 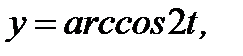
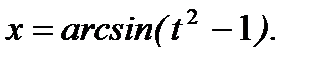
3. а) 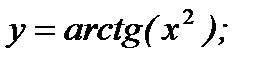
б) 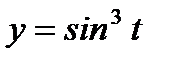 ,
, 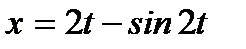 .
.
4. а) 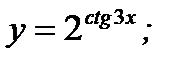
б) 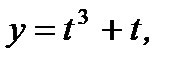
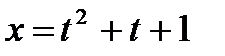 .
.
5. а) 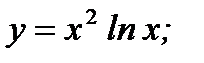
б) 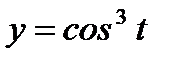 ,
, 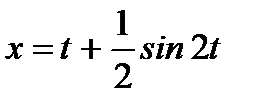 .
.
6. а) 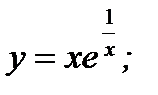
б) 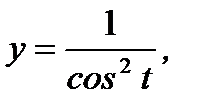
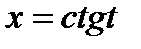 .
.
7. а) 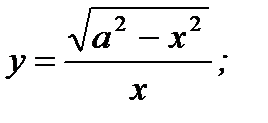
б) 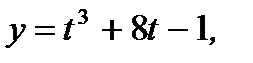
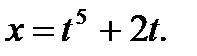
8. а) 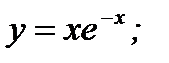
б) 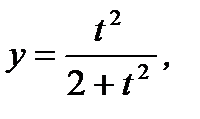
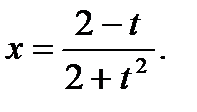
9. а) 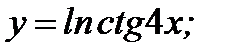
б) 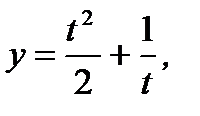
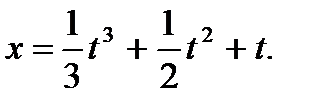
10. а) 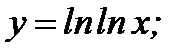
б) 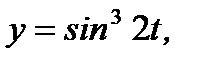
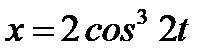 .
.
11. а) 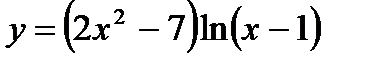
б) 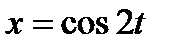 ,
, 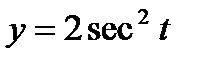 .
.
12. а) 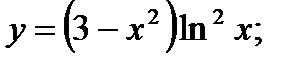
б) 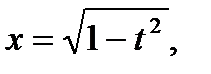
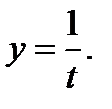
13. а) 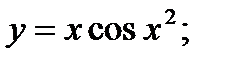
б) 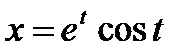 ,
, 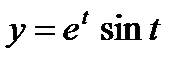 .
.
14. а) 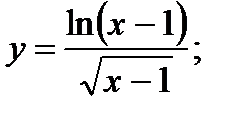
б) 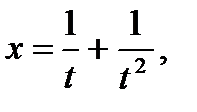
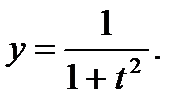
15. а) 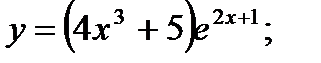
б) 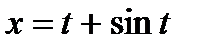 ,
, 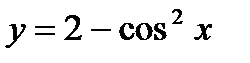 .
.
16. а) 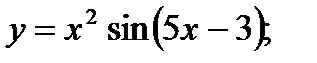
б) 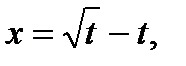
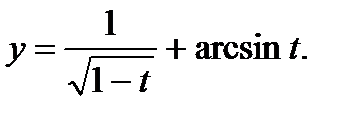
17. а) 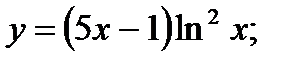
б) 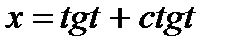 ,
, 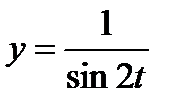 .
.
18. а) 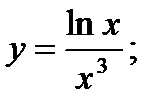
б) 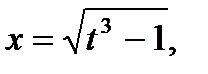
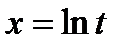
19. а) 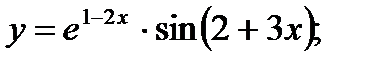
б) 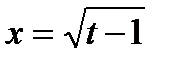 ,
, 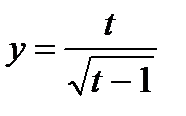 .
.
20. а) 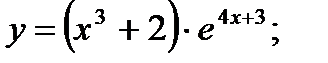
б) 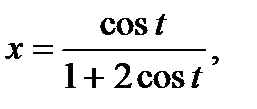
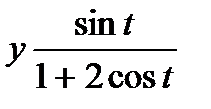
21. а) 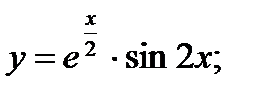
б) 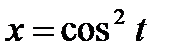 ,
, 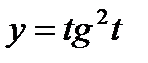 .
.
22. а) 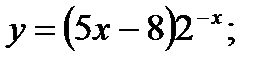
б) 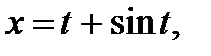
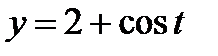
23. а) 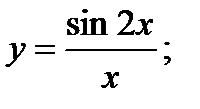
б) 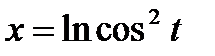 ,
, 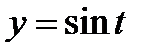 .
.
24. а) 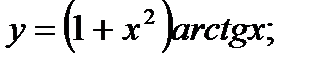
б) 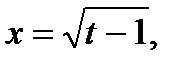
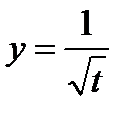
25. а) 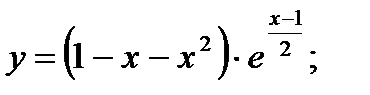
б) 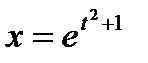 ,
, 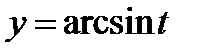 .
.
26. а) 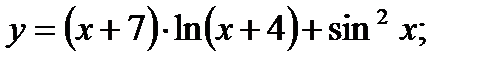
б) 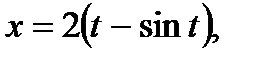
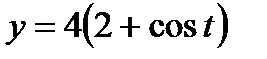
27. а) 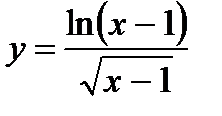
б) 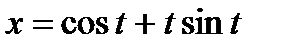 ,
, 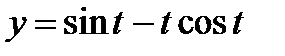 .
.
28. а)