Тема 14 Числовые характеристики случайных величин
Лекция 3.14.1 «Числовые характеристики случайных величин»
Учебные вопросы:
1. Характеристики положения
2. Характеристики рассеивания
Характеристики положения
Случайные величины, помимо законов распределения, могут также описываться числовыми характеристиками, среди которых различают характеристики положения (математическое ожидание, мода, медиана и др.) и характеристики рассеивания (дисперсия, среднеквадратичное отклонение, различные моменты распределения порядка выше первого и др.).
Математическим ожиданием (средним значением по распределению,средним) называется действительное число, определяемое в зависимости от типа случайной величины X формулой
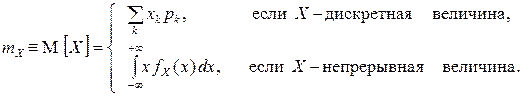 (1)
(1)
Из определения математического ожидания легко получаются следующие его свойства:
a. Аддитивность 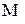 [X + Y] =
[X + Y] = 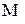 [X] +
[X] + 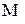 [Y], т. е. математическое ожидание суммы случайных величин равно сумме математическихожиданий слагаемых. Это свойство распространяется на случай любого конечного числа слагаемых;
[Y], т. е. математическое ожидание суммы случайных величин равно сумме математическихожиданий слагаемых. Это свойство распространяется на случай любого конечного числа слагаемых;
b. Для любого числа 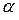
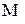 [
[ 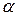 X] =
X] = 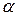
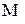 [X],
[X],
т. е. постоянный множитель 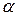 можно выносить за знакматематического ожидания;
можно выносить за знакматематического ожидания;
c. Математическое ожидание индикатора 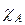 события А равно вероятности этого события:
события А равно вероятности этого события:
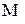 [
[ 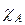 ] =
] =  (А);
(А);
d. Свойство монотонности: если Х ≥ Y, то
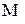 [X] ≥
[X] ≥ 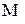 [Y];
[Y];
e. Для независимых случайных величин X и Y имеет место мультипликативное свойство математического ожидания:
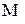 [X∙Y] =
[X∙Y] = 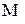 [X] ∙
[X] ∙ 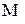 [Y],
[Y],
т. е. математическое ожидание произведения независимых случайных величин равно произведениюих математических ожиданий. Свойство мультипликативности распространяется на случай произвольного конечного числа независимых случайных величин. Следует отметить, что если свойство аддитивности математического ожидания справедливо для любых случайных величин, то свойство мультипликативности математического ожидания справедливо только для независимых случайных величин.
Модой случайной величины X непрерывного типа называется такое ее числовое значение 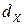 , для которого плотность распределения вероятностей
, для которого плотность распределения вероятностей 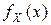 этой величины имеет максимум. Мода случайной величины дискретного типа определяется как такое ее возможное значение
этой величины имеет максимум. Мода случайной величины дискретного типа определяется как такое ее возможное значение 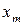 , для которого
, для которого
 {X =
{X = 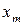 } = max
} = max  {X =
{X = 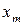 }. (2)
}. (2)
k
Таким образом, мода дискретной случайной величины есть ее наиболее вероятное значение в случае, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальноераспределение).
Медианой случайной величины X непрерывного типа называется такое ее числовое значение 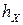 , при котором
, при котором
 {Х <
{Х < 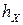 } =
} =  {Х ≥
{Х ≥ 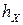 } или FХ (x) =
} или FХ (x) = 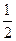 . (3)
. (3)
Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
