Плоскости и в пространстве

[2],гл.4; [8],гл.3,§2;[10]

В декартовой системе координат на плоскости всякому уравнению первой степени относительно текущих координат соответствует прямая линия, а уравнению второй степени соответствует в общем случае кривая второго порядка - эллипс (окружность), гипербола или парабола. (Возможны и вырожденные случаи: например, уравнению 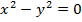соответствуют две пересекающиеся прямые х – у =0 и х + у =0, а 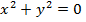точка x = , у = 0).

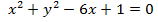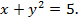Пример 7. Найти координаты точек пересечения кривых и Указать вид кривых. Сделать чертеж.

Решение: Определим вид кривых. Уравнение 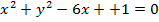определяет окружность с центром в точке (3; 0) и радиусом .

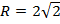Уравнению 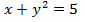или 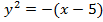соответствует парабола, симметричная относительно оси Ох, ветви которой направлены влево, а вершина находится в точке (5,0). Координаты точек пересечения двух заданных линий являются решениями системы уравнений:

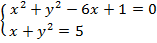
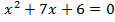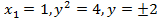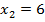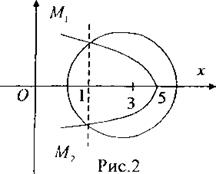
Подставляя у = 5 – х из второго уравнения в первое, получим , откуда . Тогда при уравнение 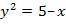решения не имеет. Таким образом, заданные окружность и парабола пересекаются в двух точках 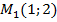и 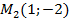(см.рис.2).

В декартовой системе координат в пространстве всякому уравнению первой степени относительно текущих координат соответствует плоскость, а уравнению второй степени в общем случае соответствует поверхности п. второго порядка (за исключением вырожденных случаев).

Пример 8. Тело в пространстве задано системой неравенств

Определить вид поверхностей, его ограничивающих, и изобразить это

	Рис.3		Рис.4		Рис.5

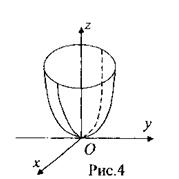
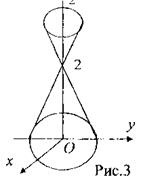
Решение: Уравнение 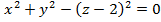задаёт в прострации конус с осью Оz, смещенный вдоль оси Оz на 2 (рис.З). Он разбивает все пространство на три части. Объединение двух из них, содержащих точки оси Оz, задается неравенством 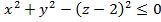. Параболоид,

задаваемый уравнением 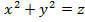(рис.4), разбивает пространство на две части, одна из которых и задается неравенством 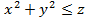. Так как координаты точки А(0; 0; 2) удовлетворяют этому неравенству, то речь, очевидно, идет о части пространства, лежащей внутри параболоида.

Наконец, 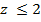задает то полупространство, которое лежит ниже плоскости 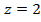. Поверхност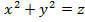и и 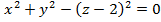пересекаются в плоскости z=1 по окружности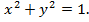

Объединяя эти результаты, мы получим, что исследуемое тело имеет вид, указанный на рис.5.

Пример 9. Сделать схематический рисунок тела, заданного системой неравенств

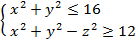
Указать вид поверхностей, ограничивающих тело. Определить, по каким линиям и в каких плоскостях пересекаются эти поверхности.

		Рис. 7		Рис. 8
	Рис. 6

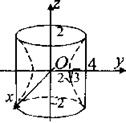
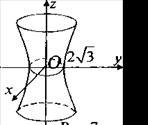
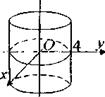
Решение: Уравнение х + у = 16 задает цилиндр с осью От, направляющей которого является окружность радиуса 4 с центром в начале координат (рис.6). Уравнение задает однополостный гиперболоид (ось вращения - ось Оz), радиус "горла" (сечение плоскостью z = 0) равен 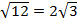(рис.7). Очевидно, что линиями пересечения поверхностей будут окружности того же радиуса, что и направляющая цилиндра. Определим, в каких плоскостях пересекаются поверхности. Для этого из уравнений системы исключим x и 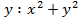подставим в уравнение гиперболоида. Получим 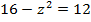или 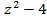, откуда .

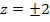На рис.8 изображено тело, ограниченное снаружи цилиндром, а изнутри однополостным гиперболоидом, которые пересекаются по двум окружностям с центрами на оси Оz , с одинаковыми радиусами R = 4, расположенными в плоскостях z = 2 и z = –2.