Однородные дифференциальные уравнения.

ЗАДАНИЕ N 38 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Общий интеграл дифференциального уравнения имеет вид …

			, где
			где
			где
			где

Решение:
Сделаем замену Тогда 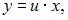и уравнение примет вид: После преобразований получим уравнение с разделяющимися переменными
или Проинтегрировав обе части, получим: где . Сделаем обратную замену:

ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Общий интеграл дифференциального уравнения имеет вид …

Решение:
Запишем уравнение в виде Сделаем замену
Тогда 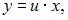и уравнение запишется в виде
Разделим переменные: и проинтегрируем обе части последнего уравнения:
Сделаем обратную замену:

ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Дифференциальное уравнение заменой приводится к уравнению с разделенными переменными,
которое имеет вид …

ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Дифференциальное уравнение заменой приводится к уравнению с разделенными переменными,
которое имеет вид …

Решение:
Если то и
Тогда уравнение запишется в виде
Разделив переменные, получим:

ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Общее решение дифференциального уравнения имеет вид …

			, где
			где
			где
			где

Решение:
Запишем уравнение в виде Сделаем замену
Тогда 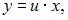и уравнение примет вид:
Разделив переменные, получим:
Проинтегрируем обе части последнего уравнения: где
Тогда Сделаем обратную замену:

ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Общий интеграл дифференциального уравнения имеет вид …

Решение:
Сделаем замену Тогда 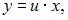и уравнение примет вид:
Проинтегрировав обе части, получим:
Сделаем обратную замену:

ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Интегральные кривые уравнения имеют вид …

Решение:
Данное уравнение является однородным дифференциальным уравнением первого порядка. Сделаем замену тогда и Уравнение запишется в виде: Сократив на и разделив переменные, получим: Проинтегрируем обе части: или где . Сделаем обратную замену:

ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Однородные дифференциальные уравнения
Дифференциальное уравнение заменой приводится
к уравнению с разделенными переменными, которое имеет вид …

Решение:
Если то и
Тогда уравнение
запишется в виде
После сокращения на x⁴ и упрощения, получим: