Метод Рунге - Кутта 4-го порядка

Самое большое распространение из всех численных методов решения дифференциальных уравнений получил метод Рунге-Кутта 4-го порядка. В этом методе на каждом шаге интегрирования дифференциальных уравнений искомая функция y(x) аппроксимируется рядом Тейлора, содержащим члены ряда с h⁴:

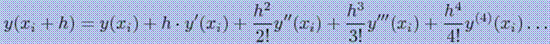
В результате ошибка на каждом шаге имеет порядок h⁵.

Для сохранения членов ряда, содержащих h₂,h₃,h₄ необходимо определить вторую y", третью y"' и четвертую y⁽⁴⁾производные функции y(x). Эти производные аппроксимируем разделенными разностями второго, третьего и четвертого порядков соответственно.

В результате для получения значения функции y_i+1 по методу Рунге-Кутта выполняется следующая последовательность вычислительных операций:

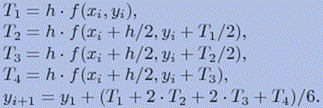
Перейдем к реализации метода Рунге-Кутта на основе нашего класса .

public abstract class TRungeKutta : TODE

{double[] Yl, Y2, Y3, Y4; // внутренние переменные

public TRungeKutta(int N) : base(N)

{ Yl = new double[N]; Y2 = new double[N]; Y3 = new double[N]; Y4 = new double[N];}

// следующий шаг метода Рунге-Кутта, dt - шаг по времени

override public void NextStep(double dt)

{if (dt < 0) {return; }

int i;

F(T, Y, ref Yl); // рассчитать Yl

for (i = 0; i < N; i++)

{ YY[i] = Y[i] + Yl[i] * (dt / 2.0);

F(T + dt / 2.0, YY, ref Y2); // рассчитать Y2

for (i = 0; i < N; i++) {

YY[i] = Y[i] + Y2[i] * (dt / 2.0);

F(T + dt / 2.0, YY, ref Y3); // рассчитать Y3

for (i = 0; i < N; i++) { YY[i] = Y[i] + Y3[i] * dt;

F(T + dt, YY, ref Y4); // рассчитать Y4

for (i = 0; i < N; i++) {

// рассчитать решение на новом шаге

Y[i] = Y[i] + dt / 6.0 * (Yl[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]);}

T = T + dt; // увеличить шаг

} } } } }

Теперь протестируем наши методы на примере задач Коши, описывающей гармонические колебания математического маятника. Мы решаем следующую задачу.

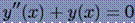
с начальными условиями

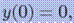
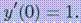
Эта задача имеет единственное решение - 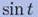. Чтобы применить к этой задаче наши методы нужно записать ее в виде системы уравнений первого порядка.

После такой замены мы имеет следующую систему

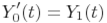
с начальными условиями

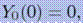
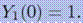
Реализуем для нашей системы методы Эйлера и Рунге-Кутты

public class SystEuler : TEuler

{public SystEuler() : base(2) { }

public override void F(double t, double[] Y, ref double[] FY)

{FY[0] = Y[1]; FY[1] = -Y[0]; } }

public class SystRK : TRungeKutta {public SystRK() : base(2) {}

public override void F(double t, double [] Y,ref double [] FY)

{FY[0] = Y[1] ; FY[1] = -Y[0] ;}}

Напишем программу, решающую задачу Коши двумя методами

static void Main(string[] args)

{double h = 0.1;double[] Y0 = {0, 1.0};

SystEuler Euler = new SystEuler(); Euler.Setlnit(0, Y0) ;

SystRK RK = new SystRK(); RK.Setlnit(0, Y0);

double t, REuler, RRK, Sin;

while (Euler.T < (2 * Math.PI + h / 2.0)) {

t = Euler.T; REuler = Euler.Y[0]; RRK = RK.Y[0]; Sin = Math.Sin(t);

Console.WriteLine("{0} {1} {2} {3} {4} {5}", t, REuler, RRK, Sin, Math.Abs(Sin - REuler), Math.Abs(Sin - RRK));Euler.NextStep(h); RK.NextStep(h);}Console.ReadKey(); }

Пример вывода графика

Форма с кнопкой

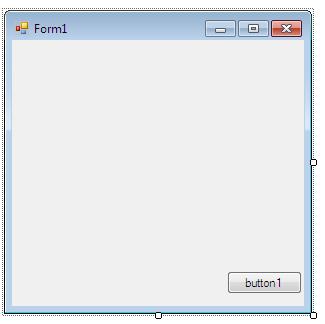
Код события нажатия кнопки:

string Text = "Graph0";

Size ClientSize = new Size(320, 230);

Chart myChart = new Chart();

myChart.Parent = this;

myChart.Left = 10;

myChart.Top = 10;

myChart.Width = (ClientSize.Width - 20);

myChart.Height = (ClientSize.Height - 20);

// Область в которой будет построен график

// (Их может быть несколько)

ChartArea myChartArea = new ChartArea();

myChartArea.Name = "myChartArea";

myChart.ChartAreas.Add(myChartArea);

// График (Их может быть несколько)

Series mySeries1 = new Series();

mySeries1.ChartType = SeriesChartType.Spline;

mySeries1.ChartArea = "myChartArea";

myChart.Series.Add(mySeries1);

// Исходные данные для графика

double[] yval1 = { 5, 6, 4, 6, 3 };

string[] xval = { "Январь", "Февраль", "Март", "Апрель", "Май" };

mySeries1.Points.DataBindXY(xval, yval1); }

Результат вывода графика: