Метод сложения/вычитания

Линейные уравнения

Линейное уравнение – уравнение, в котором полная степень любого многочлена равна 1. Это надо понимать так:

1) переменная не может быть ни в какой степени кроме 1,

2) переменная не может быть умножена на что-либо кроме числа.

Примеры линейных уравнений:

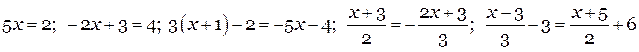
Разберем решение некоторых уравнений:

1) 5x = 2

Наше уравнение уже максимально упрощено, остается только «вылечить» Х от ненужной ему «5». Для этого поделим левую и правую части уравнения на 5.

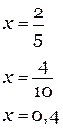
Ответ: {0,4}.

В решении этого уравнения мы воспользовались правилом:

Каждую часть уравнения можно умножать или делить на любое число кроме нуля.

2) -2x +3 = 4

Это уравнение надо упростить к виду предыдущего, т.е. все слагаемые с неизвестной собрать в левой части, а все числа собрать в правой.

-2x = 4 – 3

-2x = 1

Далее поступаем как в предыдущем примере:

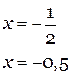
Ответ: {-0,5}.

В решении этого уравнения мы воспользовались правилом:

Любой многочлен уравнения можно переносить из одной части уравнения в другую, если поменять его знак на противоположный.

В нашем случае мы переносили (+3) из левой части в правую, где она стала уже (-3).

3) 3(x+1) – 2 = -5x – 4

Это уравнение тоже нужно сначала упростить. Для этого мы раскроем скобки и потом перенесениями соберем всё с Х в левой части, а без Х – в правой.

3x + 3 – 2 = -5x – 4

3x + 5x = -4 -3 + 2

8x = -5

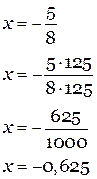
Ответ: {-0,625}.

4)

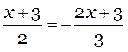
Это уравнение, на первый взгляд, не кажется линейным из-за наличия в нем дробей. На самом деле, его очень легко сделать линейным с помощью правила из пункта 1). Нужно домножить обе части уравнения на число, которое называется наименьшим общим кратным наших знаменателей (НОК знаменателей). Это такое число, которое делится на них нацело, т.е. оптимальное – число 6.

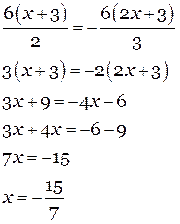
Ответ: { }.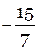

5) Последнее уравнение я запишу без текстовых комментариев. Постарайтесь в нем разобраться сами.

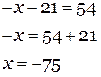
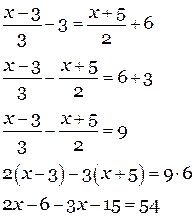
Системы линейных уравнений

Системой линейных уравнений – несколько линейных уравнений с несколькими переменными, объединенные знаком системы (фигурная скобка).

В школе мы обычно рассматриваем системы, в которых количество уравнений и переменных совпадают. Такие системы мы хорошо умеем решать. Рассмотрим методы решения систем линейных уравнений.

Методы решения систем

Мы знаем два метода:

1) Метод подстановки

2) Метод сложения/вычитания

В основе каждого метода лежит простая идея: сделать так, чтобы в каком-нибудь одном уравнении была всего одна неизвестная и найти её значение. После этого легко найти оставшиеся неизвестные.

Метод подстановки.

Когда мы пользуемся методом подстановки, мы из любого уравнения (наиболее удобного и простого) пытаемся выразить одну из переменных через другие переменные и числа. Как только у нас это получается, мы везде во всех других уравнениях подставляем вместо выраженной переменной её «заменитель», который мы выразили. Покажу это на примере.

Решить систему уравнений:

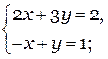
Оценим, из какого уравнения удобнее всего выражать переменную. Наиболее легким уравнением оказывается второе. Выразим из него переменную Y. Для этого перенесем (-х) в левую часть, поменяв знак перед ним. Так как порядок записи уравнений в системе не играет роли, то запишем это первой строкой, а второй строкой первое уравнение.

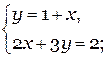
Подставим во второе уравнение вместо Y, равное ему выражение (1+х), так мы получим одну неизвестную в одном уравнении. А это мы уже умеем решать.

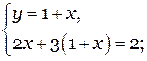
Раскроем скобки и произведем необходимые упрощения.

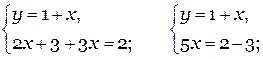
Теперь снова поменяем их местами, второе поставим на первую строчку, потом будем доупрощать и, наконец, подставим результат найденного Х в оставшееся уравнение, чтобы найти Y.

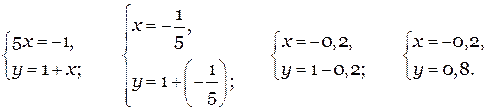
Решением системы двух уравнений с двумя неизвестными является пара чисел, которая записывается в круглых скобках через «;». Первым пишут Х, а вторым – Y.

Ответ: (-0,2; 0,8).

Метод сложения/вычитания.

Когда мы пользуемся методом сложения/вычитания, мы стремимся выровнять коэффициенты при одной из переменных, чтобы затем сложить или вычесть уравнения друг из друга. Тогда из-за равенства коэффициентов одна из переменных уничтожается, и мы получаем одно уравнение с одной неизвестной. Посмотрим на примере того же уравнения.

Решить систему уравнений:

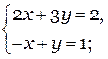
Уравнения в системе сейчас очень удобно записаны: каждые переменные с их коэффициентами записаны одни под другими. Это позволяет удобно и легко сравнивать коэффициенты при переменных. Следует всегда стремиться к такой записи.

Заметим, что при Х коэффициенты 2 и (-1), а при Y - 3 и 1. Будем выравнивать коэффициенты при Х. Для этого домножим левую и правую часть второго уравнения на 2.

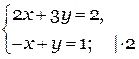
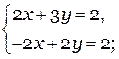
Теперь явно видно, что коэффициенты при Х в обоих уравнениях равны по модулю, т.е. только по самому числу, не считая знак. Если мы сложим друг с другом эти уравнения, то получим уравнение с одной переменной (Х исключится).

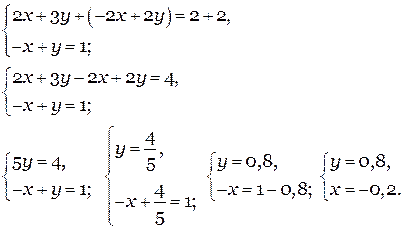
Ответ: (-0,2; 0,8).