Итерационное уточнение корней

Тема 1.2. Методы решения нелинейных уравнений

Постановка задачи

Отделение корней

1.2.2.1. Графическое отделение корней

1.2.2.2. Аналитическое отделение корней

Уточнение корней

1.2.3.1. Метод половинного деления

1.2.3.2. Метод итерации

1.2.3.3. Метод Ньютона (метод касательных)

1.2.3.4. Метод хорд

1.2.3.5. Сравнение методов решения нелинейных уравнений

Тестовые задания по теме «Методы решения нелинейных уравнений»

Постановка задачи

Одной из важнейших и наиболее распространенных задач математического анализа является задача определения корней уравнения с одним неизвестным, которое в общем виде можно представить как f(x) = 0. В зависимости от вида функции f(x)различают алгебраические и трансцендентные уравнения. Алгебраическими уравненияминазываются уравнения, в которых значение функции f(x)представляет собой полином n-й степени:

f(x) = Р(х) = a_n xⁿ + a₂ x² + …+ a₁ x + a₀ = 0.(1.2.1-1)

Всякое неалгебраическое уравнение называется трансцендентным уравнением. Функция f(x) в таких уравнениях представляет собой хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.

Решением уравнения f(x)=0называется совокупность корней, то есть такие значения независимой переменной 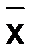, при которых уравнение обращается в тождество 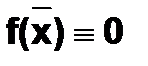. Однако, точные значения корней могут быть найдены аналитически только для некоторых типов уравнений. В частности, формулы, выражающие решение алгебраического уравнения, могут быть получены лишь для уравнений не выше четвертой степени. Еще меньше возможностей при получении точного решения трансцендентных уравнений. Следует отметить, что задача нахождения точных значений корней не всегда корректна. Так, если коэффициенты уравнения являются приближенными числами, точность вычисленных значений корней заведомо не может превышать точности исходных данных. Эти обстоятельства заставляют рассматривать возможность отыскания корней уравнения с ограниченной точностью (приближенных корней).

Задача нахождения корня уравнения с заданной точностью 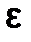( 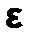>0)считается решенной, если вычислено приближенное значение 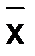, которое отличается от точного значения корня 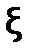не более чем на значение e

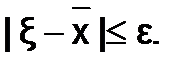(1.2.1-2)

Процесс нахождения приближенного корня уравнения состоит из двух этапов:

1) отделение корней (локализация корней);

итерационное уточнение корней.

На этапе отделения корней решается задача отыскания возможно более узких отрезков 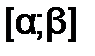, в которых содержится один и только один корень уравнения.

Этап уточнения корня имеет своей целью вычисление приближенного значения корня с заданной точностью. При этом применяются итерационные методы вычисления последовательных приближений к корню: x₀, x₁, ..., x_n, …, в которых каждое последующее приближение x_n+1вычисляется на основании предыдущего x_n. Каждый шаг называется итерацией. Если последовательность x₀, x₁, ..., x_n, …при n ® ¥ имеет предел, равный значению корня 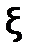, то говорят, что итерационный процесс сходится.

Существуют различные способы отделения и уточнения корней, которые мы рассмотрим ниже.

Отделение корней

Корень 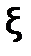уравнения f(x)=0считается отделенным (локализованным) на отрезке 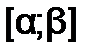, если на этом отрезке данное уравнение не имеет других корней. Чтобы отделить корни уравнения, необходимо разбить область допустимых значений функции f(x) на достаточно узкие отрезки, в каждом их которых содержится только один корень. Существуют графический и аналитический способы отделения корней.