Понятие линии (кривой) в школьном курсе математики

Первоначальные сведения о кривых дают наблюдения, связанные с натянутой нитью и дальнейшим её «искривлением».

Строгое определение линии (кривой), в широком понимании, дается в курсе «Дифференциальной геометрии и топологии», изучаемого студентами-математиками классических и педагогических специальностей университетов и педагогических ВУЗов.

Понятно, что в школьном курсе математики, а также в некоторых курсах анализа (высшей математики) ВУЗов, понятия линии и поверхности приходится рассматривать нестрого, т.е. интуитивно подразумевают под линией (кривой) фигуры, типа прямой, окружности, параболы синусоиды и т.д.

В физике рассматривается движение материальной точки в той или иной системе координат (ПДСК, полярной и т.д.) в зависимости от особенностей решаемых задач. При этом в выбранной системе отсчета устанавливается положение движущейся точки (на плоскости или в пространстве) для каждого момента времени.

Говорят, что множество точек (плоскости, пространства), через которые прошла материальная точка, образует линию, которую называют траекторией движения [1].

Данный вопрос тесно связан с методикой изучения метода координат. ([9], стр. 134).

Условиями, определяющими линию γв данной ПДСК на плоскости, являются уравнения, неравенства или их системы, но, как правило, рассматривают уравнение линии

.

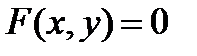(13)

Линия называется алгебраической, если в уравнении (13) 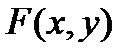- многочлен от переменных х и у, т.е. сумма членов вида

.

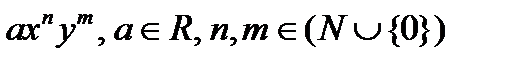Число 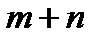(при 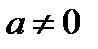) называется степенью одночлена.

Степенью многочлена 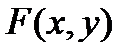называется наивысшая степень его членов.

Порядком алгебраической линии называют степень многочлена, определяемого уравнением (13).

Теорема. Понятие алгебраической линии, а также порядок линии не зависят от выбора ПДСК.

Примеры алгебраических линий в школьном курсе математики:

1. Линия первого порядка (прямая)

.

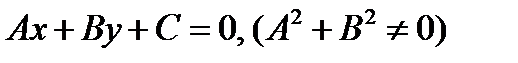2. Линия второго порядка:

a) Парабола ;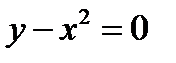

b) Окружность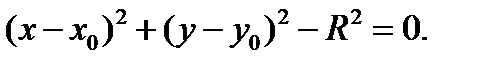

3. Линия n-го порядка:

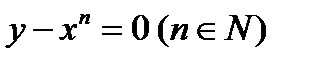
Замечание: Уравнение (13) рассматривают как уравнение линии, подразумевая при этом только то, что на плоскости существует линия γ, координаты (х,у) каждой точки которой удовлетворяют уравнению (13). При этом на плоскости могут существовать точки, координаты которых удовлетворяют уравнению (13), но они не составляют линию.

Пример:

1)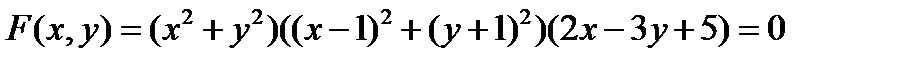

(14)

Фигура F, заданная уравнением (14) состоит из двух точек 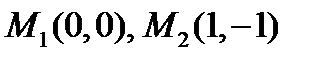, которые не составляют линию, и прямой .

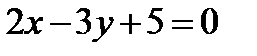2)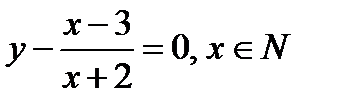

(15)

фигура, заданная уравнением (15), не является линией.

§2. Некоторые вопросы методики изучения линий на плоскости в школьном курсе математики.

В учебниках геометрии А.В. Погорелова; Л.С. Атанасяна и другие используется один и тот же вариант изложения метода координат на плоскости. Но роль координатного метода в этой учебной литературе не одинакова. Учебник Л.С. Атанасяна ограничивается незначительным использованием координат в изложении геометрии, в то время, в учебнике А.В. Погорелова для изучения геометрии используется координатный метод. Он широко использует его при доказательстве теорем, вводе определении и понятий. А.В. Погорелов в своем учебнике использует метод координат на плоскости по схеме: введение координат, координаты середины отрезка, расстояние между точками, уравнение окружности, уравнение прямой, координаты вектора. Атанасян излагает метод координат по другой схеме: координаты вектора, простейшие задачи в координатах, уравнения окружности и прямой.

Учащиеся уже знакомы с прямоугольной системой координат, поэтому введение этого понятия не вызывает трудностей. Основное внимание должно быть обращено на усвоение соответствующей терминологии и на формирование умения вычислять координаты заданной точки, строить точку по ее координатам, оптимально выбирать систему координат.

В перечисленных учебниках есть задачи на нахождение координат середины отрезка и расстояния между двумя точками.

С уравнениями некоторых фигур учащиеся знакомы из курса алгебры. Поэтому ознакомление с понятием уравнения фигуры осуществляется в процессе обобщения и систематизации знаний учащихся. В учебнике Погорелова [7] уравнением фигуры в декартовых координатах называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. И обратно, любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры. Для утверждения, что некоторое уравнение 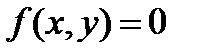является уравнением фигуры F, нужно доказать, что а) координаты любой точки фигуры F удовлетворяют уравнению 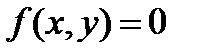, б) любые два числа, удовлетворяющие уравнению 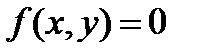, являются координатами некоторой точки фигуры F.

В учебнике Анатасяна [3] уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии. Для утверждения, что некоторое уравнение 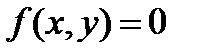является уравнением фигуры F, нужно доказать, что а) координаты любой точки фигуры F удовлетворяют уравнению 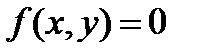; б) если точка М не принадлежит фигуре F, то ее координаты 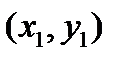не удовлетворяют уравнению 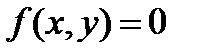, т.е. .

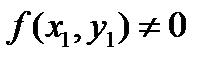Таким образом, в учебнике Погорелова логическая структура определения уравнения фигуры является конъюнкцией прямого и обратного утверждения, в учебнике Анатасяна – конъюнкцией прямого и противоположного ему утверждений. Логическая структура определения обусловливает характер пропедевтики. Так, в учебнике Погорелова при повторении и систематизации знаний, полученных в курсе алгебры, следует акцентировать внимание учащихся на том, что, например уравнение 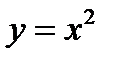является уравнением параболы, так как координаты любой точки параболы удовлетворяют уравнению 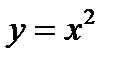и любые два числа, удовлетворяющие 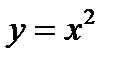, являются координатами некоторой точки параболы, не забывая обратить внимание учащихся на то, что координаты любой точки, не лежащей на данной кривой, не удовлетворяют данному уравнению.

В работе [9, гл. VII] рассмотрены вопросы, связанные с ролью координатного метода, его компонент, а в качестве примера приведена задача, при решении которой мы получаем кривую, приведенную в примере 2 параграфа 1 глава 2.

§3. Исследование функции 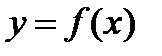и построение графиков в школьном курсе математики.