Тема 12 Основные теоремы и формулы теории вероятностей

Лекция 3.12.1 «Условные вероятности. Вероятности сложных событий»

Учебные вопросы:

1. Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей

2. Формула полной вероятности

3. Формула Байеса

Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей

Условные вероятности.

Аксиоматически определенную выше вероятность можно назвать безусловной вероятностью, подчеркивая этим, что она не зависит ни от каких дополнительных условий, кроме фиксированного комплекса условий 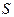, которым характеризуется опыт.

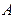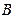Пусть в опыте, соответствующему некоторому комплексу условий, могут произойти случайные события и . Допустим также, что стало известно, что осуществилось событие 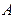. Эта новая информация равносильна дополнительному условию, накладываемому на опыт и адекватному осуществлению события 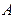. В изменившемся комплексе условий опыта изменится и вероятностное распределение на его поле событий.

Пусть 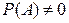. Условная вероятность 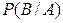наступления события 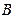при условии, что событие 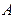произошло в результате данного опыта, определяется следующей аксиомой:

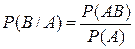. (4)

Условную вероятность 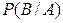для краткости называют «вероятность события 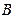при условии 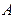». При 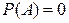условная вероятность 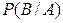не определена.

Пример. При бросании правильной игральной кости стало известно, что выпало четное число очков. Какова вероятность того, что выпала: а) двойка; б) пятерка?

◄ Исходное множество элементарных исходов для данного опыта 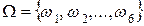, где 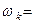{число выпавших очков равно 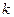}, содержит 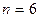исходов. Три из них благоприятствуют событию 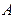={выпало четное число очков}, один исход благоприятствует событию 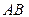, где 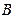={выпала двойка}. Число исходов, благоприятствующих событию 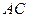, где 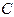={выпала пятерка}, равно нулю. По формуле (4) получаем: , . ►

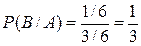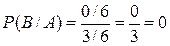На практике для вычисления условной вероятности 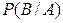часто применяется метод вспомогательного эксперимента, при котором формулируется новый опыт, соответствующий комплексу условий 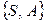. В этом новом комплексе условий получают соответствующее ему множество элементарных исходов 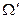. Безусловная вероятность осуществления события 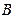в этом новом опыте и принимается за условную вероятность 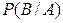. Этот метод обычно применяется в тех случаях, когда вероятностное пространство для вспомогательного опыта строится проще, чем для исходного.

Пример. В условиях предыдущего примера новым множеством исходов будет 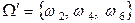. Один из этих исходов благоприятствует событию 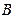={выпала двойка}, событию же 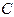={выпала пятерка} – ни один. По формуле классической вероятности получаем , .

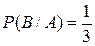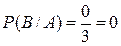Независимость событий

Понятие условной вероятности позволяет в свою очередь ввести в математической модели понятие независимости. Будем считать, что событие 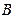не зависит от события 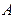, если выполняется равенство

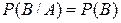. (5)

Если 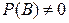, то из равенств (74) и (5) следует, что 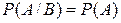, т. е. независимость является взаимным свойством: если 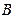не зависит от события 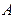, то и 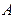не зависит от события 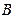. Более удобным определением независимости по сравнению с (5) является следующее.

События 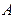и 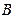называются независимыми, если

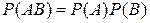. (6)

События 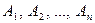называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для любого набора из 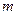событий ( 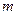=2, 3, …, 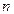) выполняется равенство

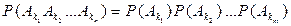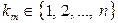, . (7)

Если (7) выполняется только при 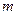=2, то события называютпопарнонезависимыми. Отметим, что из попарной независимости не следует независимость в совокупности.

Формулы (6) и (7) позволяют выделять независимые события в тех случаях, когда построена формализованная вероятностная модель случайного опыта и вероятности всех рассматриваемых событий определены. Однако далеко не всегда события, независимые в таком теоретико-вероятностном смысле, являются независимыми и в реальности. На практике в любых сомнительных случаях обычно стараются принять меры для объективной проверки гипотезы о независимости событий, основываясь на теоретико-вероятностной независимости, введенной равенствами (6) и (7), с причинной независимостью реальных событий. Решение подобных задач, основанное на применении методов проверки статистических гипотез, рассматривается в математической статистике.

Пример. В группе 25 студентов. Из них 10 человек курят, 13 носят очки, а 8 и курят и носят очки. Наудачу выбирается один студент. События: 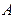={выбранный студент курит}, 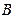={выбранный студент носит очки}. Установить, зависимы или нет события 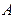и .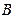

◄ Так как 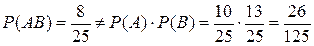, т. е. условие (6) независимости не выполняется, делаем вывод, что события 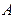и 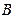зависимы.

Необходимо отметить, что полученный вывод справедлив лишь для данного частного эксперимента, и следует остерегаться распространять его на всех студентов вообще. Хотя гипотеза о зависимости между курением и состоянием зрения кажется разумной, для ее подтверждения необходимо было бы провести статистическое обследование всех студентов на определенной территории, которое включало бы проверку зрения у каждого и регистрацию длительности и интенсивности курения для тех, кто курит. Полученные статистические данные позволили бы на основе определенного критерия подтвердить либо отвергнуть наличие статистической зависимости между курением и состоянием зрения в той группе населения, которую составляют студенты. ►