Классификация краевых задач для ур. Гип. Типа

Классификация уравнений с частными производными 2-го порядка

2. Классификация уравнения 2-го порядка со многими независимыми переменными

Кононическая форма эллиптического, параболического и гиперболического уравнения

(в одном спрятано 3 вопроса, потому что идет одно доказательство ко всем, так в учебнике, не вижу смысла писать одно и тоже, просто на экзамене пишите про свое)

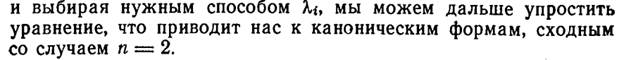
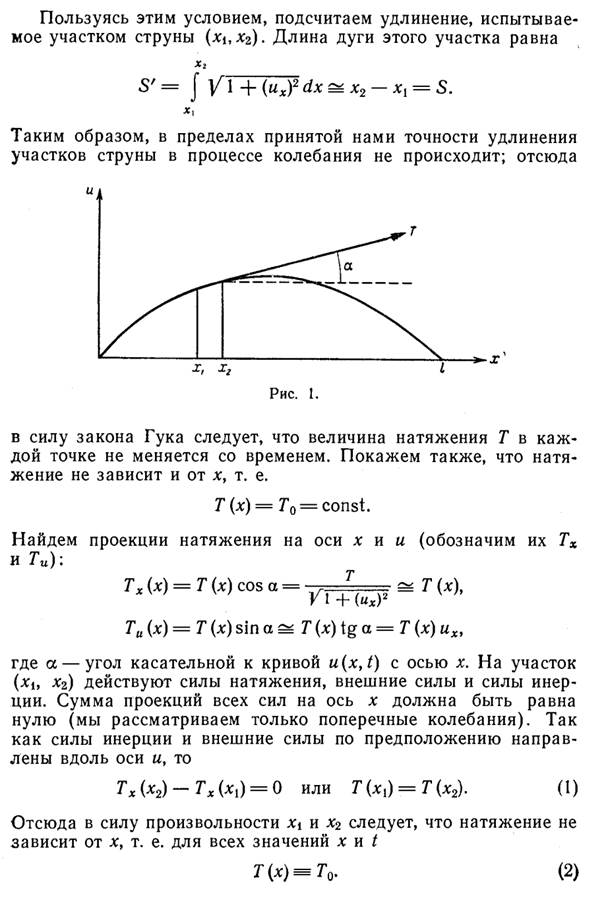
Уравнения поперечных колебаний струны

/

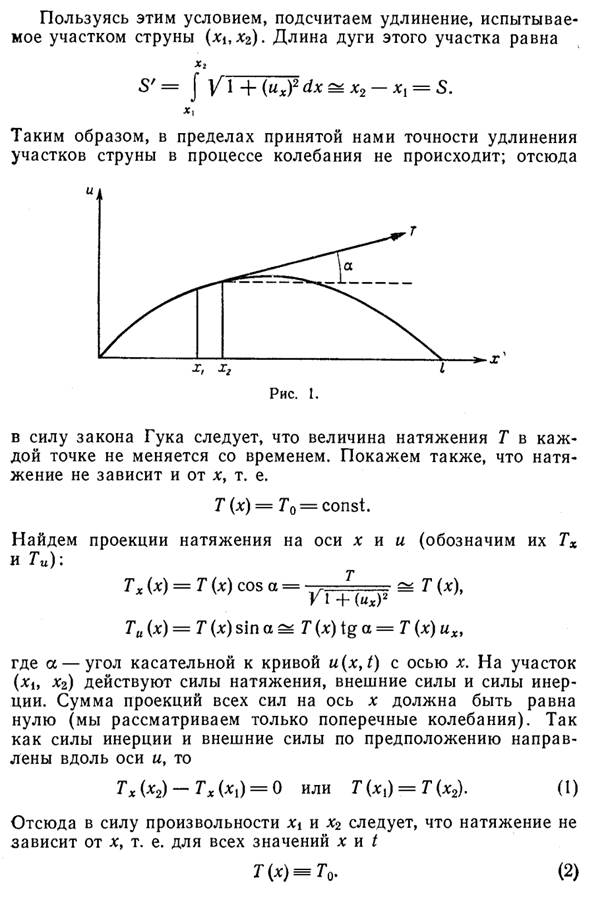
Уравнения продольных колебаний струны

Энергия колебаний струны

Поперечные колебания мембраны

Метод Даламбера, точка решения ур-ия гиперболического типа

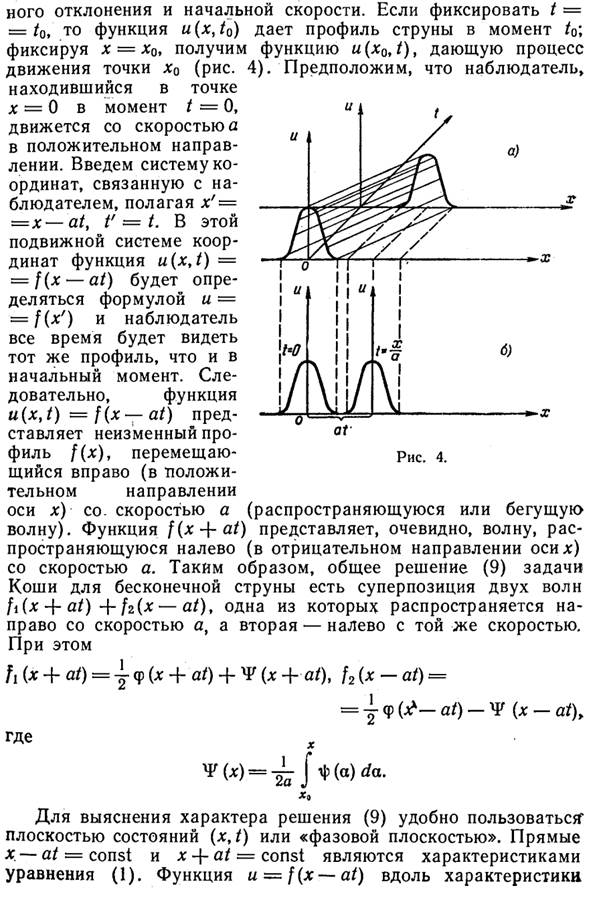
классификация краевых задач для ур. Гип. Типа

Когда в п.2.1 выводили уравнение колебаний струны, мы определили лишь то, что струна имеет длину l и функция u(x,t), определяющая отклонение от положения равновесия точки струны с абсциссой х в момент времени t, может удовлетворять начальным условиям. Однако мы ничего не сказали о состоянии концов струны, то есть, являются ли концы струны

1) жестко закрепленными;

2) свободными, т.е. могут свободно перемещаться по прямым, параллельным направлению отклонения u;

3) закрепленными упруго, т.е. каждый конец испытывает со стороны заделки сопротивление, пропорциональное отклонению и направленное противоположно ему;

4) двигающимися в поперечном направлении по заданным законам,

поскольку лишь такое знание позволяет корректно находить решение поставленных задач.

Задание состояния концов струны определяет краевые условия исходной задачи. Например,

1) Если концы струны жестко закреплены, то краевые условия имеют вид:

.

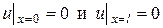2) В случае свободных концов для получения условия при х = 0 необходимо спроектировать на ось ординат Оu силы, действующие на некоторый участок струны. Так как натяжение в точке х = 0 действует лишь параллельно оси абсцисс Ох, то проекция сил натяжения на некоторый участок струны равна 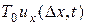. Проекция внешней силы равна 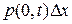, а проекция силы инерции равна - 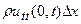. Приравнивая нулю сумму всех сил, получим

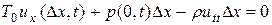. (48)

Устремив 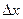к нулю, получим условие 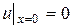. Аналогично можно получить условие на другом конце струны - .

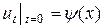3) Действие упругих сил заделки на левом конце дается выражением 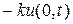, где k – коэффициент упругости упругого закрепления концов струны. В этом случае приравниваем нулю проекцию на ось и всех сил, действующих на некоторый участок, левый конец которого закреплен упруго. Тогда к левой части уравнения (48) добавится член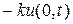

,

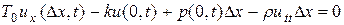а при 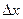→ 0, получим

.

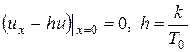На правом, упруго закрепленном конце (x = l), проекция всех сил имеет вид

,

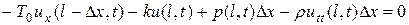поскольку

.

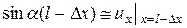При 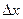→ 0, получим .

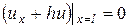4) Для этого случая краевые условия имеют вид

,

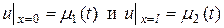где функции 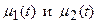определяют закон движения концов струны ( ).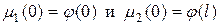