Методы решения систем линейных уравнений
Существуют три основных метода решений систем линейных уравнений.
1 Метод Крамера (Габриель Крамер (1704-1752) швейцарский математик)
Теорема Если в системе n линейных уравнений с n неизвестными определитель матрицы системы 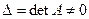 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
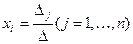 (1)
(1)
где 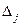 - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Формулы (1) называют формулами Крамера.
- определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Формулы (1) называют формулами Крамера.
Пример 5 Решить систему уравнений методом Крамера
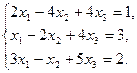
Решение: Найдем определитель системы:
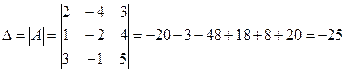 .
.
Т. к. 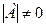 , то по теореме Крамера система имеет единственное решение. Вычислим определители матриц ∆1, ∆2, ∆3, полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов.
, то по теореме Крамера система имеет единственное решение. Вычислим определители матриц ∆1, ∆2, ∆3, полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов.
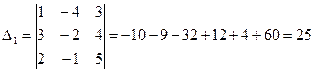 ;
;
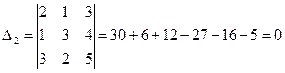 ;
;
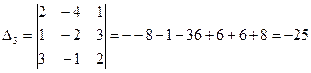 .
.
Теперь по формулам Крамера 
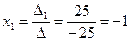 ;
; 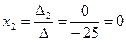 ;
; 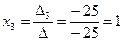 ,
,
т. е. решение системы (-1; 0; 1).
2 Метод обратной матрицы
Если система n линейных уравнений с n неизвестными записана в матричной форме АХ=В и 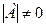 , то её решение находится методом обратной матрицы по формуле:
, то её решение находится методом обратной матрицы по формуле:
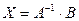 .
.
Пример 6 Решить систему методом обратной матрицы:
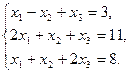
Решение: Запишем систему уравнений в матричной форме.
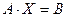 .
.
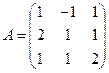 ,
, 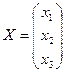 ,
, 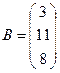 .
.
Решение матричного уравнения имеет вид
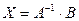 .
.
Найдем обратную матрицу А-1.
Для этого вычислим определитель матрицы А:
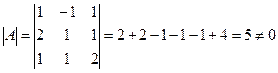 - следовательно матрица А имеет
- следовательно матрица А имеет
обратную матрицу А-1.
Найдем алгебраические дополнения матрицы А.
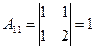 ;
; 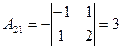 ;
; 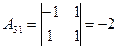 ;
;
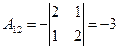 ;
; 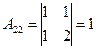 ;
; 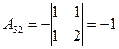 ;
;
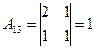 ;
; 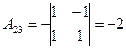 ;
; 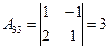 .
.
Таким образом,
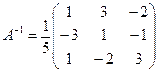 ,
,
откуда
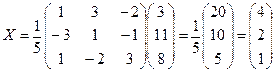 .
.
Следовательно, х1 = 4, х2 = 2, х3 = 1.
3 Метод Гаусса
Методом Гаусса можно решить любую систему уравнений общего вида. Для этого составляют расширенную матрицу системы (А/В), приписывая к матрице А столбец свободных членов В, и с помощью элементарных преобразований приводят матрицу к ступенчатому виду. По полученной матрице выписывают новую систему и решают ее методом исключения неизвестных: начиная с последних переменных, находят все остальные.
Пример 7 Решить систему методом Гаусса:
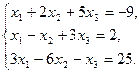
Решение: Подвергнем преобразованию расширенную матрицу данной системы. Вычтем из элементов второй строки соответствующие элементы первой строки, а из элементов третьей строки соответствующие элементы первой строки, умноженные на 3, получим
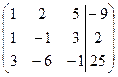 ~
~ 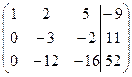 ~
~ 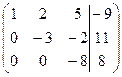 .
.
Используя полученную матрицу, выписываем преобразованную систему.
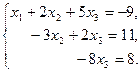
Система уравнений приняла треугольный вид.
Из последнего уравнения имеем х3= -1; подставляя это значение во второе уравнение, получаем х2 = -3 и, наконец, из первого уравнения находим х1 = 2.
Итак, решение системы (2; -3; -1).
РАЗДЕЛ 2 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Тема 2.1 Основы алгебры векторов
План:
1 Определение вектора
2 Действия над векторами
3 Линейная зависимость системы векторов
4 Базис. Координаты вектора
5 Координатные системы в трехмерном пространстве
6 Скалярное произведение векторов
7 Векторное произведение векторов
8 Смешанное произведение векторов
1 Определение вектора
Значение многих геометрических и физических величин полностью определяется заданием некоторого числа. Например, длина отрезка, масса тела, температура и т.д. Подобные величины называются скалярными. Поэтому числа иногда называют скалярами. Т.е., скаляр – это число. Другие геометрические и физические величины определяются заданием направления и числа. Примером может служить сила, приложенная к некоторой точке, т.к. важно знать в каком направлении она действует. Еще более простым примером является направленный отрезок прямой линии. Такие величины называют векторными, а простейшая из них – вектором.
Вектором называется направленный отрезок прямой, у которого различают начало и конец.
 В
В
А
Другими словами, вектор – это всякая упорядоченная пара несовпадающих точек (А, В), определяющая направленный отрезок с началом в точке А и концом в точке В.
Обозначение: 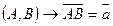 .
.
Длиной (модулем) вектора 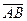 называется расстояние от точки А до точки В. Длина обозначается символами
называется расстояние от точки А до точки В. Длина обозначается символами 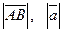 .
.
Направлением вектора 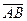 называется направление, определяемое лучом
называется направление, определяемое лучом 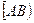 .
.
Вектор, задаваемый парой точек 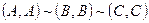 , называется нулевым вектором и обозначается
, называется нулевым вектором и обозначается 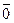 . Длина нулевого вектора равна нулю, а направление неопределено.
. Длина нулевого вектора равна нулю, а направление неопределено.
Вектор, длина которого равна единице, называется единичным вектором или ортом. Обозначают 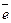 .
.
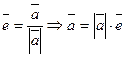 - стандартная формула вектора.
- стандартная формула вектора.
Два вектора называются равными, если их длины равны, а направления одинаковы.
Из этого определения вытекает, что:
1) начало вектора может быть перенесено в любую точку пространства. Поэтому вектор называют свободным;
2) два вектора, лежащих на параллельных прямых, можно перенести на одну прямую;








3) любые два вектора можно перенести на одну плоскость;







 a
a

Два вектора называются коллинеарными, если лежат в одной плоскости на параллельных прямых или на одной прямой. Они могут быть одинаково или противоположно направлены.
Для того чтобы два ненулевых вектора 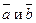 были коллинеарны, необходимо и достаточно, чтобы существовало число
были коллинеарны, необходимо и достаточно, чтобы существовало число 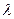 , удовлетворяющее
, удовлетворяющее
условию 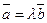 .
.
Векторы называются компланарными, если они лежат в одной плоскости (или их направления параллельны одной плоскости).
Действия над векторами
Сложение векторов
Пусть даны два вектора  и
и  . Возьмем произвольную точку А и отложим от нее вектор
. Возьмем произвольную точку А и отложим от нее вектор  . Получим точку В, от которой отложим вектор
. Получим точку В, от которой отложим вектор  .
.
         В А С В1 А1 С1 В А С В1 А1 С1 | 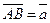 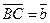 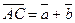 Суммой векторов Суммой векторов  и и  называют вектор, который идет из начала вектора к концу вектора называют вектор, который идет из начала вектора к концу вектора  , если , если  приложен к приложен к  . . |
Данное правило сложения векторов, называется правилом треугольника.
Убедимся, что введенное определение суммы двух векторов корректно, т.е. результат не зависит от выбора точки А.
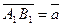
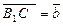
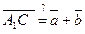
Рассмотрим четырехугольник АА1В1В. Он является параллелограммом, т.к. 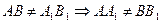 .
.
Четырехугольник ВВ1С1С - параллелограммом, т.к. 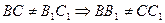 .
.
Так как 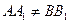 и
и 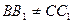 , то
, то 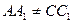 . Следовательно, четырехугольник АА1С1С также параллелограмм. Отсюда
. Следовательно, четырехугольник АА1С1С также параллелограмм. Отсюда 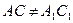 , т.е.
, т.е. 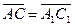 .
.
Свойства сложения векторов
10 Сложение векторов коммутативно
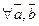
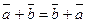
Доказательство: Построим сумму векторов  и
и  по описанному правилу треугольников. По определению отложим от т. А вектор
по описанному правилу треугольников. По определению отложим от т. А вектор 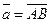 , от т. В вектор
, от т. В вектор 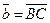 . Получим
. Получим 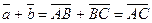 .
.
Дополним  до параллелограмма ABCD так, чтобы сторона AС была диагональю этого параллелограмма. Но у параллелограмма противолежащие стороны параллельны и равны.
до параллелограмма ABCD так, чтобы сторона AС была диагональю этого параллелограмма. Но у параллелограмма противолежащие стороны параллельны и равны.
B   A A 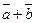 С С  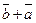       D D | Тогда 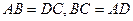 , , 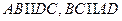 . Следовательно, . Следовательно, 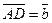 , , 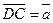 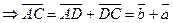 . Отсюда . Отсюда 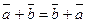 . . |
Замечание: Из полученного результата следует правило параллелограммасложения двух векторов:
Если векторы  и
и  приложены к общему началу, то их сумма есть вектор, совпадающий с диагональю параллелограмма, построенного на векторах
приложены к общему началу, то их сумма есть вектор, совпадающий с диагональю параллелограмма, построенного на векторах  и
и  , и идущий из их общего начала.
, и идущий из их общего начала.
20 Сложение векторов ассоциативно
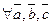
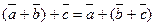
Правило многоугольника для сложения векторов.
В 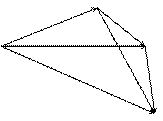   А А 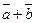 С С 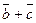 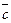 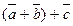 D D | Это равенство позволяет каждую сумму записывать без скобок 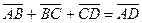 . . |
30 Поглощение нуль - вектора
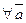
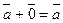
 В
В 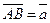
А 
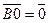
40 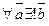 , имеющий с
, имеющий с  равную длину и противоположное направление. Его называют противоположным и обозначают
равную длину и противоположное направление. Его называют противоположным и обозначают 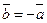 . Причем
. Причем 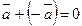 .
.

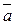 В
В 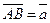 . Тогда
. Тогда 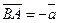
А 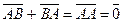
Вычитание векторов
Вычитание векторов вводится как операция, обратная сложению.
Пусть даны два вектора  и
и  . Разностью двух векторов
. Разностью двух векторов  и
и  называется такой вектор
называется такой вектор 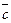 , который в сумме с вектором
, который в сумме с вектором  дает
дает  :
:
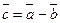 , если в сумме
, если в сумме 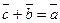 .
.
 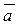 В В 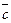 А А  С С | Возьмем произвольную точку А и отложим от нее вектора  и и  . . 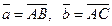 |
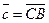 - искомый вектор, так как по правилу треугольника, чтобы получить вектор
- искомый вектор, так как по правилу треугольника, чтобы получить вектор  нужно к вектору
нужно к вектору  прибавить вектор
прибавить вектор 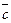 .
.
Из полученного чертежа следует способ построения разности двух векторов: если векторы  и
и  привести к общему началу, то
привести к общему началу, то 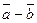 есть вектор, идущий из конца вычитаемого
есть вектор, идущий из конца вычитаемого  в конце уменьшаемого
в конце уменьшаемого  . Иными словами, разностью двух векторов является вектор, определяющий вторую диагональ параллелограмма, построенного на заданных векторах.
. Иными словами, разностью двух векторов является вектор, определяющий вторую диагональ параллелограмма, построенного на заданных векторах.
