Односторонние производные. Класс дифференцируемых производных. Теорема о связи непрерывности и дифференцируемости функции.
Если существует конечный предел, когда приращение аргумента рассматривается с правой стороны ( 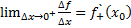 ) то этот предел называется правой производной
) то этот предел называется правой производной
Если существует конечный предел, когда приращение аргумента рассматривается с левой стороны ( 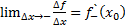 ) то этот предел называется левой производной
) то этот предел называется левой производной
Функция, имеющая производную в точке, называется дифференцируемой в этой точке.
Функция, имеющая правую(левую) производную в точке называется дифференцируемой справа(слева)
Функция, дифференцируемая в любой точке промежутка (а; b) называется дифференцируемой на этом промежутке.
Функция называется дифференцируемой на замкнутом промежутке [a;b] , если она дифференцируема на открытом промежутке (а;b), а так же слева в точке b и справа в точке а. Множество дифференцируемых функций в точке х0 образует класс дифференцируемых функций в этой точке.
Теорема о связи непрерывности и дифференцируемости функции:
Если функция дифф-ма на заданном промежутке, то она является непрерывной на этом промежутке.
f(x) принадл. D`(a;b) = f(x) принадл. C(a;b)
Вопрос №?
Приложения производных: эластичность функции, правило Лопиталя.
Эластичность функции:
Ex(y) = 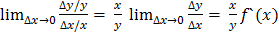
Частные случаи:
· |Ex(y)| <1 – не эластичная функция
· |Ex(y)| =1 – существует нейтральная эластичность (при умножении аргумента на 1% значение функции изменяется на 1%)
· |Ex(y)| >1 – эластичная функция
Вопрос №?
Теорема Ферма (с доказательством)
Теорема:Если дифференцируемая на промежутке Х функция y = f(x) достигает своего наименьшего или наибольшего значения в точке х0, то производная функция этой точки = 0.
|
 y
y
 |
f(x0+Δx)
 | |||||
 | |||||
 | |||||
 Х
Х
0 Х0 х0+Δх
.
Механический и экономический смысл производной
Механический смысл:
Пусть некоторая точка движется вдоль прямой не обязательно с постоянной скоростью. Тогда пройденное расстояние измеряется по закону S = S(t)
Необходимо вычислить скорость в момент времени t0
V(t0) - ?
Vср = 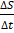
Естественно полагать, что предельной формой Vср при Δt→0 является скорость в момент времени t0
V(t0) = 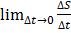 = S`(t0)
= S`(t0)
Механический смыслпроизводной – производная от закона S(t) = S
Экономический смысл:
Допустим, что объем произведенной продукции изменяется по закону U = U(t)
Необходимо вычислить производительность труда в момент Z(t0)
За время от
t0 до t0+Δt
произведено продукции от
U0 → U0 + ΔU
тогда
Zср = 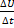
Z(t0) = 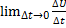 = U`(t0)
= U`(t0)
Вопрос №?

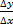 ≥ 0 (x>0) или
≥ 0 (x>0) или 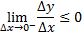
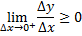 Т.к. функция дифференцируема на промежутке Х то значение производной не зависит от направления:
Т.к. функция дифференцируема на промежутке Х то значение производной не зависит от направления: 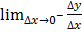 =
= 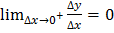 f`(x0) = 0
f`(x0) = 0