Сходимость метода итераций для решения системы алгебраических уравнений
Теорема: Система уравнений имеет единственное решение и сходится при любом начальном значении 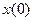 тогда и только тогда, когда все собственные значения матрицы
тогда и только тогда, когда все собственные значения матрицы 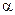 по модулю меньше 1.
по модулю меньше 1.
Если для системы уравнений
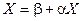
выполнено хотя бы одно из условий:
1. 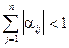 ,
, 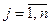
2. 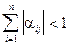 ,
, 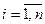
то процесс итерации сходится, независимо от выбора начального условия.
Однако этой теоремой в общем случае очень тяжело воспользоваться, поэтому на практике пользуются другим правилом менее жёстким.
Если эти условия выполняются, то в принципе логично выбрать для начальных значений. На практике в качестве начального приближения используют вектор свободных членов.
Приведение линейной системы к виду, удобному для итерациию.
Теорема сходимости накладывает жёсткие условия к коэффициентам данной линейной системы.
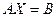
Однако, если 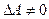 , то эту систему всегда можно привести к такому виду:
, то эту систему всегда можно привести к такому виду:
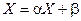 , чтобы удовлетворить условиям 1
, чтобы удовлетворить условиям 1
Первый способ.
Дано: 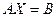
Домножим это уравнение на матрицу 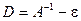 , где
, где 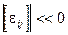
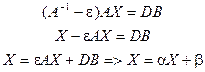 ,
,
где 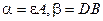
Второй способ.
Каждое 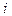 -ое уравнение делится на
-ое уравнение делится на 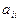
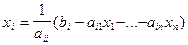
Тогда 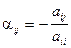 ,
, 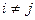 ,
, 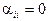 .
.
Тогда уравнение сходимости имеет вид
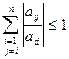 ,
, 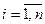
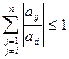 ,
, 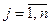
Эти неравенствабудут выполняться, если диагональные элементы будут удовлетворять условиям:
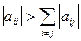 ,
, 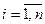 ,
,
то есть если модули диагональных коэффициентов для которого уравнения системы больше суммы модулей всех остальных коэффициентов.
Достоинства метода итераций
1. Если итерации сходятся быстро, то есть для сходимости требуется менее 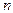 итераций, то выигрыш во времени по сравнению с методом Гаусса:
итераций, то выигрыш во времени по сравнению с методом Гаусса:
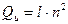 ,
, 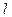 - число итераций
- число итераций
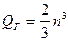
2. Погрешности округления в методе итераций сказывается значительно меньше, чем в методе Гаусса. Кроме того, метод итерации является самоисправляющимся, то есть отдельная ошибка запрещается в вычислениях, не отражаясь на конечном результате, то есть ошибочное приближение можно рассматривать как новый начальный вектор.
3. Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю.
4. Метод итераций легко программируется.
Метод Зейделя
Является модификацией метода итераций. Основная идея заключается в том, что при вычислении 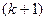 -го приближения
-го приближения 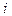 -го корня используются уже вычисленные
-го корня используются уже вычисленные 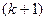 приближённые корни
приближённые корни 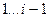 .
.
Дано: 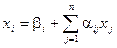 ,
, 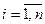
Выбираем начальное приближение:
На  -том шаге, согласно Зейделю строим приближение по следующим формулам:
-том шаге, согласно Зейделю строим приближение по следующим формулам:
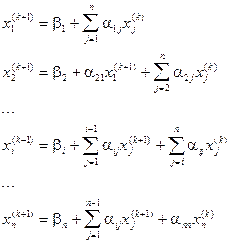
1. Метод Зейделя даёт полную сходимость по сравнению с методом итерации, но приводящий к громоздким вычислениям.
2. Теорема: Для существования единственного решения системы сходимости метода Зейделя достаточно выполнение хотя бы одного из двух условий:
1) 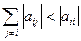 ,
, 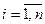
2) матрица 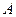 - симметричная положительно определённая (все её соответственно значения положительны)
- симметричная положительно определённая (все её соответственно значения положительны)
