Смешанное произведение векторов
Определение:Смешанным (векторно-скалярным) произведением векторов 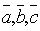 называется число, определяемое по формуле:
называется число, определяемое по формуле: 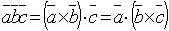 .
.
Свойства смешанного произведения:
1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. 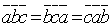 .
.
2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. 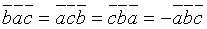 .
.
3.Необходимое и достаточное условие компланарности трех векторов 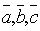 :
: 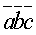 =0.
=0.
4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. 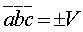 .
.
Если известны координаты векторов 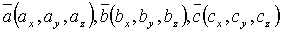 ,то смешанное произведение находится по формуле:
,то смешанное произведение находится по формуле: 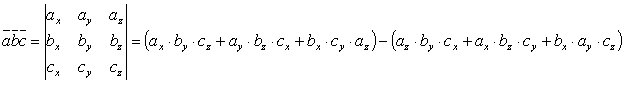
Пример:Вычислить смешанное произведение векторов 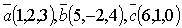 .
.
Решение: 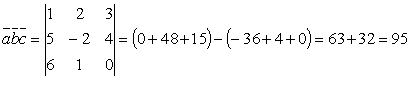
Способы задания прямой на плоскости. Взаимное расположение двух прямых. Угол между прямыми. Геометрический смысл знака выражения 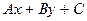 .
.


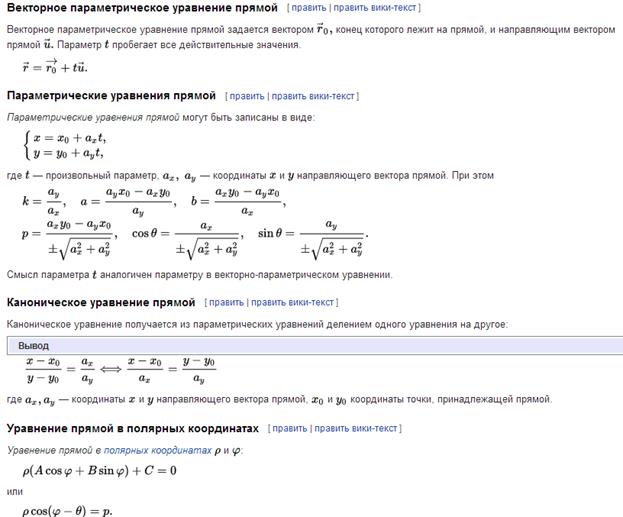

Теорема. Пусть
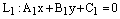 и
и 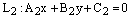
– общие уравнения двух прямых на координатной плоскости Оху. Тогда
1) если 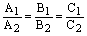 , то прямые
, то прямые 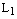 и
и 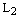 совпадают;
совпадают;
2) если 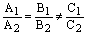 , то прямые
, то прямые 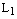 и
и 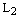
параллельные;
3) если 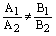 , то прямые пересекаются.
, то прямые пересекаются.
Доказательство. Условие 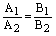 равносильно коллинеарности нормальных векторов данных прямых:
равносильно коллинеарности нормальных векторов данных прямых:
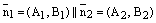 . Поэтому, если
. Поэтому, если 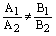 , то
, то 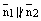 и прямыепересекаются.
и прямыепересекаются.
Если же 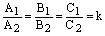 , то
, то 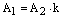 ,
, 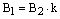 ,
, 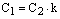 иуравнение прямой
иуравнение прямой 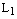 принимает вид:
принимает вид:
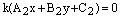 или
или 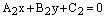 , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности
, т.е. прямые совпадают. Заметим, что коэффициент пропорциональности 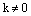 , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.
, иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.
Если же прямые не совпадают и не пересекаются, то остается случай 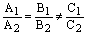 , т.е. прямые параллельны.
, т.е. прямые параллельны.
Теорема доказана.
Заметим, что если прямые пересекаются, то для нахождения координатих точки пересечения достаточно решить систему двух уравнений сдвумя неизвестными:
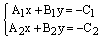 . (4)
. (4)
Следствие. Пусть 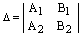 – определитель системы (4). Если
– определитель системы (4). Если 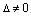 , то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:
, то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:
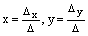 , (5)
, (5)
где 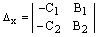 ,
, 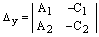 .
.
Если 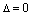 , то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.
, то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.
Доказательство. По определению определителя второго порядка
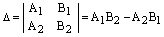 .
.
Если 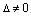 , то
, то 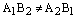 и
и 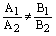 , т.е. прямые пересекаются икоординаты точки пересечения можно найти по формулам Крамера (5).
, т.е. прямые пересекаются икоординаты точки пересечения можно найти по формулам Крамера (5).
Если же 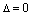 , то
, то 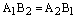 и
и 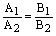 , т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.
, т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.
следствие доказано.
Пример. Выяснить взаимное расположение двух прямых
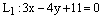 и
и 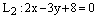
и если они пересекаются, найти их точку пересечения.
Решение. Решим систему
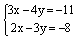 .
.
Определитель системы
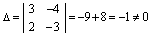 ,
,
следовательно прямые пересекаются. Вычисляем координаты точки пересечения:
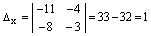 ,
, 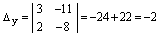 ,
,
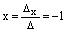 ,
, 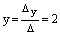 .
.
Ответ. Прямые пересекаются в точке 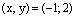 .
.
Пусть две прямые  и
и  заданы общими уравнениями
заданы общими уравнениями
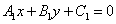 и
и 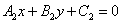 .
.
Так как нормальным вектором прямой 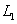 является вектор
является вектор 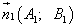 , а нормальным вектором прямой
, а нормальным вектором прямой 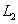 является вектор
является вектор 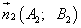 , то задача об определении угла между прямыми
, то задача об определении угла между прямыми 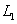 и
и 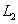 сводится к определению угла
сводится к определению угла 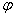 между векторами
между векторами 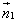 и
и 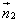 .
.
Из определения скалярного произведения 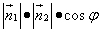 и из выражения в координатах длин векторов
и из выражения в координатах длин векторов 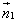 и
и 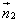 и их скалярного произведения получим
и их скалярного произведения получим
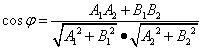 . (1)
. (1)
Итак, угол между прямыми, заданными общими уравнениями, определяется с помощью формулы (1).
Пример 1. Найти угол между прямыми, заданными общими уравнениями 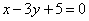 и
и 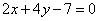 .
.
Решение. Используя формулу (1), получаем:
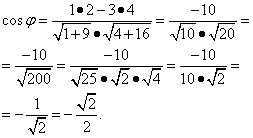
Получаем угол 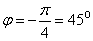 .
.
