Задания для контрольной работы

ОБЩИЕ ТРЕБОВАНИЯ

Учебным планом предусмотрено выполнение домашней контрольной работы по предмету «Основы гидростатики и гидродинамики». К выполнению домашней контрольной работы необходимо приступить только после полного изучения теоретического материала, согласно содержанию программы. Учебный материал рекомендуется конспектировать.

При изучении теоретического материала, решении задач следует пользоваться международной системой единиц СИ и применять обозначения единиц измерения согласно ГОСТ.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа выполняется по вариантам. Каждый вариант содержит два теоретических вопроса и пять задач. Студент, выполняет тот вариант, который соответствует последним двум цифрам его шифра, а данные выбирает по последней цифре шифра.

При выполнении контрольной работы должны быть выполнены следующие требования:

1. Контрольная работа выполняется после изучения всего теоретического материала

2. Ответы на теоретические вопросы и решение каждой задачи нужно начать с новой страницы

3. Если в данных для решения задач размерность не в единицах СИ, то в условии необходимо сделать их соответствующий пересчет

4. Отчет на теоретические вопросы рекомендуется выполнять кратко, полностью переписывая лишь точные формулировки и законы

5. Если к задаче прилагается схема или рисунок, их необходимо выполнять аккуратно карандашом с нанесением необходимых размеров и данных

6. В конце контрольной работы дается список использованной литературы

7. После списка литературы следует оставлять 1-2 страницы чистыми для написания рецензии.

8. Если студент выполняет не свой вариант, работа возвращается без проверки

Методические указания к решению задач

К задачам 1-2 Необходимо воспользоваться знанием физических свойств жидкостей:

а) коэффициентом температурного расширения

β_t = 1 * ∆V , 1 (1)

V₁ * ∆t ⁰С

где V- первичный объем жидкости;

∆V- изменение этого объема при повышении температуры на ∆t

б) коэффициентом объемного сжатия

β_V = - 1 * ∆V , 1

V₁ * ∆Р Па (2)

где V- первичный объем жидкости, м³

∆V- изменение этого объема при повышении давления на величину ∆Р

Знак «- » указывает на уменьшение объема при возрастании давления

К задачам 3-6 Необходимо руководствоваться тем условием, что жидкость находится в равновесии. Затем найдите нужную поверхность равных давлений – самую нижнюю границу раздела жидкостей, на которой давления во всех точках равны, как давления в точках одного и того же объема покоящейся жидкости. расположенные на одной горизонтали. Затем составьте уравнение равновесия:

Р = Р_О + ρgh (3)

где Р_О – давление в любой точке, Па

ρgh – величина избыточного давления, Па

К задачам 7-11 Данные задачи на определение силы гидростатического давления на боковые плоские стенки

F= Р_С S, н (4)

где Р_С = Р_О + ρgh_С - давление в центре тяжести смоченной боковой стенки,Па

h_С – глубина погружения центра тяжести под уровень жидкости, м

Сила F прикладывается в центре давления, положение которого определить

можно по формуле:

ℓ_Ц.Д = h_С + J_С

h_С S , м (5)

где h_С – глубина погружения центра тяжести стенки под уровень жидкости,м

J_С - момент инерции (справочный материал). Наиболее часто в практике встречаются следующие фигуры:

круг – J_С = πd⁴ / 64

прямоугольник – J_С = в Н³/ 12

в – ширина, м

Н – высота прямоугольника, м

S – площадь смоченной поверхности, м²

В задаче 7 для определения значения подъемной силы нужно использовать формулу:

Т = G + Ff (6)

где G – вес щита, кг

F – сила гидростатического давления, н

f - коэффициент трения

В решении задачи 10 равнодействующую сил давления определите как:

F = F₁ – F₂ (7)

где F₁ – сила гидростатического давления слева, н

F₂ – сила гидростатического давления справа, н

Для нахождения центра давления F необходимо составить уравнение моментов, учитывая, что момент равнодействующей равен сумме моментов составляющих.

В решении задачи 11 уравнение моментов всех сил составляется относительно точки О.

К задачам 12,13. Необходимо определить горизонтальную и вертикальную составляющие силы гидростатического давления на криволинейную поверхность.

Горизонтальная составляющая F_Г, определяется, как сила гидростатического давления на плоскую боковую стенку, которой является вертикальная проекция смоченной криволинейной поверхности ( в задачах это круг):

F_Г = Р_С S_ПР , Н (8)

где Р_С – давление в центре тяжести вертикальной проекции, смоченной поверхности, Н

S_ПР – ее площадь, м²

Вертикальная составляющая F_В определяется весом жидкости в объеме тела давления. Тело давления определяется путем построения. При этом нужно определить положение пьезометрической поверхности, воспользовавшись данными показаниями манометра Р_М:

h_П.П = Р_М

ρg , м (9)

где Р_М- манометрическое (избыточное ) давление, Па

отложив эту высоту вверх от точки подсоединения манометра.

В данном случае усилия, разрывающие резервуары по горизонтальным сечениям направлены вертикально ( на верхнюю половину – вверх, на нижнюю – вниз). Так как нижние половины резервуаров опираются на опоры, то усилие, направленное вниз уравновешивается реакцией опор.

Таким образом нужно определить вертикальную составляющую, направленную вверх.

К задачам 14,15 Используйте закон Архимеда и определите выталкивающую силу, определив объем погруженной части тела:

F_АРХ = ρgV_Т (10)

где ρ – плотность жидкости, кг/м³

V_Т – объем тела давления, м³

К задаче 16 При решении необходимо записать соотношение скоростных напоров для сечений 1и 2, воспользовавшись уравнением неразрывности потока υ₁s₁ = υ₂s₂, определите искомое через соотношение диаметров.

К задаче 17 Дважды составляется уравнение Бернулли для потока идеальной жидкости.

В начале для сечений, проведенных по свободной поверхности в резервуаре и на выходе из трубы с диаметром d₂.

Затем для сечений, проведенных через сечение в трубе с диаметром d₁, в месте подсоединения пьезометра и на выходе из трубопровода с диаметром d₂.

К задаче 18 Составьте уравнение Бернулли для потока реальной жидкости для данных сечений и определите потребный напор. Затем определите мощность на валу турбины.

N= ρg Н _ПОТРQ , Вт

Η (11)

где Q – расход жидкости в м³/с

Н_ПОТР – потребный напор, м

Н_ПОТР = Н_СТ + кQ^m , м (12)

где Н_СТ - статический напор, включающий геометрическую высоту ∆z, на которую необходимо поднять жидкость в процессе ее движения по трубопроводу и пьезометрическую высоту в конечном сечении трубопровода Р/ ρg, т. е.

Н_СТ = ∆z + Р₂/ ρg , м (13)

к, m – коэффициенты, зависящие от режима течения жидкости:

для ламинарного режима течения :

к = 128 νℓ , m = 1

πd⁴g (14)

где ℓ - фактическая расчетная длина трубопровода

для турбулентного режима течения:

к = ( λ_Т ℓ + ∑ζ ) ___8_

d π²d⁴ g , m = 2 (15)

К задаче 19 Решение заключается в определении:

а) общего уменьшения потерь напора во всасывающей линии

∆h_1-2 = ∆h_ТР + ∆h_М.П (16)

где ∆h_ТР = h_ТР1 – h_ТР2 – уменьшение потерь напора на трение, для

определения которых используется формула Дарси – Вейсбаха, м

∆h_М.П = h_М.П1 – h_М.П2 – уменьшение местных потерь напора, для

определения которых используется формула Вейсбаха, м

б) уменьшение затрат мощности

∆N = ρg∆h_1-2Q, Вт

Η (17)

где Q – расход жидкости, м³/с

Тогда годовая экономия электроэнергии

А = ∆NТ, Вт с; МВт ч (18)

где Т- количество секунд в году

К задаче 20 По падению давлении ∆Р₁ и ∆Р₂ определите потери напора на трение. Предположив, что жидкость двигается одна и та же и, задавшись вязкостью, определите режим движения, зону гидравлических сопротивлений и эквивалентную шероховатость ∆.

К задаче 21 Определите потери напора на трение при диаметре трубопровода d и после его уменьшения на 2δ, после чего определите их соотношение.

К задаче 22 Определите сумму потерь напора на трение при движении жидкости по НКТ и по кольцевому пространству в обсадной колонне, используя формулу Дарси – Вейсбаха. При определении потерь напора при движении жидкости по кольцевому пространству необходимо в формуле Дарси – Вейсбаха диаметр d заменить на гидравлический радиус R, учитывая, что d = 4R.

К задаче 23 Выразите через известные разности давление ∆Р₁ и ∆Р₂ местные потери напора, используя формулу Вейсбаха ξ υ² = h_М.П, откуда

2g

определите коэффициент местного сопротивления задвижки ξ.

К задаче 24 Составив уравнение Бернулли для потока реальной жидкости определите из него Р₂, то есть конечное избыточное давление в трубопроводе и сравните его с данным Р_К. Если полученное давление Р₂ ≥ Р_К, значит насос сможет обеспечить перекачку жидкости.

К задаче 25 Определив критический перепад давления, соответствующий смене режима, сравните его с данным перепадом.

К задаче 26 Для определения расхода Q воспользуйтесь формулой Дарси:

λ = 0,02 + 0,0005

d (19)

К задаче 27 Давление на выходе из трубопровода считайте атмосферным и примите за 10⁵ Па.

К задаче 28 Составьте уравнение Бернулли для потока реальной жидкости для сечения 1, проходящего по уровню жидкости в резервуаре и для сечения 2, проходящего по оси насоса и определите Р₂. Переведите при этом атмосферное давление из мм. рт.ст. в Па.

К задаче 29 Задачу решите графическим путем, построив график зависимости Н_ПОТР = f ( d ). Для этого необходимо задаться рядом значений диаметра d и по ним подсчитать Н_ПОТР, используя формулу (12):

Н_ПОТР = Н_СТ + kQ^m

где Q – расход жидкости м³/с

к, m – коэффициенты, зависящие от режима течения жидкости

Н_СТ - статический напор, определяемый по формуле (13):

Н_СТ = ∆Z + Р₂/ρg

к, m – коэффициенты, зависящие от режима течения жидкости, определяются по формулам (14, 15):

для ламинарного режима течения:

k= 128 νℓ m=1

πgd⁴

где ℓ - фактическая расчетная длина трубопровода

для турбулентного режима течения:

k =( λ ℓ + ∑ξ) _8__ m=2

d gπ²d⁴

Режимом необходимо задаться используя значение вязкости ν. При вязкости, равной десятым долям единицы и более – режим ламинарный.

Затем строят график Н_ПОТР = f (d) и по нему, зная Н_ПОТР определяют d

К задачам 30-32 Вначале определите скорость движения бензина с использованием уравнения неразрывности потока.

Q = υs (20)

где Q – расход бензина, м³/с

υ – скорость движения, м/с

s – площадь живого сечения; s = πd² , м²

Затем необходимо определить:

С – скорость распространения волны гидравлического удара

__

| К

С = √ ρ_______ , м/с

√ 1+ Кd / Еδ (21)

где К- модуль упругости жидкости, Па

d – внутренний диаметр трубы, мм

Е – модуль упругости материала трубы, (для стали Е ≈ 200 ГПа)

δ – толщина стенки трубы, мм

∆Р – ударное повышение давления( формула Жуковского), справедлива для прямого гидравлического удара, т.е. когда время закрытия задвижки

t_З < Т, Т– фаза удара:

∆Р = ρсυ (22)

где ρ – плотность жидкости, кг/м³

с – скорость распространения ударной волны, м/с

υ – кинематическая вязкость, м²/с

Если t_З > Т, удар называется непрямым и ударное повышение давления ∆Р определяется по формуле:

∆Р = ρсυ( Т/ t_З ) (23)

Т – фаза гидравлического удара, т.е. время пробега волны от задвижки до воздушного колпака и обратно:

Т = 2ℓ/с, с (24)

где ℓ - длина трубопровода от места его перекрытия до сечения, в котором давление считается постоянным, м

Определите скорость течения воды в трубе до закрытия задвижки, исходя из уравнения Бернулли:

Н = υ² + λ ℓυ²

2g d 2g (25)

где Н – напор воды в баке, м

ℓ, d- размеры трубопровода, м

λ – коэффициент гидравлического сопротивления

g – ускорение свободного падения, м/с²

Затем определяются скорости распространения волны гидравлического удара С, м/с и повышение давления ∆Р, Па в стальной трубе и в чугунной трубе – С₁, м/с и ∆Р₁, Па и сравниваются ∆Р и ∆Р₁.

К задачам 33- 35 Необходимо воспользоваться формулами для определения, необходимой для движения вязко – пластичных жидкостей, разности давлений ∆Р_О:

∆Р_О = 4τ_О ℓ , Па (26)

d

где τ_О – напряжение сдвига, Па

ℓ - длина трубопровода, м

d – диаметр трубопровода, м

и расхода нефти Q= πd²___ (∆Р – 4 ∆Р_О), м³/с

128 ηℓ 3 (27)

предполагая, что режим движения структурный -

т. е в начале движения неньютоновской жидкости весь поток жидкости движется целиком как твердое тело с одинаковой скоростью по всему поперечному сечению. По мере увеличения разности давлений возрастает и скорость движения жидкости, а радиус ее центральной части (ядро), где жидкость по-прежнему продолжает двигаться как твердое тело, постепенно уменьшается. Режим движения жидкости, характеризующийся наличием центрального ядра, называют структурным

где η – пластическая вязкость, Па*с

ℓ - длина трубопровода, м

d – диаметр трубопровода, м

После определения расхода нужно проверить режим течения, воспользовавшись формулой для определения обобщенного числа Рейнольдса:

Rе = _____1______

η + τ_{О___}

ρυd 6ρυ² (28)

где η – пластическая вязкость, Па*с

ρ – плотность, кг/м³

υ – кинематическая вязкость, м²/с

τ_О – напряжение сдвига, Па

В условиях задач, когда рассматривается плоско – радиальная фильтрация несжимаемой жидкости, дебит скважины определяется формулой Дюпюи:

Q = 2πkh * Р_К - Р_С

η ℓn R_К

r_С (29)

где R_К – радиус контура питания или влиянии скважины, м

Р_К - Р_С – разность давлений называется депрессией, Па

при определении дебита нагнетательных скважин, используемых при заводнении пластов, в числителе записывается разность давлений Р_С – Р_К – называемая репрессией, так как Р_С >Р_К

r_С –радиус скважины, м

k – коэффициент проницаемости, м²

h- толщина пласта, м

Под действием Р_К – (давление контура питания), уровень жидкости поднимается в скважине до статического. Пока скважина не эксплуатируется, в любой точке пласта давление Р_К и статический уровень Н_К можно определить по показанию манометра при открытой задвижке Р_М и глубине залегания пласта- Н_К = Р_К/ ρg = >

Р_К = Н_К ρg, Па (30)

Для того, чтобы жидкость притекала к скважине, необходимо снизить давление на ее забое (нижней точке) – Р_С, т. е создать условие Р_К > Р_С,

Р_С = Н_С ρg, Па (31)

где Р_С – давление на забое скважины определяется через динамический

уровень жидкости в скважине Н_С:

Н_С = Р_С / ρg (32)

Примеры решения задач

Пример 1

В Вертикальном цилиндрическом резервуаре диаметром d= 4м хранится 100т нефти с плотностью ρ_О =850 кг/м³ при н.у. β_t = 0.00072 1/ ⁰С. Определить изменение уровня нефти в резервуаре при изменении температуры на

∆t =30⁰С.

Решение:

1. Объем, занимаемый нефтью при t₁ = 0⁰

V = m/ρ₀ = 100 10³/850 = 118 м³

2. Изменение объема ∆V при изменении температуры на ∆t:

∆V = β_tVt = 0.00072 * 118* 30 = 2,55 м³

2. Изменение уровня нефти в резервуаре:

h = ∆V = 4∆V = 4*2,55 = 0,203 м

S πd² 3,14*16

Пример 2

Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двухжидкостного ртутного манометра.

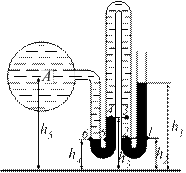h₁ = 82 см

h₂ =39 см

h₃ =54 см

h₄ = 41 см

h₅ = 100 см

ρ_В = 100 кг/м³

ρ_РТ = 13600 кг/м³

Решение:

Так как жидкость находится в равновесии, то давление в точке 1 и точке 2 равны как давления в точках одного и того же объема однородной жидкости, расположенных на одной горизонтали, то есть Р₁ = Р₂ на том же основании Р₃ = Р₄, а Р₅ =Р₆.

Тогда избыточное давление:

Р₁ = ρ_РТg (h₁ – h₂)

Р₃ = Р₂ – ρ_Вg (h₃ – h₂)

Р₅ = Р₄ + ρ_РТg ( h₃ – h₄)

Р_А = Р₆ – ρ_Вg (h₅ – h₄);

Исключив из этих соотношений промежуточные давления Р₂, Р₄, Р₆, получим:

Р_А = ρ_РТg [(h₁ – h₂) + (h₃ – h₄)] – ρ_Вg [( h₃ - h₂) + ( h₅ – h₄)] =

= 1.36*10⁴* 9,81(0,43 + 0,13) – 10³ *9,81(0,15+0,59) = 67,4 кПа.

Пример 3

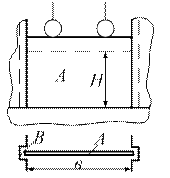Вертикальный щит А, перекрывающий водослив плотины, может перемещаться в пазах вверх и вниз.

Глубина жидкости Н = 1,4 м. Ширина щита

В_В = 2,6 м.

Какую силу нужно приложить, чтобы поднять щит, если вес его G = 32 кН, а коэффициент трения щита о пазы f = 0,3.

Решение:

1. Определим силу гидростатического давления на щит, так как атмосферное давление действует на щит со всех сторон, его действие уравновешивается, поэтому:

F = ρgh_СS =тρg (Н/2) * Н* в = 1000* 10 * (1,4/2) * 1,4 * 2,6 = 25,5 кН

2. Сила для поднятия щита Т:

Т = G + F*f = 32 + (255 * 0,3) = 39,65 кН

Пример 4

В боковой плоской стенке резервуара с нефтью (ρ =800 кг/м³) имеется круглый люк диаметром d = 0,5 м, закрытый полусферической крышкой. Высота жидкости в резервуаре над осью люка Н = 3м, вакуум на ее свободной поверхности Р_В = 4,9 кПа.

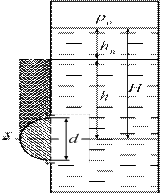Определить горизонтальную и вертикальную составляющие силы давления жидкости на крышку люка, а также величину их равнодействующей и ее направление.

Решение:

1. Найдем положение пьезометрической плоскости, необходимой для определения объема тела давления. Так как на свободной поверхности жидкости – вакуум, пьезометрическая плоскость будет лежать ниже на расстоянии:

h_П = Р_В = 4,9 *10³__ = 0,625 м

ρg 800 *9,81

2. Определим вертикальную составляющую силы давления жидкости на крышку.

Пьезометрическая плоскость лежит выше оси крышки на

h = Н – h_П = 3 – 0,625 = 2,375 м

следовательно, сила давления направлена наружу.

Для верхней половины крышки люка вертикальная составляющая направлена вверх, и ее величина определяется весом тела давления, заштрихованного на рисунке (справа вниз). Объем этого тела давления равен разности объемов полуцилиндра высотой h и четверти шара.

Для нижней половины крышки вертикальная составляющая силы давления направлена вниз. Объем тела давления для этого случая равен сумме объемов полуцилиндра и четверти шара – заштриховано на рисунке (слева вниз).

Результирующая вертикальная сила равна разности этих двух сил, направлена вниз, и объем ее тела давления равен объему жидкости в крышке люка. Поэтому:

F_В = ρgV_Т.Д = 1 ρgπd³ = π 800 * 9,81*0,5³ = 257 Н

12 12

Линия действия этой силы проходит через центр тяжести объема крышки люка на расстоянии от ее основания:

F_Г = 3_ d = 3 *0,5 = 0,094 м

16 16

3. Определим горизонтальную составляющую силы давления жидкости на крышку:

F_Г = ( Р_Т + Р_А)S = ρgh πd² = 800*9,81* 2,375* 3,14* 0.25= 3,65 кН

4 4

Сила направлена параллельно оси Х, а линия ее действия лежит ниже этой оси, на

J__ = πd⁴ 4 _ = d²__ = 0,5²__ = 6,6*10^{-3 м}

ℓ_ТS 64hπd² 16h 16 *2,375

4. Определим равнодействующую сил давления:

_________ _______________________

| F | = √ F_Г² + F_В² = √ (3,65 *10³)² + (0,257 * 10³)² = 3,66 кН

5. Косинус угла α между осью Х и линией действия равнодействующей силы:

сosα = F_Г = 3,65 *10³ = 0,997

|F| 3,66 *10³

Откуда α ≈ 4⁰

Пример 5

После очистки всасывающей линии ( ℓ =10 м, d =200 мм ) насосной установки (КПД η_НАС = 0,65) коэффициент местного сопротивления фильтра ζ_Ф уменьшился от 40 до 10, а эквивалентная шероховатость труб с 1 до 0,1 мм. Подача насоса Q =0,07 м³/с.

Определить годовую экономию электроэнергии от этой операции. Вода имеет t =20 ⁰С (приложение 1).

Решение:

Используя приложение , определим динамическую вязкость воды и ее плотность η = 1мПа*с, ρ = 1000 кг/м³.

1. Определим среднюю скорость воды во всасывающей линии:

υ = Q = 4Q = 4 * 0,07___ = 2,23 м/с

S πd² 3,14 * (0,2)²

2. Определим уменьшение потерь напора в диаметре:

∆h_М.П = h_{М.П 1} – h_{М.П 2} = (ζ₁ – ζ₂ ) υ² = 30 * 2,23 = 7,59 м

2g 19,62

Индексы 1 и 2 относятся к моментам до и после очистки линии.

3. Определим уменьшение потерь напора на трение, используя формулу Дарси – Вейсбаха:

∆h_ТР = h_{ТР 1} – h_{ТР 2} = ( λ₁ – λ₂ ) ℓ * υ² =

d 2g

= ( 0,0273 – 0,0164) 10 * 2,29² = 0,14 м

0,2 19,62

Rе = νdρ = 2,23 * 0,2 * 10³ = 4,46 * 10⁵ – режим турбулентный ˃ 2300

Η 10^-3

Определим зону гидравлических сопротивлений:

500 d = 500 0,2___ = 10⁵ > Rе, поэтому как до, так и после очистки трубы

∆₂ 0,0001 зона сопротивления квадратичная ( ∆₁ ˃ ∆₂ ),

следовательно используем формулу Шифринсона:

λ₁ = 0,11 ( ∆₁/ d)^0,25 = 0,11 ( 0,001/ 0,2)^0,25 = 0,0293

λ₂ = 0.11 ( ∆₂/ d)^0,25 = 0.11 ( 0,0001/0,2)^0,25 = 0,0164

4. Общее уменьшение потерь:

∆h_ПОТ = ∆h_М.П + ∆h_ТР = 7,59 + 0,14 = 7,73 м

5. Вычислим годовую экономию электроэнергии, уменьшение затрат мощности:

∆N = Qρg∆h_ПОТ = 7* 10^-2 *10³ * 9,81* 7,73 = 8,17 кВт

η_НАС 0,65

годовая экономия электроэнергии:

А = ∆N* Т = 8,17 * 10³ * 86,4 * 10³ * 365 = 2,58 * 10¹¹ Вт * с = 71,6 МВт * ч, к

в сутках 864 * 10³ с

Пример 6

Определите расход через сифонный трубопровод, изображенный на рисунке, если высота Н₁ = 1м, Н₂ = 2м, Н₃ = 4м. Общая длина трубы ℓ = 20м, диаметр d = 20 мм. Режим течения считать турбулентным. Учесть потери при входе в трубу ξ₃ =1, в колоннах ξ₂ = 0,2, в вентиле ξ₃ =4м и на трение в трубе

х = 0,035. Подсчитать вакуум в верхнем сечении х-х трубы, если длина участка от входа в трубу до этого сечения ℓ_Х = 8м.

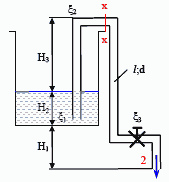Решение:

1.Составим уравнение Бернулли для потока реальной жидкости, для чего выберем сечение 1 и 2, и проведем поверхность сравнения через нижнее сечение z.

2. Определим расход воды:

Q = υs = υ π d² = 1.2 * 3,14 * ( 0,02)² =0,0003 м³/с = 0,38 л/с

4 4

3. Для определения вакуума в сечении х-х составим уравнение Бернулли для сечения 1 и х:

z₁ + Р₁ + α υ₁² = z_Х + Р_Х + α υ_Х² + ∑h_1-Х

ρg 2g ρg 2g

z₁ =0

z_Х = Н₃

Р₁ = Р_АТ = 10⁵ Па

Р_Х = ?

υ₁ = 0

υ_Х = υ₂ = 1,2 м/с

∑h_1-Х = h_{М.П. 1-Х} + h_{ТР 1-Х} = ( λ ℓ_Х + ∑ξ ) * υ₂² = ( 0,035 * 8_+ 1 + 0,2 ) * 1,2² = 1,1м

d 2g 0,02 19,62

Р_АТ = Н₃ + Р_Х + υ₂² + ∑h_{1- Х}

ρg ρg 2g

Р_Х = ( Р_АТ – Н₃ – υ₂² - ∑h_1-Х) ρg = ( 10 – 4 – 0,072 – 1,1 ) * 10⁴ = 0,48 * 10⁵ Па

ρg 2g

Р_ВАК = Р_АТМ – Р_АБС = Р_АТМ – Р_Х = 1* 10⁵ – 0,48* 10⁵ = 0,52* 10⁵Па ≈ 0,052 МПа

Пример 7

Насос, оборудованный воздушным колпаком, перекачивает бензин по трубопроводу длиной ℓ = 5 км, диаметром d = 75 мм, δ = 5мм в количестве

Q = 9 * 10^-3 м³/с. Плотность бензина ρ = 740 кг/м³, модуль упругости бензина

К = 1,1* 10⁹ Па, Е = 2* 10¹¹ Па.

Определите, за какое время необходимо перекрыть задвижку, чтобы ударное повышение давления не превосходило ∆Р = 1 МПа.

Решение:

1. Определим скорость движения бензина:

υ = 4Q = 4* 9 * 10^-3__ = 2,04 м/с

πd² 3,14 * 0,075²

2. Определим скорость волны гидравлического удара:

___ ________

|К * ____1____ = | 1,1 * 10⁹ *____1__________ = 1.22 * 10³ =1,17*10³м/с

С=√ ρ | 1 + К * d √ 7,4 *10² | 1 + 1,1 * 10⁹* 75 1,04

√ Е δ √ 2 * 10¹¹ * 5

3. Повышение давления при прямом гидравлическом ударе:

∆Р = ρСυ = 740 * 1,17 * 10³* 2,04= 1,77 МПа ˃ 1 МПа, следовательно гидравлический удар непрямой.

4. Фаза удара, то есть время пробега волны от задвижки до воздушной колонны и назад:

Т = 2ℓ = 10⁴____ = 8,55 с

С 1,17* 10³

5. Необходимое время закрытия задвижки:

t = ρСυ * Т = 1,77 * 10⁶ *8,55 = 15 с

∆Р 10⁶

Пример 8

В центре кругового пласта ( R_К = 1 км, h = 10 м, k= 0,5 мкм², m = 0,2)

Расположение скважины r_С = 0,1 м, глубина Н = 2000м. Вязкость нефти

η = 10^-2 Па*с, плотность ρ = 870 кг/м³, абсолютное пластовое давление

Р_ПЛ = 20 МПа.

Необходимо определить, может ли скважина фонтанировать, если ее открыть в атмосферу, и, чему равен ее дебит при Р = 19 МПа?

Решение:

1. Если скважину открыть в атмосферу , то жидкость в ней сможет подняться на высоту:

Н_С = Р_ПЛ = 19,9 * 10⁶ = 2332 м

ρg 870 * 9,81

где Р_ПЛ.ИЗБ = Р_ПЛ – Р_АТМ = (20 – 0,1)МПа = 19,9 МПа, так как Н_С ˃ Н, то

скважина будет фонтанировать

2. Дебит скважины определим по формуле Дюпюи:

Q = 2πkh * Р_К - Р_С = 2*3,14*5*10^-13*10 *20*10⁶ – 19*10⁶ =3,41*10^-4 м³/с=29,5м³/сут

η ℓn R_К 10^-2 9,21

r_С

КОНТРОЛЬНАЯ РАБОТА

ВАРИАНТ 1

1. Какое физическое тело называется жидкостью?

2. Каково условие выноса твердых тел восходящим потоком жидкости?

Задачи: 4,9,18,20,33.

ВАРИАНТ 2

1. Как определяется сила сопротивления тел при их обтекании?

2. В чем отличие между реальной и идеальной жидкостями?

Задачи: 1, 14, 16, 21,30

ВАРИАНТ 3

1. Что называется плотностью жидкости? Каковы единицы измерения

плотности жидкости? Какие факторы и как влияют на плотность?

2. От каких факторов зависит величина коэффициента гидравлического

сопротивления?

Задачи: 2, 5, 7, 22, 31.

ВАРИАНТ 4

1. Что называется эквивалентной длиной местного сопротивления?

2. Чем характеризуется сжимаемость и температурное расширение капельной жидкости?

Задачи: 3, 8, 17, 23, 32.

ВАРИАНТ 5

1. Что называется давлением насыщения паров жидкости и от чего зависит

его величина?

2. Каково влияние вязкости жидкости и диаметра трубопровода на потери

напора в нем?

Задачи: 6, 10, 19, 24, 33

ВАРИАНТ 6

1. Каковы законы распределения местных скоростей в живом сечении

потока при ламинарном и турбулентном режимах?

2. Что называется вязкостью жидкости и от чего она зависит?

Задачи: 4, 10, 18, 25, 34.

ВАРИАНТ 7

1. Каковы единицы измерения динамической и кинематической вязкости и

какова их взаимосвязь?

2. Каковы основные расчетные формулы для определения λ при

турбулентном режиме?

Задачи: 1, 11, 17, 26, 35.

ВАРИАНТ 8

1. В чем заключаются опыты Никурадзе и каковы их результаты?

2. Как называются приборы для измерения плотности и вязкости жидкости? Принцип их действия?

Задачи: 2, 12, 18, 27, 30.

ВАРИАНТ 9

1. Что называется гидростатическим давлением, в каких единицах оно

измеряется? Укажите их взаимосвязь.

2. Какие шероховатости называются эквивалентной и относительной?

Задачи: 3, 13, 19, 28, 31.

ВАРИАНТ 10

1. Что такое осредненная во времени местная скорость жидкости при

турбулентном потоке?

2. Какое давление называется избыточным, какое вакуумом?

Задачи: 4, 14, 20, 29, 32.

ВАРИАНТ 11

1. Каковы основные свойства гидростатического давления?

2. Что определяется по формуле Дарси – Вейсбаха, и как она записывается?

Задачи: 5, 15, 21, 28, 33.

ВАРИАНТ 12

1. Как определяется число Рейнольдса и чему равно его критическое

значение для труб различного сечения?

2. Как формулируется закон Паскаля?

Задачи: 6, 14, 19, 27, 34.

ВАРИАНТ 13

1. Как записывается основной закон гидростатики? В каких единицах измеряются величины, входящие в него?

2. Какое движение называется установившимся, какое медленно изменяющимся?

Задачи: 1, 13, 18, 26, 35.

ВАРИАНТ 14

1. Что называется живым сечением?

2. Какая поверхность называется пьезометрической?

Задачи: 2, 12, 17, 25, 34.

ВАРИАНТ 15

1. Чем дифференциальный жидкостной манометр отличается от простого и

как по его показаниям можно определить разность давлений в точках

подключения такого манометра?

2. Как определяется средняя скорость потока, если известен объемный

расход жидкости?

Задачи: 3, 11, 22, 28, 33.

ВАРИАНТ 16

1. Что называется гидравлическим радиусом потока?

2. В чем преимущества и недостатки механических манометров по сравнению с жидкостными?

Задачи: 4, 10, 17, 27, 32.

ВАРИАНТ 17

1. Как определяется результирующая сила давления жидкости на плоскую

поверхность?

2. Запишите уравнении Бернулли для потока реальной жидкости. Что

представляют из себя составляющие части этого уравнения?

Задачи: 5, 9, 19, 23, 31.

ВАРИАНТ 18

1. Каков физический смысл членов, входящих в уравнение Бернулли?

2. Что называется центром давления и как определяется его координата ℓ_Д?

Задачи: 6, 10, 20, 24, 32.

ВАРИАНТ 19

1. Как определить горизонтальную и вертикальную составляющие силы

давления жидкости на криволинейную поверхность?

2. Что называется гидравлическим уклоном?

Задачи: 1, 11, 21, 25, 33.

ВАРИАНТ 20

1. Назовите два вида потерь напора. Каковы принципы сложения потерь

напора?

2. Каково устройство и принцип действия гидравлического пресса?

Задачи: 2, 12, 22, 26, 34.

ВАРИАНТ 21

1. Что называется телом давления? Реальное и фиктивное тело давления.

В чем разница?

2. Почему в расходомере Вентури давление в узком сечении меньше, чем в

широком?

Задачи: 3, 13, 23, 27, 35.

ВАРИАНТ 22

1. Каково принципиальное устройство скоростной трубки Прандтля и что

она измеряет?

2. Как формулируется закон Архимеда?

Задачи: 4, 14, 24, 28, 34.

ВАРИАНТ 23

1. В чем заключается гидростатический парадокс?

2. По какой формуле определяется полезная мощность насоса?

Задачи: 5, 15, 25, 29, 33.

ВАРИАНТ 24

1. Выведите и запишите основное уравнение гидростатики

2. Какие трубопроводы называют сложными и каковы их основные типы?

Задачи: 6, 8, 18, 28, 32.

ВАРИАНТ 25

1. Какие формулы применяются для расчета трубопроводов?

2. Как изменяются коэффициент сжимаемости β_v и коэффициент температурного расширения β_t с изменением давления и температуры?

Задачи: 1, 7, 17, 27, 31.

ВАРИАНТ 26

1. Как записать уравнение баланса напоров в случае, если жидкость по

трубопроводу перекачивается насосом?

2. Дайте определение поверхностному натяжению. Опишите механизм возникновения давления поверхностного натяжения.

Задачи: 2, 9, 19, 29, 30.

ВАРИАНТ 27

1. Что такое гидравлический удар и каковы условия его возникновения?

2. Запишите формулу Менделеева для определения плотности жидкости

Задачи: 3, 10, 21, 28, 31.

ВАРИАНТ 28

1. Как определить удельный вес жидкости? Чем он отличается от

плотности жидкости?

2. Опишите явление кавитации.

Задачи: 4, 11, 17, 26, 32.

ВАРИАНТ 29

1. Каково условие работы трубопровода, работающего под вакуумом?

2. Что такое параллельно- прямолинейная фильтрация жидкости и каков закон Дарси для нее?

Задачи: 5, 12, 18, 22, 33.

ВАРИАНТ 30

1. Запишите формулу Дюпюи для несжимаемой жидкости. Опишите

каждую величину, входящую в эту формулу.

2. Каковы качественные характеристики насадков различного вида и

области их применения?

Задачи: 6, 15, 19, 29, 34.

Задача №1

Канистра, заполненная жидкостью и не содержащая воздуха, нагрелась на солнце до температуры t₂.

На сколько повысилось бы давление жидкости внутри канистры, если бы она была абсолютно жесткой?