Элементы линейной алгебры и аналитической геометрии

Федеральное государственное бюджетное

Образовательное учреждение

Высшего образования

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Филиал УГНТУ в г. Октябрьский

Кафедра информационных технологий,

математики и естественных наук

«Высшая математика»

учебно-методическое пособие

для студентов заочного отделения

Уфа

В учебно – методическом пособии приводятся образцы решений задач, подобных вариантам заданий контрольной работы, и варианты контрольных заданий для студентов заочной формы обучения всех специальностей.

Составители: Игтисамова Г.Р., доц., канд. пед. наук

Ихсанова Ф.А., ст. преподаватель

Ларин П.А., ст. преподаватель

Усманова Ф.К., ст. преподаватель

Рецензент Тынчеров К. Т. проф., д-р техн.наук

© Уфимский государственный нефтяной технический университет, 2012

ВВЕДЕНИЕ

Дисциплина «МАТЕМАТИКА» лежит в основе фундаментальной подготовки, как специалистов, так и бакалавров, независимо от будущей специальности выпускника, и составляет базовую часть образовательной программы математического и естественно-научного цикла дисциплин. Фундаментальная подготовка и, в частности, математическое образование необходимо для успешной профессиональной деятельности, для возможности самостоятельного приобретения знаний в новых областях науки и техники, самостоятельного повышения квалификации, адекватного восприятия и использования новой информации.

Математика является основой для развития логического мышления, для формирования обоснованных суждений по профессиональным, научным и этическим вопросам, для умения научно анализировать проблемы и процессы в профессиональной области, умения ставить задачи и находить способы их решения, а также для грамотной интерпретации полученных результатов.

Математика дает не только универсальную базу для изучения общепрофессиональных и специальных дисциплин, но также надежный аппарат изучения в дальнейшем сложных систем в любой предметной области, дает аппарат для моделирования, анализа и синтеза, прогноза и диагностики функционирования таких систем, создания и эксплуатации новых сложных систем.

Основными целями изучения дисциплины «Математика» являются:

- развитие логического мышления;

- повышение уровня математической культуры;

- овладение современным математическим аппаратом, необходимым для изучения естественнонаучных, общепрофессиональных и специальных дисциплин;

- освоение методов математического моделирования.

ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПО РАБОТЕ НАД КУРСОМ МАТЕМАТИКИ

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В помощь заочникам институты организуют чтение лекций, практические занятия и лабораторные работы. Кроме того, студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь университета будет достаточно эффективной. Завершающим этапом изучения отдельных частей курса математики является сдача зачетов и экзаменов в соответствии с учебным планом.

Чтение учебника

1.1. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, выполняя на бумаге все вычисления (в том числе те, которые ради краткости опущены в учебнике) и вычерчивая имеющиеся в учебнике чертежи.

1.2. Особое внимание следует обращать на определения основных понятий. Студент должен подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно.

1.3. Необходимо помнить, что каждая теорема состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательств сложных теорем. Правильному пониманию многих теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в предположениях и утверждениях теорем.

1.4. При изучении материала по учебнику полезно вести конспект, в который рекомендуется выписывать определения, формулировки теорем, формулы, уравнения и т.п. На полях конспекта следует отмечать вопросы, выделенные студентом для получения письменной или устной консультации преподавателя.

1.5. Письменное оформление работы студента имеет исключительно важное значение. Записи в конспекте должны быть сделаны чисто, аккуратно и расположены в определенном порядке. Хорошее внешнее оформление конспекта по изученному материалу не только приучит студента к необходимому в работе порядку, но и позволит ему избежать многочисленных ошибок, которые происходят из-за небрежных, беспорядочных записей.

1.6. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой, чтобы при перечитывании конспекта они выделялись и лучше запоминались. Опыт показывает, что многим студентам помогает в работе составление листа, содержащего важнейшие и наиболее часто употребляемые формулы курса. Такой лист не только помогает запомнить формулы, но и может служить постоянным справочником для студента.

Решение задач

2.1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.

2.2. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса. Если студент видит несколько путей решения, то он должен сравнить их и выбрать из них самый лучший. Полезно до начала вычислений составить краткий план решения.

2.3. Решения задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения, например при графической проверке решения, полученного путем вычислений, то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб.

2.4. Решение каждой задачи должно доводиться до ответа, требуемого условием, и по возможности в общем виде с выводом формулы. Затем в полученную формулу подставляют числовые значения (если таковые даны). В промежуточных вычислениях не следует вводить приближенные значения корней, числа 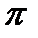и т.п.

Контрольные работы

3.1. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы, желательное направление дальнейшей работы; помогают сформулировать вопросы для постановки их перед преподавателем.

3.2. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания объясняется тем, что студент не выполнил это требование.

3.3. Контрольные работы должны выполнять самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться не подготовленным к устному зачету и экзамену.

3.4. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированных контрольных работ студент не допускается к сдаче зачета и экзамена.

СОДЕРЖАНИЕ КУРСА «МАТЕМАТИКА»

I СЕМЕСТР

Элементы линейной алгебры и аналитической геометрии

Вектор. Линейные операции над векторами. Базисы на плоскости и в пространстве. Декартова система координат. Проекции и координаты вектора. Скалярное и векторное произведение векторов. Условие ортогональности, коллинеарности и компланарности векторов. Смешанное произведение.

Прямая линия на плоскости. Плоскость и прямая в пространстве. Кривые и поверхности второго порядка.

Матрицы и действия над ними. Определители. Их свойства. Обратная, транспонированная и ортогональная матрицы, их свойства. Обратная матрица, решение матричных уравнений. Ранг матрицы. Теорема о базисном миноре.

Системы линейных уравнений. Правило Крамера, метод Гаусса.