Неопределенный интеграл
1. Понятие первообразной и неопределенного интеграла.
2. Свойства неопределенного интеграла.
3. Таблица интегралов.
4. Теорема об инвариантности формы интегрирования.
5. Интегрирование методом замены переменной.
6. Интегралы вида: 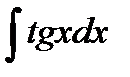 ,
, 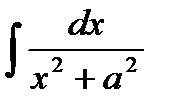 ,
, 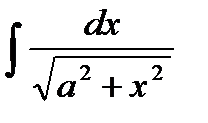 ,
, 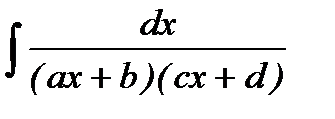 .
.
7. Интегрирование по частям. Основные случаи интегрирования по частям.
8. Интегрирование функций, содержащих квадратный трехчлен: 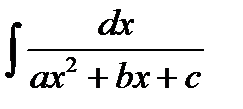 ,
, 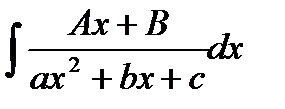 .
.
9. Интегрирование функций, содержащих квадратный трехчлен: 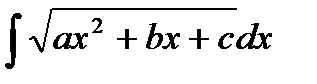 .
.
10. Интегрирование функций, содержащих квадратный трехчлен: 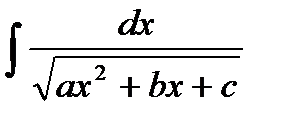 ,
, 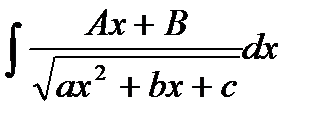 .
.
11. Представление дробно-рациональных функций в виде простейших дробей.
12. Интегрирование простейших дробей: 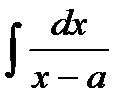 ,
, 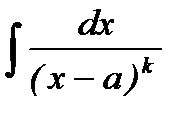 ,
, 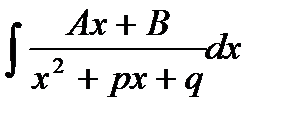 ,
, 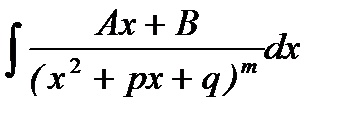 .
.
13. Интегрирование иррациональных функций вида: 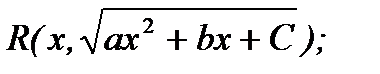
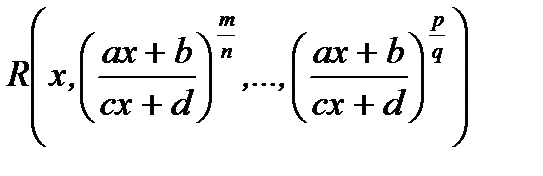 ,
, 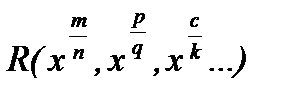 .
.
14. Интегрирование дифференциального бинома: 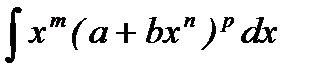 .
.
15. Интегрирование выражений содержащих тригонометрические функции. Универсальная замена.
16. Теорема об интегрировании функций, нечетных относительно 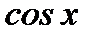 или
или 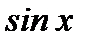 .
.
17. Теорема об интегрировании функций, четных относительно 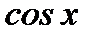 или
или 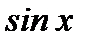 .
.
18. Интегрирование выражений вида: 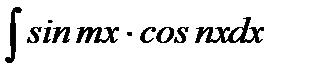 ,
, 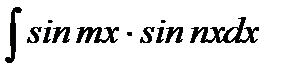 ,
, 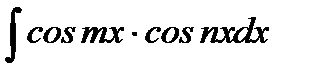 ,
, 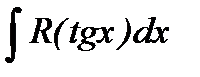 .
.
19. Понятие «не берущийся интеграл».
Определенный интеграл
20. Задачи, приводящие к понятию определенного интеграл: а) вычисление площади криволинейной трапеции; б) работа переменной силы.
21. Определенный интеграл. Определение. Теорема существования определенного интеграла (без доказательства).
22. Свойства определенного интеграла. Интеграл от суммы функций, вынесение постоянного множителя за знак интеграла, совпадение знака интеграла со знаком подынтегральной функции.
23. Свойства определенного интеграл. Теорема о перестановке пределов интегрирования, о разбиении интеграла, об оценке определенного интеграла, теорема о среднем.
24. Теорема о производной интеграла по верхнему пределу интегрирования.
25. Формула Ньютона Лейбница, связь определенного интеграла с неопределенным.
26. Замена переменной в определенном интеграле.
27. Интегрирование по частям в определенном интеграле.
28. Геометрические приложения определенного интеграла: вычисление площадей фигур.
29. Геометрические приложения определенного интеграла: вычисление длин дуг в различных системах координат.
30. Геометрические приложения определенного интеграла: вычисление объема тел по известным площадям поперечных сечений и объем тел вращения.
31. Вычисление работы при помощи определенного интеграла.
32. Несобственные интегралы: а) с бесконечными пределами; б) от разрывной функции. Рассмотреть случай: 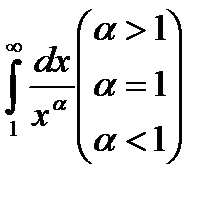 .
.
33. Приближенное вычисление определенного интеграла: а) формула трапеции; б) формула парабол (формула Симпсона) с доказательством леммы.
контрольная работа № 2
Контрольная работа № 4 состоит из пяти заданий. Ниже подробно рассмотрены варианты решения заданий.
