Тригонометрические ряды
1. Достаточное условие разложимости функции в ряд Фурье. Кусочно - монотонные функции.
2. Ряд Фурье для четных и нечетных функций.
3. Ряд Фурье для функции с периодом 2е.
4. Разложение в ряд Фурье функций, заданных на полупериоде.
КОНТРОЛЬНАЯ РАБОТА № 7
Контрольная работа № 7 состоит из пяти задач. Ниже рассмотрены варианты решения заданий.
Образец выполнения задания № 1
Задача.Найти общее решение уравнения 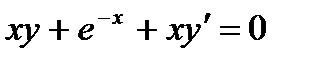 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию 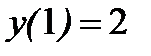 .
.
Решение. Преобразуем уравнение: 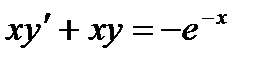 ,
, 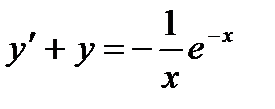 . Это линейное уравнение 1 порядка. Сделаем замену
. Это линейное уравнение 1 порядка. Сделаем замену 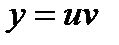 .
.
Тогда 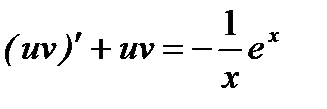 ,
, 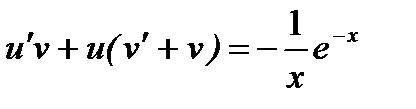 .
.
Составим систему 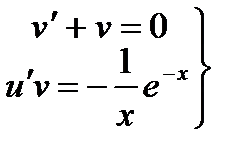 .
.
Решаем первое уравнение: 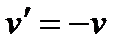 ,
, 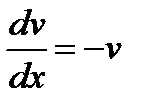 ,
, 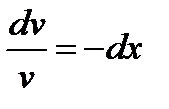 ,
, 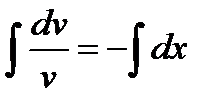 ,
, 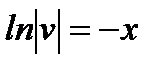 (при решении этого уравнения постоянную интегрирования
(при решении этого уравнения постоянную интегрирования  можно не писать),
можно не писать), 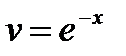 . Подставим во второе уравнение,
. Подставим во второе уравнение, 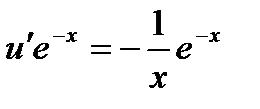 и решим его.
и решим его.
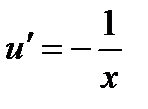 ,
, 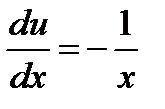 ,
, 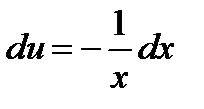 ,
, 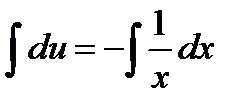 ,
, 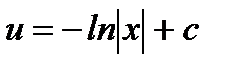 .
.
Следовательно, 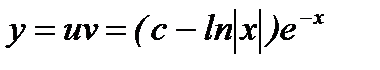 - общее решение дифференциального уравнения. Для нахождения частного решения применим условия
- общее решение дифференциального уравнения. Для нахождения частного решения применим условия 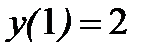 , т.е. подставим
, т.е. подставим 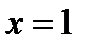 ,
, 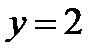 в общее решение:
в общее решение: 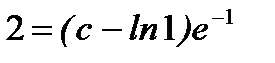 , отсюда
, отсюда 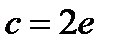 .
.
Значит 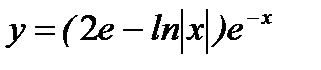 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Образцы выполнения заданий № 2
Задача 1.Найти общее решение уравнения 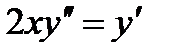 и частное решение, удовлетворяющее начальным условиям:
и частное решение, удовлетворяющее начальным условиям: 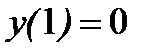 ,
, 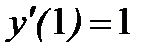 .
.
Решение. Уравнение 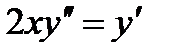 не содержит
не содержит 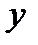 , поэтому делаем замену
, поэтому делаем замену 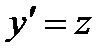 (
( 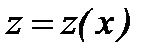 ). Тогда
). Тогда 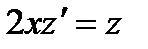 ,
, 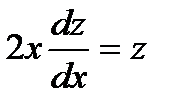 ,
, 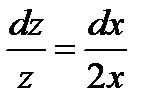 ,
, 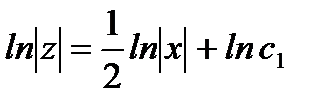 ,
, 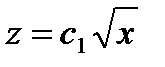 ,
, 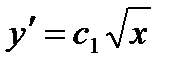 ,
, 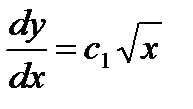 ,
, 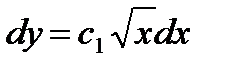 ,
, 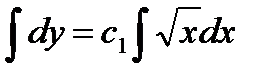 ,
, 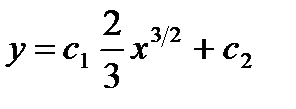 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Чтобы найти частное решение, используем начальные условия. Имеем
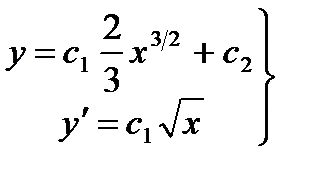 отсюда
отсюда 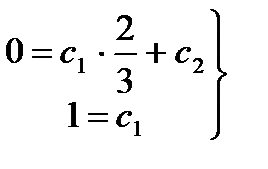
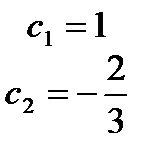
Значит, искомое частное решение таково:  .
.
Задача 2.Найти общее решение уравнения 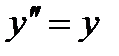 и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям 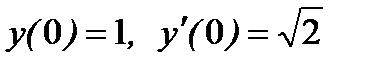 .
.
Решение. Уравнение 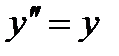 не содержит
не содержит 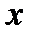 , поэтому делаем замену
, поэтому делаем замену 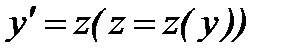 . Тогда
. Тогда 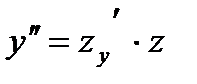 ,
, 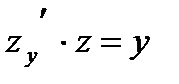 ,
, 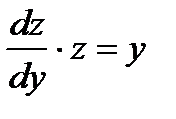 ,
, 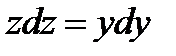 ,
, 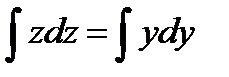 ,
, 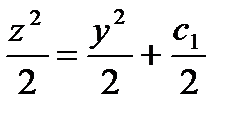 ,
, 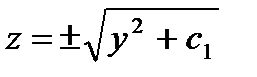 или
или 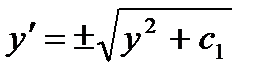 ,
, 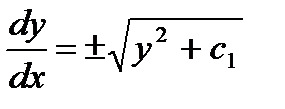 ,
, 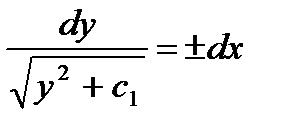 ,
, 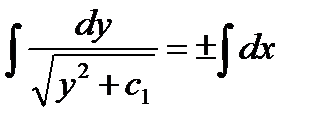 ,
, 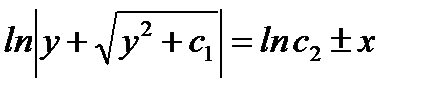 ,
, 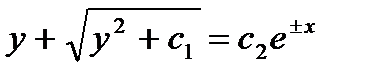 = общее решение дифференциального уравнения.
= общее решение дифференциального уравнения.
Переходим к нахождению частного решения. Имеем
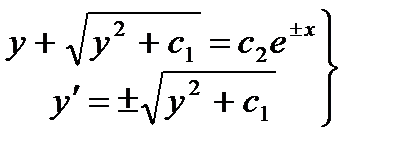
Подставив сюда начальные условия, получим
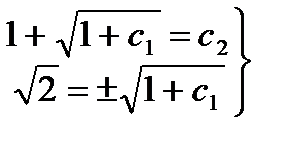
Второе равенство удовлетворяется, если взять знак «+». Тогда 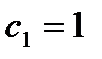 ,
,  .
.
Отсюда 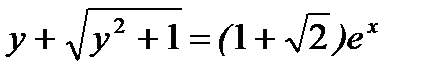 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Образец выполнения задания № 3
Задача.Найти частное решение дифференциального уравнения 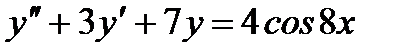 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 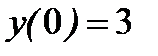 ,
, 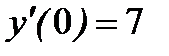 .
.
Решение. Сначала найдем общее решение 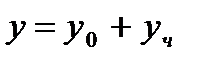 , где
, где 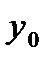 - решение соответствующего однородного уравнения,
- решение соответствующего однородного уравнения, 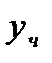 - частное решение.
- частное решение.
Составляем характеристическое уравнение 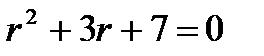 и находим его корни
и находим его корни 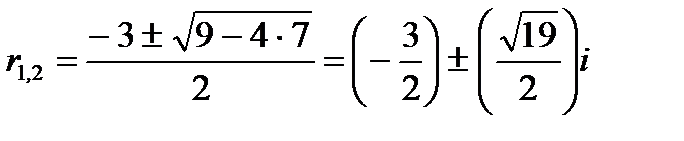 , где
, где 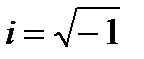 - минимальная единица.
- минимальная единица.
Отсюда 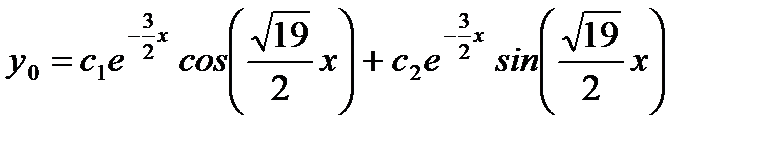 .
.
Частное решение ищем в таком виде, который соответствует правой части исходного уравнения, а именно 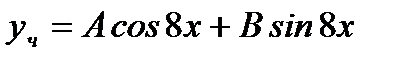 .
.
Чтобы найти А, В, подставим это выражение в исходное уравнение
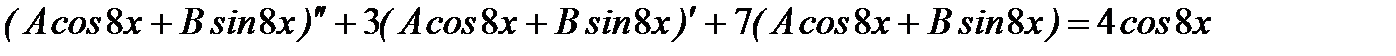 .
.
Вычислив производные и упростив левую часть, получим
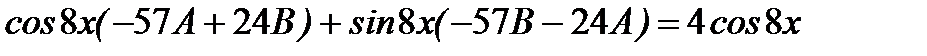 , отсюда будем иметь систему
, отсюда будем иметь систему
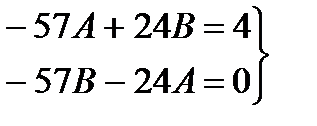 , решение которой
, решение которой 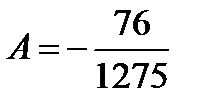 ,
, 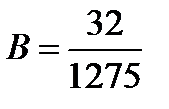 .
.
Следовательно, 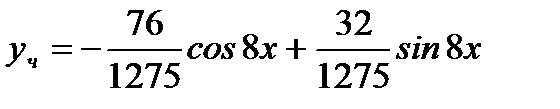 ,
,
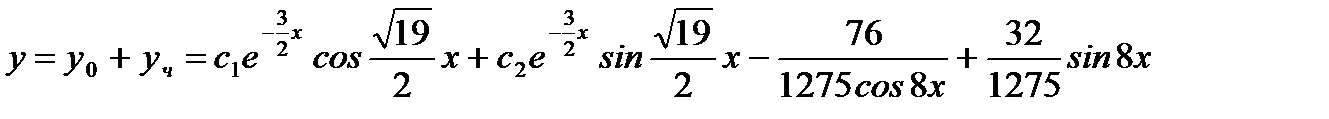 .
.
Производная этой функции равна
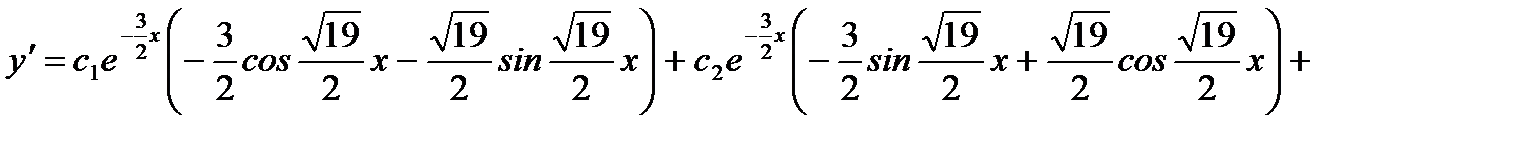
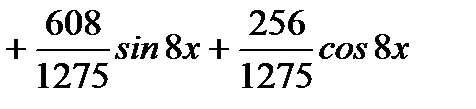 .
.
Подставим начальные условия: при 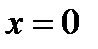 ,
, 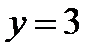 ,
, 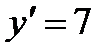 . Получим
. Получим
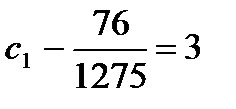 ,
, 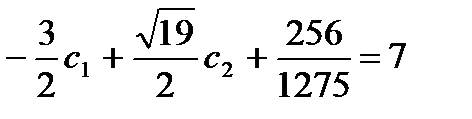 , отсюда
, отсюда 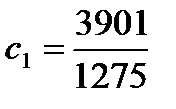 ,
, 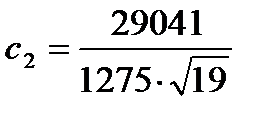 .
.
Ответ. Частное решение таково:
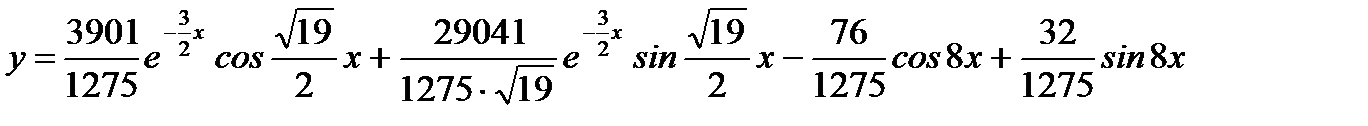 .
.
