Некоторые примеры линий, заданных неявно, исследование которых проводится на основе обычной школьной программы

Пример 1. Построить кривую: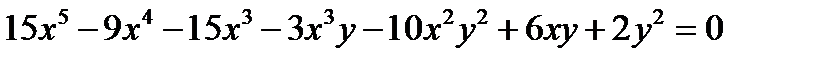

Решение. Данное уравнение можно преобразовать к виду

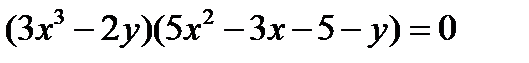
и потом представить как 2 уравнения:

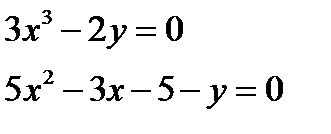
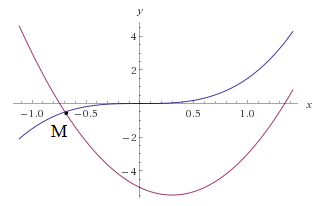Рисунок 10

или в виде:

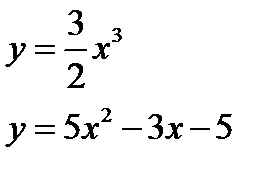
Построить графики этих двух функций не является большой проблемой (рис. 10). Точка М – точка самопересечения (узел)

Пример 2. Построить кривую: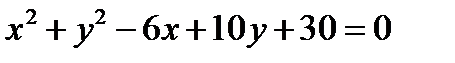

Данное уравнения можно привести к виду: 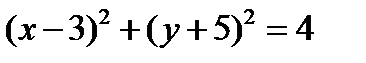, что является окружностью с центром в точке С(3; -5) и радусом 2 (рис. 11).

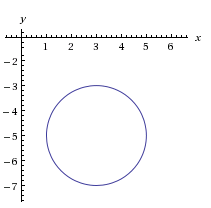	Рисунок 11

Пример 3. Построить кривую: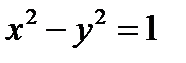

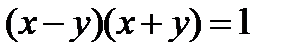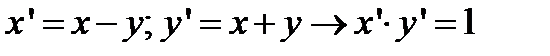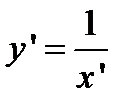Выполним преобразование: . Потом введем обозначение или - гипербола (рис. 12)

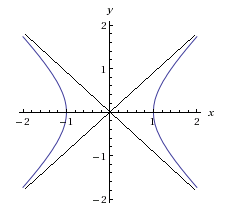	Рисунок 12

Линии второго порядка, заданные неявно

Существует 9 типов линий второго порядка. Все они представлены ниже.

1. 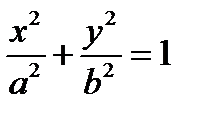- эллипс

2. 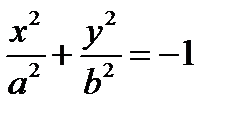- мнимый эллипс

3. а) 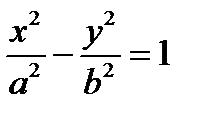, б) 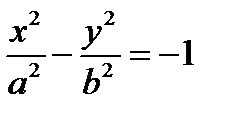- гиперболы

4. 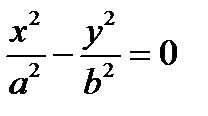- пара пересекающихся прямых

5. 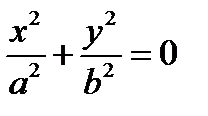- пара мнимых пересекающихся прямых

6. 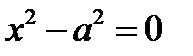- пара параллельных прямых

7. 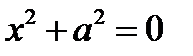- пара мнимых параллельных прямых

8. 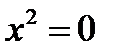- пара совпавших прямых

9. а) 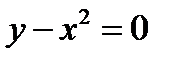, б) 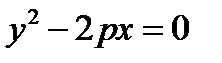- параболы

Замечание. Линия 1 рассмотрена в приложении 2.

Линии 4, 6, 8, 9 рассматриваются в обычном школьном курсе математики

4.3. Исследование линий, заданных неявно, на основе теории, рассмотренной в §3 главы I

Здесь в спецкурс можно включить задачи типа 1, 4, 5 §4 главы I, или задачи типа примера 1, пункта 1.4, где, выполнив дополнительные исследования, можно показать, что точка М – точка самопересечения.

Заключение

В данной работе рассмотрены только отдельные вопросы теории кривых. Понятно, что следовало бы разработать отдельно следующие темы:

1) Некоторые вопросы топологии в школьном курсе математики

2) Исследование линий, заданных параметрически

3) Разработать уроки на тему: «линии второго порядка, заданные неявно»

4) Приложение данной теории в физике

5) Привести большее число задач, иллюстрирующих данную теорию

Приложение А

Примерный план спецкурса «Исследование линий на плоскости, заданных явно и неявно»

Номер	Тема	Часы
1.1   1.2 1.3 1.4 1.5 1.6 1.7	Некоторые вопросы топологии в школьном курсе математики Понятие линии (кривой) на топологической основе Различные способы задания плоской кривой Явное и неявное задание функции Введение понятия частной производной Исследование линий, заданных явно Исследование линий, заданных неявно
	Итого

Замечание:данный спецкурс можно разбить на 2 части: 1 часть – 9 класс (темы: 1.1 (3 часа), 1.2 (2 часа), 1.3 (2 часа), 1.4 (2 часа), 1.6 (2 часа), 1.7 (4 часа)). Остальные вопросы можно рассмотреть в 10-11 классах.

Приложение Б

Здесь в качестве примера мы рассмотрим теоретическую часть одного из возможных уроков.

Замечание: Даная тема рассматривается в 9 классе (когда изучены темы: окружность, синус и косинус угла, симметрия), может служить хорошей основой для последующего изучения тем в математике (параллельное проектирование, изображение круглых тел и т.п.) и в физике.

План – конспект урока

Класс: 9 класс

Тема: Эллипс

Цель урока: Дать основные понятия и свойства эллипса

Задачи:

Общеобразовательные: расширение понятийной базы по учебному предмету за счет включения в нее новых элементов

Развивающие: развивать в учениках математическую культуру, логическое мышление.

Воспитательные: создать интерес учащихся к науке, вне школьной программы.

Дидактическое оснащение урока: доска, план-конспект, письменные принадлежности.

Краткий план урока:

Содержание урока

1. Начало урока. Организационный момент. Объявление темы урока.

2. Основная часть урока.

Речь учителя: Как мы знаем из школьного курса, окружность - замкнутая кривая, все точки которой равно удалены от центра. Но окружность является частным случаем эллипса.

Эллипс – множество всех точек плоскости, для каждой из которых сумма расстояний до точек F₁, F₂ той же плоскости есть величина постоянная. Где точки F₁, F₂ – фокусы эллипса, а расстояние между ними – фокальное расстояние.

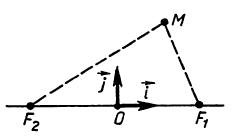Рисунок 1

Фокальными радиусами т. М называются отрезки F₁M, F₂M, если M – точка данного эллипса.

Найдем уравнение эллипса в прямоугольной системе координат 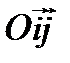, где О – середина отрезка F₁F₂, а 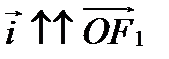(рис.1).

В выбранной системе координат фокусы F₁ F₂ эллипса имеют координаты F₁(c,0), F₂(-c,0), поэтому фокальные радиусы произвольной точки М(х, у) эллипса равны:

.

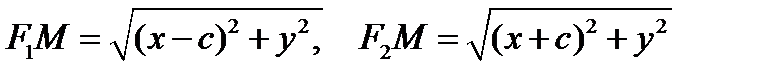(1)

Т.к. F₁M+F₂M=2a, поэтому 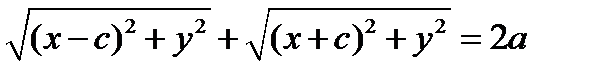или в другом виде 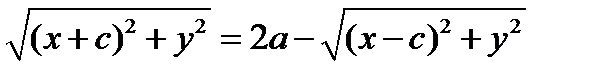. Возводя его в квадрат и приводя подобные члены, получим: 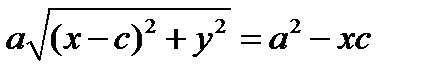. Снова возводя в квадрат, после преобразований получим

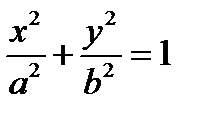(2)

где 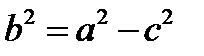(3).

Таким образом, мы доказали, что координаты любой точки эллипса удовлетворяют уравнению (2). Уравнение (2) называется каноническим уравнением эллипса.

Рассмотрим свойства эллипса.

Если 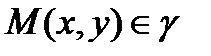, то 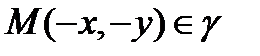, поэтому т. О – центр симметрии эллипса

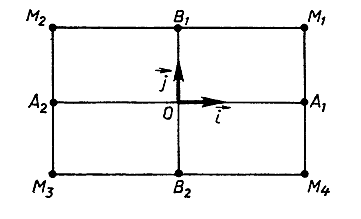Рисунок 2

Если 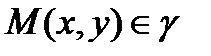, где 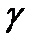- эллипс, то х, у удовлетворяют уравнению (2), поэтому 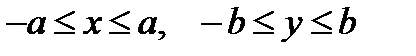, т.е. все точки эллипса принадлежат прямоугольнику М₁М₂М₃М₄ (рис. 2)

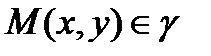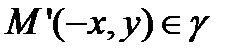Если , то и 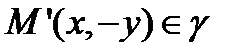. Отсюда следует, что прямые Ох и Оу являются осями симметрии эллипса.

Каждая ось симметрии пересекается с эллипсом в двух точках: 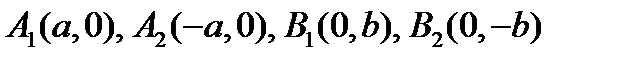. Эти точки называются вершинами симметрии(рис. 2). Отрезки A₁A₂ и B₁B₂ называются большой и малой осями эллипса, соответственно. Центр О является серединой отрезка.

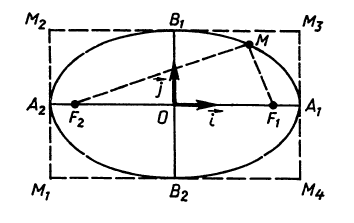Рисунок 3

Чтобы получить представление о виде эллипса, заданного уравнением (2), следует построить несколько точек эллипса. При этом достаточно рассмотреть только точки первой четверти, т.к. эллипс симметричен относительно осей координат. Для точки M (x, y) первой четверти ( 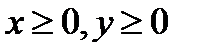) имеем: 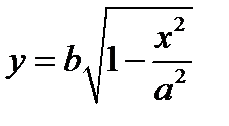(рис. 3).

Эксцентриситетом эллипса называется число 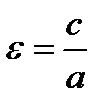, где с – фокальное расстояние, а – большая полуось, т.е. 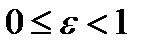. 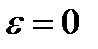только тогда, когда эллипс – окружность, т.е. с = 0.

С увеличением эксцентриситета уменьшается «ширина» эллипса.

Из определения и свойств перечисленных выше следует способ построения эллипса.

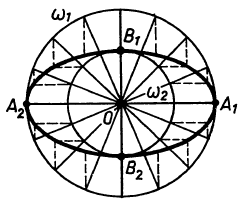Рисунок 6

Рассмотрим способ построения точек эллипса с помощью циркуля и линейки, если заданы его оси A₁A₂ и B₁B₂. На отрезках A₁A₂ и B₁B₂ как на диаметрах построим две концентрические окружност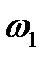и и 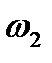(рис. 6). Проведем ряд радиусов большей окружности. Через их концы проведем прямые, параллельные малой оси, а через точки пересечения этих радиусов с меньшей окружностью – прямые, параллельные большей оси. Тогда точки пересечения прямых, соответствующих одному и тому же радиусу, будут точками эллипса с заданными осями.

3. Завершение урока.

Таким образом, на сегодняшнем занятии мы рассмотрели основные определения эллипса и некоторые его свойства.

Список литературы

1. Александров, Н. В. Курс общей физики. Механика: учеб. пособие / Н. В. Александров, А.Я. Яшкин. – М.: Просвещение, 1978. – 416с.

2. Алимов, Ш.А. Алгебра и начала математического анализа. 10-11 классы / Ш.А. Алимов [и др.]. – М.: Просвещение, 2012. – 464 с.

3. Атанасян, Л.С. Геометрия. 7-9 классы. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев – М.: Просвещение, 2014. – 383с.

4. Барский, И. Б. Элементы общей топологии и теории топологических многообразий: учеб. пособие / И. Б. Барский. – Йошкар-Ола: Марийский государственный университет, 2011. – 224с.

5. Колмогоров, А.Н. Алгебра и начала математического анализа. 10-11 классы. / А.Н. Колмогоров, А.М [и др.]. – М.: Просвещение, 2008. – 384 с.

6. Мордкович, А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч., Ч.1 / А.Г. Мордкович [и др.]. – М.: Мнемозина, 2013. –400с.

7. Погорелов, А.В. Геометрия. 7-9 классы. / А.В. Погорелов – М.: Просвещение, 2014. – 240с.

8. Погорелов, А.В. Геометрия / А.В. Погорелов. – М.: Наука, 1983. – 290с.

9. Саранцев, Г.И. Методика обучения геометрии: учеб. пособие для студентов ВУЗов по направлению "Педагогическое образование" / Саранцев Г.И. – Казань.: Центр инновационных технологий, 2011. – 228с.

10. Феденко, А.С. Сборник задач по дифференциальной геометрии: учеб. пособие / А.С. Феденко [и др.]. – М.: Наука, 1979. – 272с.

11. Фиников, С.П. Дифференциальная геометрия. Методическое пособие для студентов педагогических институтов: учеб. пособие / С.П. Фиников. – М.: Учпедгиз, 1949. – 109с.

12. Фиников, С.П. Дифференциальная геометрия: учеб. пособие / С.П. Фиников. – М.: Учпедгиз, 1955. – 215с.

13. Фихтенгольц, Г.М. Основы математического анализа. Т.1. / Г.М. Фихтенгольц – М.: Наука, 2005. – 440с.