Методика и порядок выполнения работы. 5.1Прогноз произвести на примере выпуска продукции предприятием (таблица 5.1).
5.1Прогноз произвести на примере выпуска продукции предприятием (таблица 5.1).
| № квартала, t | Потребление электроэнергии, Уi (№ варианта) | ||||||||||
| 15,1 | 12,1 | 12,8 | 13,6 | 15,9 | 16,6 | 17,4 | 18,1 | 18,9 | 11,3 | ||
| 16,5 | 13,2 | 14,9 | 17,3 | 18,2 | 19,8 | 20,6 | 12,4 | 9,9 | |||
| 18,5 | 14,8 | 15,7 | 16,7 | 19,4 | 20,4 | 21,3 | 22,2 | 23,1 | 13,9 | 11,1 | |
| 25,4 | 20,3 | 21,6 | 22,9 | 26,7 | 27,9 | 29,2 | 30,5 | 31,8 | 19,1 | 15,3 | |
| 30,8 | 24,6 | 26,2 | 27,7 | 32,3 | 33,9 | 35,4 | 38,5 | 23,1 | 18,5 | ||
| 34,1 | 27,3 | 30,7 | 35,8 | 37,5 | 39,2 | 40,9 | 42,6 | 25,6 | 20,5 | ||
| 35,1 | 28,1 | 29,8 | 31,6 | 36,9 | 38,6 | 40,4 | 42,1 | 43,9 | 26,3 |
5.2 В качестве наглядного примера рассмотрим вариант №1.
5.3 Установление целей и задачи исследования, анализ объекта прогнозирования.
Цель исследования: изучение динамики выпуска продукции и прогнозирование соответствующего показателя на 2004 год.
Задачи исследования:
- построение аппроксимирующих функций, адекватно описывающих исходный динамический ряд;
- выполнение трендового анализа.
- построение прогноза выпуска продукции на 2004 год.
Объектом исследования является выпуск продукции промышленным предприятием.
5.4 Подготовка исходных данных.
Исходные данные представлены в виде динамических рядов за последние семь лет (период 1997 – 2003 г.г.). Динамические ряды представлены в табл. 5.1.
На основе данных табл. 5.1 необходимо создать электронную таблицу в Excel (рис. 5.1).
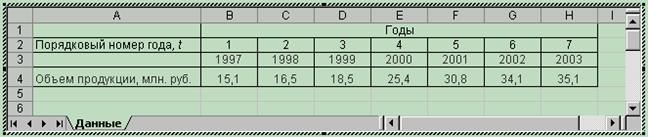
Рис. 5.1 - Вид электронной таблицы с исходными данными
5.5 Фильтрация исходного временного ряда
Фильтрация исходного динамического ряда проводится с использованием процедур сглаживания и выравнивания в автоматическом режиме.
5.6 -Логический отбор видов аппроксимирующих функций
На основании изучения статистических данных табл. 5.1 и логического отбора протекания изучаемого процесса из заданного массива функций отбирают наиболее приемлемые виды уравнений связи. Этот этап необходим, т. к. позволяет при отборе функции учесть основные условия протекания рассматриваемого процесса и требования, предъявляемые к математической модели.
В Excel в качестве аппроксимирующих чаще всего используются следующие функции:
Полиномиальная 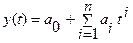 ;
;
Линейная 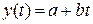 ;
;
Степенная 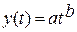 ;
;
Экспоненциальная 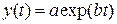 ;
;
Логарифмическая 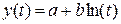 .
.
Для подбора линии тренда необходимо построить график динамики выпуска продукции (рисунок 5.2)
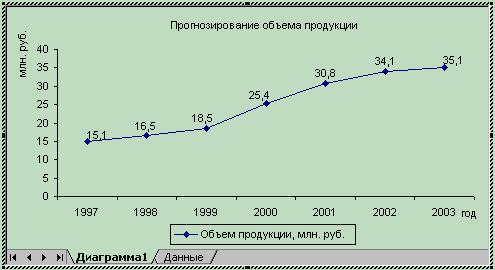
Рис. 5.2 Динамика выпуска продукции
После чего необходимо добавить линию тренда
Когда это возможно, при выборе вида аппроксимирующей функции прибегают к графическому способу подбора по виду точек временного ряда, расположенных на плоскости y0t. Предварительный вывод о качестве подбора линии тренда можно сделать по 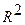 (величина достоверности аппроксимации) – чем ближе значение показателя к единице, тем лучше выполнен подбор уравнения.
(величина достоверности аппроксимации) – чем ближе значение показателя к единице, тем лучше выполнен подбор уравнения.
Результаты подбора двух уравнений тренда представлены на рис. 5.3 и 5.4.
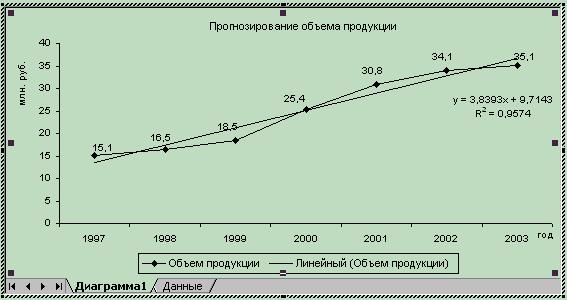
Рис. 5.3 Линейный тренд
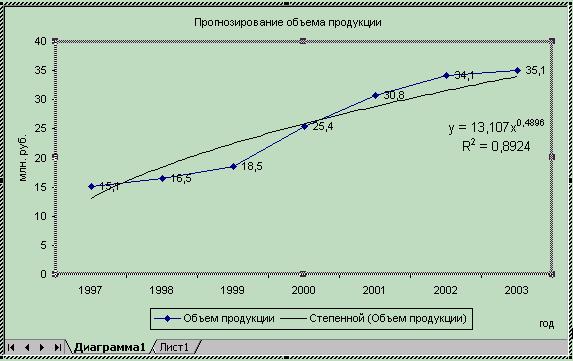
Рис. 5.4 Степенной тренд
Окончательное решение о виде аппроксимирующей функции будет принято после оценки ее качества и точности.
5.7 Оценка параметров математической модели прогнозирования.
На этом этапе исследования определяют параметры различных видов аппроксимирующих функций.
В нашем случае оценка параметров математической модели прогнозирования осуществлялась в автоматическом режиме при построении линии тренда. Результаты определения функций представлены в табл. 5.2.
Таблица 5.2 - Результаты оценки параметров уравнений тренда
| Вид тренда | Уравнение тренда | Величина достоверности аппроксимации |
| Линейная | y = 3,8393x + 9,7143 | R2 = 0,9574; |
| Степенная | y = 13,107*x0,4896 | R2 = 0,8924 |
5.8 Выбор математической модели прогнозирования
Выбор моделей прогнозирования базируется на оценке их качества. Независимо от метода оценки параметров моделей экстраполяции (прогнозирования), их качество определяется на основе исследования свойств остаточной компоненты - Выбор моделей прогнозирования базируется на оценке их качества. Независимо от метода оценки параметров моделей экстраполяции (прогнозирования), их качество определяется на основе исследования свойств остаточной компоненты - 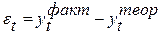 (t = 1, 2, …, n) т.е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчетными значениями.
(t = 1, 2, …, n) т.е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчетными значениями.
Трендовая модель конкретного временного ряда 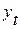 считается адекватной, если остаточная компонента удовлетворяет свойствам случайной компоненты временного ряда:
считается адекватной, если остаточная компонента удовлетворяет свойствам случайной компоненты временного ряда:
1) случайность колебаний уровней остаточной последовательности,
2) соответствие распределения случайной компоненты нормальному закону распределения,
3) равенство математического ожидания случайной компоненты нулю,
4) независимость значений уровней случайной компоненты.
Проведем оценку качества и точности линейного тренда:
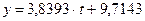
Перед оценкой качества трендовых моделей необходимо рассчитать величину остаточной компоненты. Расчет проводится в следующей последовательности:
5.8.1 рассчитаем теоретические значения каждого уровня динамического ряда. Для этого в таблице с исходными данными (рис. 3.1) в ячейку В6 необходимо ввести формулу для расчета, при этом вместо фактора времени t необходимо указать порядковый номер года (ячейка В2), скопировать полученную формулу в диапазон ячеек С6:I6.
5.8.2 Рассчитать остаточную компоненту временного ряда.
Результаты расчета представлены на рис. 5.5.
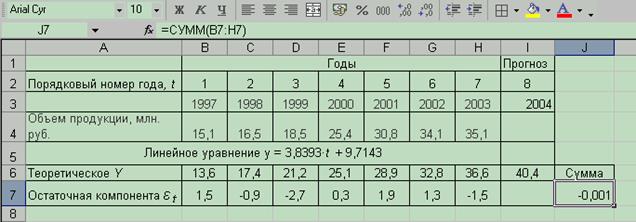
Рис. 5.5 Результаты расчета остаточной компоненты
5.9 Оценка качества трендовой модели включает в себя четыре этапа.
5.9.1Проверка случайности колебаний уровней остаточной последовательности с помощью критерия поворотных точек.
Критерием случайности с доверительной вероятностью 95 %, является выполнение неравенства
К > 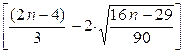 , , | (5.1) |
где К – количество поворотных точек в остаточной последовательности,
Квадратные скобки означают целую часть числа.
Если это неравенство не выполняется, трендовая модель считается неадекватной.
Уровень остаточной последовательности считается поворотной точкой, если он одновременно больше (меньше) двух соседних уровней. В нашем случае К=2, т.к. уровни 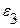 и
и 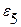 являются поворотными точками (
являются поворотными точками ( 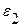 >
> 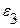 <
< 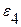 и
и 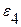 <
< 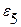 >
> 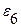 ).
).
2 > 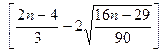 , следовательно
, следовательно 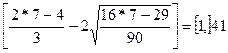 .
.
Так как 2 > 1, то модель считается адекватной.
5.9.2Проверка соответствия распределения случайной компоненты нормальному закону распределения может быть произведена с помощью исследования показателей асимметрии – Ас и эксцесса – Э k :
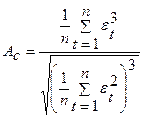 , , | (5.2) |
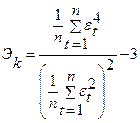 . . | (5.3) |
Если эти коэффициенты близки к нулю или равны нулю, то ряд остатков распределен в соответствии с нормальным законом.
Промежуточные расчеты произведем с помощью электронной таблицы Excel (рис. 5.6).
Воспользовавшись расчетами в таблице, имеем:
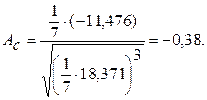
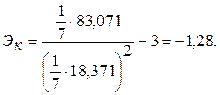
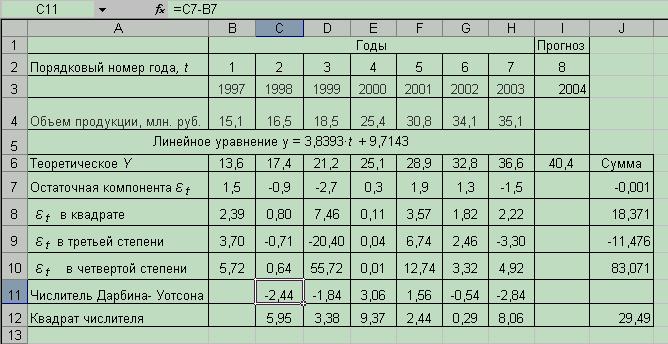
Рис. 5.6 Фрагмент листа «Оценка адекватности модели»
Для оценки близости этих коэффициентов к нулю вычисляют средние квадратические отклонения:
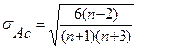 , , | (5.4) |
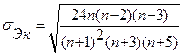 . . | (5.5) |
Средние квадратические отклонения равны:
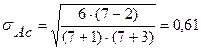 ;
; 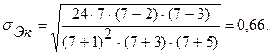
Гипотеза о нормальном характере распределения случайной компоненты принимается, если одновременно выполняются следующие неравенства:
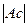 < < 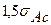 и и 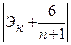 < < 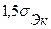 . . | (5.6) |
|-0,38| < 1,5 ·0,61 и 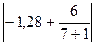 < 1,5 ∙ 0,66.
< 1,5 ∙ 0,66.
Так как оба неравенства выполняются, то гипотеза признается, и модель считается адекватной.
5.9.3проверка равенства математического ожидания случайной компоненты 0, если она распределена по нормальному закону распределения осуществляется на основе t – критерия Стьюдента:
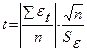 , , | (5.7) |
где 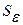 - стандартное (среднеквадратическое) отклонение для этой последовательности.
- стандартное (среднеквадратическое) отклонение для этой последовательности.
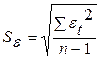 | (5.8) |
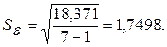
Отсюда 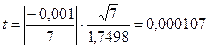
Расчетное значение сравнивается с табличным. Табличное значение критерия Стьюдента имеет степень свободы равную 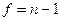 и уровень значимости
и уровень значимости 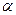 . В данном случае табличное значение критерия равно 2,4469 (при
. В данном случае табличное значение критерия равно 2,4469 (при 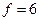 и
и 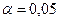 .
.
Так как расчетное значение меньше табличного, модель считается адекватной.
5.9.4Проверка независимости значений уровней остаточной последовательности по критерию Дарбина – Уотсона.
Критерий Дарбина – Уотсона рассчитывается по следующей формуле:
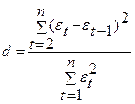 . . | (5.9) |
Подставляя в формулу для расчета данные рис. 3.13, имеем
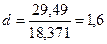
Согласно методу Дарбина – Уотсона существует верхний 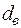 и нижний
и нижний 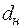 пределы значимости статистики
пределы значимости статистики 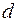 (табл. П.3.3). Эти критические значения зависят от уровня значимости
(табл. П.3.3). Эти критические значения зависят от уровня значимости 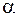 , объема выборки
, объема выборки 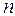 и числа объясняющих переменных
и числа объясняющих переменных 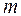 (для трендовых моделей
(для трендовых моделей 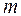 =1).
=1).
Расчетное значение 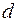 сравнивается с
сравнивается с 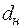 и
и 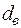 . При этом руководствуются правилами:
. При этом руководствуются правилами:
1. 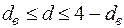 | принимается гипотеза: автокорреляция отсутствует; |
2. 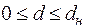 | принимается гипотеза о существовании положительной автокорреляции остатков; |
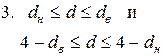 | при выбранном уровне значимости нельзя прийти к определенному выводу; |
4. 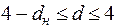 | принимается гипотеза о существовании отрицательной автокорреляции остатков. |
Табличные значения критерия Дарбина – Уотсона для временного ряда, содержащего 7 уровней равны 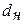 = 0,7 и
= 0,7 и 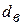 = 1,36.
= 1,36.
В нашем случае расчетное значение критерия попало в следующий промежуток: 1,36 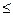 1,6
1,6 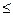 4 – 1,36, следовательно, принимается гипотеза об отсутствии автокорреляции. Модель признается адекватной.
4 – 1,36, следовательно, принимается гипотеза об отсутствии автокорреляции. Модель признается адекватной.
5.9.5оценка точности модели с помощью ошибки аппроксимации
Ошибка аппроксимации рассчитывается по следующей формуле:
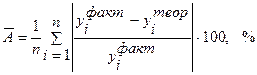 | (5.10) |
Последовательность расчета ошибки аппроксимации аналогична расчету ошибки аппроксимации в многофакторной корреляционно-регрессионной модели. Результаты расчетов представлены на рис. 5.7
В нашем случае ошибка аппроксимации равна 6,58%. Так как ошибка аппроксимации меньше критических значений (8-10%), то выбранное уравнение тренда достаточно точно описывает исходную информацию.
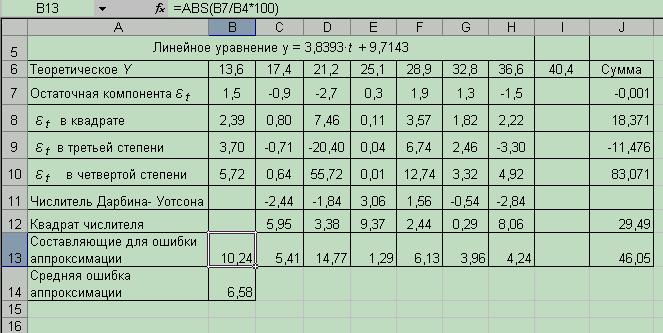
Рис. 5.7 Расчет ошибки аппроксимации
Проведенный анализ показал, что линейный тренд адекватно и точно описывает исходный динамический ряд и его можно использовать для прогнозирования.
5.10 Проведем оценку качества и точности степенного тренда:
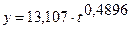
Проверка осуществляется аналогично. Результаты промежуточных расчетов представлены на рис. 5.8.
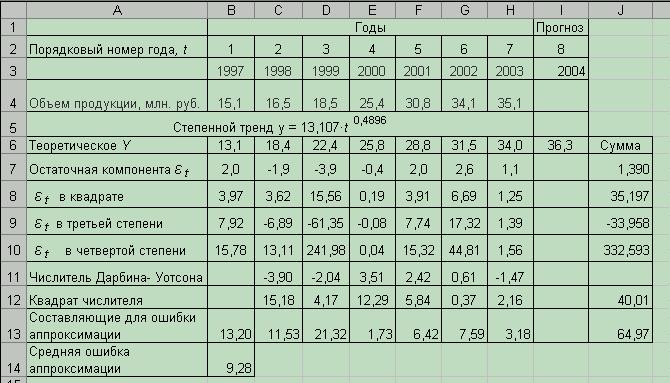
Рис. 5.8 Фрагмент листа «Оценка адекватности степенного тренда»
5.10.1 Проверка случайности колебаний уровней остаточной последовательности с помощью критерия поворотных точек
В нашем случае количество поворотных точек К=2, так как 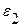 >
> 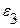 <
< 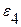 и
и 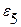 <
< 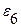 >
> 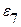 ).
).
Так как 2 > 1, то модель считается адекватной.
5.10.2 Проверка соответствия распределения случайной компоненты нормальному закону распределения
Коэффициент асимметрии равен:
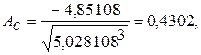
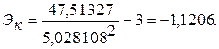
Средние квадратические отклонения равны:
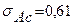 ;
; 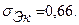
Гипотеза о нормальном характере распределения случайной компоненты принимается, если одновременно выполняются следующие неравенства:
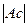 <
< 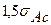 и
и 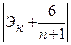 <
< 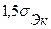 .
.
|-0,43| < 1,5 · 0,61 и 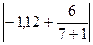 < 1,5 ∙ 0,66.
< 1,5 ∙ 0,66.
|-0,43| < 0,915 и 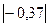 < 0,99
< 0,99
Так как оба неравенства выполняются, гипотеза о нормальном характере распределения случайной компоненты признается, и модель считается адекватной.
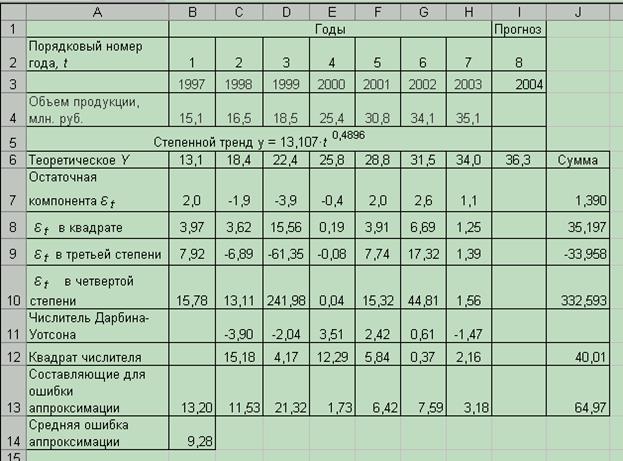
Рис. 5.9 Фрагмент листа «Оценка адекватности степенного тренда»
5.10.3 Проверка равенства математического ожидания случайной компоненты нулю, если она распределена по нормальному закону распределения.
Расчетное значение критерия Стьюдента равно:
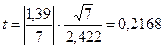
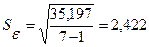
Расчетное значение сравнивается с табличным. Табличное значение критерия Стьюдента имеет степень свободы равную 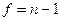 и уровень значимости
и уровень значимости 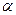 . В данном случае табличное значение критерия равно 2,4469 (при
. В данном случае табличное значение критерия равно 2,4469 (при 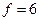 и
и 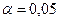 ). Так как расчетное значение меньше табличного, модель считается адекватной.
). Так как расчетное значение меньше табличного, модель считается адекватной.
5.10.4 Проверка независимости значений уровней остаточной последовательности по критерию Дарбина – Уотсона
Критерий Дарбина – Уотсона равен:
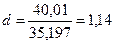 .
.
Табличные значения критерия Дарбина – Уотсона для временного ряда, содержащего 7 уровней равны 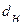 = 0,7 и
= 0,7 и 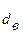 = 1,36 (табл. П.3.3 [1]).
= 1,36 (табл. П.3.3 [1]).
В данном случае расчетное значение критерия Дарбина – Уотсона попало в третий интервал, когда 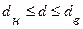 , т.е.
, т.е. 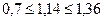 . В этой ситуации нельзя прийти к определенному уровню.
. В этой ситуации нельзя прийти к определенному уровню.
Следовательно, необходимо рассчитать коэффициент автокорреляции по формуле:
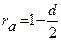 | (5.11) |
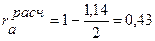
Расчетное значение сравнивается с табличным 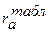 (табл. П.3.4 [1]). Табличное значение коэффициента автокорреляции имеет одну степень свободы f = n = 7. Так как расчетное значение больше табличного (
(табл. П.3.4 [1]). Табличное значение коэффициента автокорреляции имеет одну степень свободы f = n = 7. Так как расчетное значение больше табличного ( 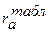 = 0,370), то гипотеза об отсутствии автокорреляции в остаточной последовательности отвергается и модель признается неадекватной.
= 0,370), то гипотеза об отсутствии автокорреляции в остаточной последовательности отвергается и модель признается неадекватной.
5.10.5 Оценка точности модели с помощью ошибки аппроксимации
Воспользовавшись расчетами в таблице (рис. 5.9), находим, что ошибка аппроксимации равна 9,28 %.
Проведенный анализ показал, степенную модель нельзя использовать для дальнейшего прогнозирования, так как в исходных данных присутствует автокорреляция уровней и значение средней ошибки аппроксимации достаточно близко к критическому значению (8-10%).
Следовательно, для прогнозирования необходимо оставить линейное уравнение тренда.
5.11 Получение точечного прогноза.
Сделаем прогноз на последующий 2004 год, используя при этом выбранную нами адекватную модель – линейную функцию.
Для этого в уравнение 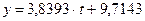 подставить прогнозное значение t, которое в нашем случае равно 8.
подставить прогнозное значение t, которое в нашем случае равно 8.
Итак, 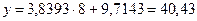 , млн. руб.
, млн. руб.
Следовательно, в следующем году, при сложившихся тенденциях работы промышленного предприятия, объем выпуска продукции составит 40,43 млн. руб.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Цели и задачи исследования, анализ объекта прогнозирования.
6.2 Логический отбор видов аппроксимирующей функции.
6.3 Оценка параметров математической модели прогнозирования.
6.4 Выбор математической модели прогнозирования.
6.5 Точечный прогноза.
6.6 Выводы.
Контрольные вопросы и защита работы
7.1 Дать определение временного ряда.
7.2 Дать определение тренда.
7.3 Компоненты временного ряда.
7.4 Этапы прогнозирования при помощи методов экстраполяции.
7.5 Наиболее распространенные функции для построения тренда.
7.6 Что такое остаточная компонента.
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы представленных выше.
Практическое занятие 26.
Метод скользящего среднего
Цель и содержание
Цель работы – приобрести навыки прогнозирования по методу скользящего среднего.
В результате выполнения работы студенты должны:
1. Изучить теоретические основы метода.
2. Произвести выравнивание ряда.
3. Найти прогнозируемое значение.
4. Произвести оценку качества и точности модели.
5. Сделать выводы.
Теоретическое обоснование
При использовании этой методики основное положение состоит в том, что временной ряд является устойчивым в том смысле, что его члены 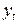 являются реализациями следующего случайного процесса:
являются реализациями следующего случайного процесса:
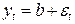 , , | (2.1) |
где 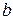 – неизвестный постоянный параметр, который оценивается на основе представленной информации,
– неизвестный постоянный параметр, который оценивается на основе представленной информации,
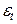 – случайный компонент (или шум) в момент времени t. Предполагается, что случайная ошибка
– случайный компонент (или шум) в момент времени t. Предполагается, что случайная ошибка 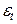 имеет нулевое математическое ожидание и постоянную дисперсию. Кроме того, предполагается, что данные для различных периодов времени не коррелированны.
имеет нулевое математическое ожидание и постоянную дисперсию. Кроме того, предполагается, что данные для различных периодов времени не коррелированны.
Метод с использованием скользящего среднего предполагает, что последние n наблюдений являются равнозначно важными для оценки параметра b. Другими словами, если в текущий момент времени t последними n наблюдениями есть 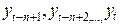 , тогда оцениваемое значение для момента t+1 вычисляется по формуле:
, тогда оцениваемое значение для момента t+1 вычисляется по формуле:
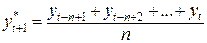 . . | (2.2) |
Не существует четкого правила для выбора числа n – базы метода, использующего скользящее среднее. Если есть весомые основания предполагать, что наблюдения в течение достаточно длительного периода времени удовлетворяют модели 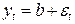 , то рекомендуется выбирать большие значения n. Если же необходимые значения удовлетворяют приведенной модели в течение коротких периодов времени, может быть приемлемым и малое значение n. На практике величина n обычно принимается в пределах от 2 до 10.
, то рекомендуется выбирать большие значения n. Если же необходимые значения удовлетворяют приведенной модели в течение коротких периодов времени, может быть приемлемым и малое значение n. На практике величина n обычно принимается в пределах от 2 до 10.
Чтобы проверить применимость метода скользящего среднего проанализируем данные таблицы 2.1
Таблица 2.1 – Исходные данные
| Месяц, t | Спрос, yt | Месяц, t | Спрос, yt |
Данные показывают, что наблюдается возрастание значений yt с течением времени. Это, вообще-то означает, что скользящее среднее не будет хорошим предсказателем для будущего спроса. В частности, использование большой базы n для скользящего среднего не приемлемо в этом случае, так как это приведет к подавлению наблюдаемой тенденции в изменении данных. Следовательно, если мы используем небольшое значение для базы n, то будем находиться в лучшем положении с точки зрения отображения упомянутой тенденции в изменении данных.
Если мы используем значение n=3 в качестве базы скользящего среднего, то оценка спроса на следующий месяц ( t=25) будет равна средней величине спроса за 22, 23 и 24 месяцы:
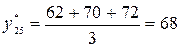 единиц.
единиц.
Оценка величины спроса в 68 единиц для 25 месяца будет использоваться также при прогнозе спроса для t=26:
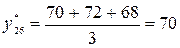 единиц.
единиц.
Когда значение реального спроса в 25 месяце будет известно, его следует использовать для вычисления новой оценки объема спроса для 26 месяца в виде средней величины спроса 23, 24 и 25 месяцев.
Средство вычисления скользящего среднего является составной частью надстройки Пакет анализа Excel. Для его использования выполните команду Сервис  Анализ данных
Анализ данных  Скользящее среднее. В открывшемся одноименном диалоговом окне укажите местоположение на рабочем листе исходных данных (в поле ввода Входной интервал). Для вывода графика установите флажок Вывод графика. На рисунке 2.1 показано заполненное окно Скользящее среднее, результаты работы этого средства представлены на рисунке 2.2.
Скользящее среднее. В открывшемся одноименном диалоговом окне укажите местоположение на рабочем листе исходных данных (в поле ввода Входной интервал). Для вывода графика установите флажок Вывод графика. На рисунке 2.1 показано заполненное окно Скользящее среднее, результаты работы этого средства представлены на рисунке 2.2.
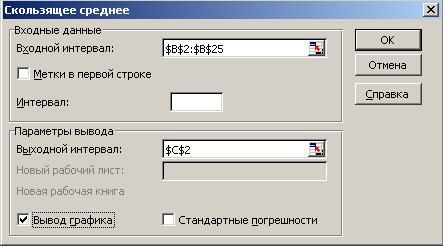
Рисунок 2.1 – Пример заполнения диалогового окна Скользящего среднего
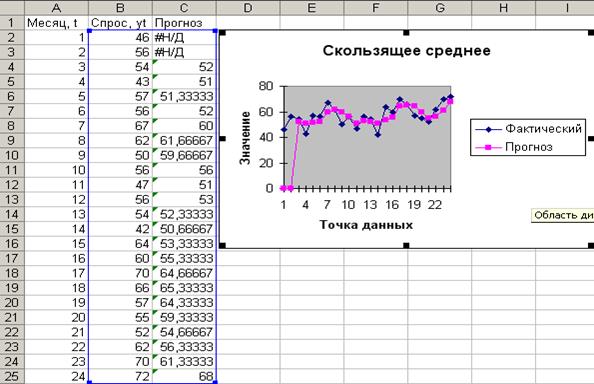
Рисунок 2.2 – Результаты расчетов.
Оценка качества и точности модели производится аналогично оценке, проведенной влаботаторной работе 1.
Аппаратура и материалы
Микрокалькулятор, программное обеспечение MS Excel.
