Комплексный чертеж цилиндрической винтовой линии
Из пространственных кривых наибольшее распространение находят винтовые линии. Цилиндрической винтовой линией называется множество последовательных положений точ-ки, совершающей равномерное перемещение по прямой, которая равномерно вращается вокруг параллельной ей оси.
За один оборот прямой вокруг оси точка переместится по прямой на величину P, называемую шагом винтовой линии. Так как рассматриваемые движения точки равномерны и взаимосвязаны, то, например, повороту точки на угол 180° (половина оборота) будет соот-ветствовать перемещение по прямой на половину шага. По аналогии, за 1/n часть оборота точка перемещается на 1/n шага. На этом основывается построение комплексного чертежа цилиндрической винтовой линии.
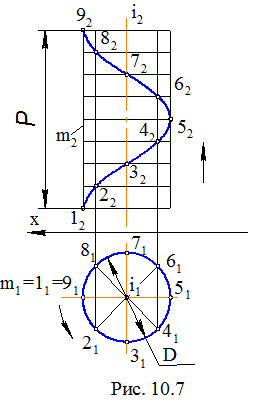
Пусть ось винтовой линии i перпендику-лярна П1, начальное положение прямой m, параллельной оси i, и точки задано проекциями m1, m2 и 11, 12 соответственно (рис. 10.7). Проекцией винтовой линии на П1 будет окружность, так как расстояние от точки до оси i не изменяется и равно D/2. Для построения фронтальной проекции винтовой линии разделим окружность на П1 и отрезок на П2, соответствующий шагу P, на равное количество частей (на рис. 10.7 – 8 частей). Тогда повороту прямой m на 1/8 часть оборота будет соответствовать линейное перемещение точки на 1/8 шага. На рис. 10.7 точка занимает положение 2(21, 22). При повороте прямой еще на 1/8 часть оборота, точка поднимется еще на 1/8 часть шага – точка 3(31, 32) и т. д. Полученные фронтальные проекции точек винтовой линии соединяем по лекалу.
Если вращение прямой вокруг оси выполняется против часовой стрелки, и точка при этом поднимается вверх, то такая винтовая линия называется правой винтовой линией. Если вращение выполняется по часовой стрелке, и точка при этом поднимается вверх, то винтовая линия называется левой винтовой линией. Прямая m при вращении вокруг оси i описывает цилиндрическую поверхность вращения, поэтому винтовая линия называется цилиндрической винтовой линией. Все точки этой винтовой линии принадлежат цилиндрической поверхности вращений.
Обратим внимание на то, что горизонтальной проекцией цилиндрической винтовой линии является окружность, а фронтальной – кривая, которая называется синусоидой. Для получения более точного чертежа винтовой линии необходимо окружность делить на большее число частей (n >8).
Если при тех же условиях образования винтовой линии прямая m пересекает ось i, то такая винтовая линия называется конической винтовой линией.
ПОВЕРХНОСТИ
Понятие поверхности
В начертательной геометрии поверхности рассматриваются как множество последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхности называется кинематическим.
Линия (кривая или прямая) движется в пространстве по определенному закону и создает поверхность. Она называется образующей. В процессе образования поверхности она может оставаться неизменной или менять свою форму. Закон перемещения образующей задается в виде совокупности линий и указаний о характере перемещения образующей. Эти линии называются направляющими.
Кроме кинематического способа, поверхность может быть задана
· аналитически, т. е. описана математическим выражением;
· каркасным способом, который используется при задании сложных поверхностей; каркас поверхности представляет собой упорядоченное множество точек или линий, принадлежащих поверхности.
Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов называется определителем поверхности.
Определитель поверхности состоит из двух частей:
· геометрической части, включающей постоянные геометрические элементы (точки, линии), которые участвуют в образовании поверхности;
· алгоритмической части, задающей закон движения образующей, характер изменения ее формы.
В символическом виде определитель поверхности F можно записать в виде: F(Г)[A], где Г – геометрическая часть определителя, А – алгоритмическая.
Чтобы у поверхности выделить определитель, следует исходить из кинематического способа ее образования. Но так как многие одинаковые поверхности могут быть получены различными путями, то они будут иметь различные определители. Ниже будут рассмотрены наиболее распространенные поверхности в соответствии с классификационными признаками, приятыми в курсе начертательной геометрии.
