Угол между плоскостями

Для двух плоскостей существует понятие двугранного угла.

Определение. Двугранным углом называется фигура, образованная прямой t и двумя полуплоскостями с общей границей t , не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями, прямая t – ребром двугранного угла. Двугранный угол с гранями Σ и Δ и ребром t обозначается ΣtΔ.

Отметим на ребре точку и в каждой грани из этой точки проведем луч перпендикулярно ребру. Образованный этими лучами угол называется линейным углом двугранного угла. Линейный угол служит мерой двугранного угла. Величина двугранного угла не зависит от выбора его линейного угла.

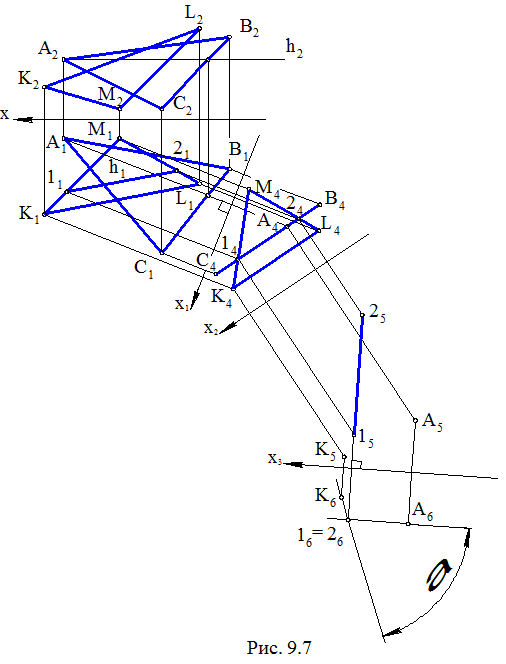
Задача. Даны две плоскости Σ(ΔАВС) и Δ(ΔKML). Определить угол между плоскостями (рис. 9.7).

Проекционное решение задачи заключается в построении линии пересечения плоскостей Σ и Δ, являющейся по определению ребром двугранного угла, и последующим проецированием ее в точку на дополнительной плоскости проекций. Исходные плоскости Σ и Δ будут иметь на этой плоскости вырожденные проекции – прямые, пересекающиеся в указанной точке. Угол между этими прямыми есть решение задачи. Последовательность предлагаемого проекционного решения будет следующей:

1) в одной из двух данных плоскостей, например Σ, строится линия уровня, например h(h₁, h₂ ), где h₂ // х;

2) введением новой системы плоскостей проекций П₁ , П₄ с осью x₁ ^ h₁ и П₄ ^ h

строятся на П₄ дополнительные проекции плоскостей – В₄С₄ для Σ и ΔK₄M₄L₄ для

плоскости Δ;

3) отмечаются отрезки 1₄2₄ и 1₁2₁ – дополнительные проекции линии t(1₁2₁,1₄2₄₎)

пересечения заданных плоскостей;

4) в каждой из плоскостей Σ и Δ выбирается по одной точке, например А Î Σ и

К Î Σ;

5) введением новой системы плоскостей проекций П₄ , П₅ с осью x₂ // 1₄2₄ и

П₅ // t(1,2) строятся на П₅ дополнительные проекции 1₅2₅, А₅, К₅ соответствующих фигур: линии пересечения t (1, 2) и точек А, К;

6) введением новой системы плоскостей проекций П₅ , П₆ с осью x₃ ^ 1₅2₅ и

П₆ ^ t(1,2) строится на П₆ линейный угол a двугранного угла ΣtΔ, который и

является решением задачи.

Возможно другое проекционное решение рассматриваемой задачи, основанное на следующем алгоритме:

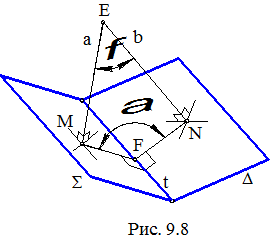
1) в пространстве выбирается произвольная

точка Е (рис. 9.8)

2) опускаются два перпендикуляра : а ^ Σ, где а проходит через точку Е; b ^ Δ, где b проходит также через точку Е;

3) из свойств плоского четырехугольника EMFN следует, что величина a искомого линейного угла двугранного угла ΣtΔ равна 180°– j, где j = Ð(a, b).

Задача. Даны плоскости Σ(АВ, DC), где АВ Ç DC и Δ(KL, PT), где KL // PT

(рис. 9.9). Требуется построениями определить угол между плоскостями.

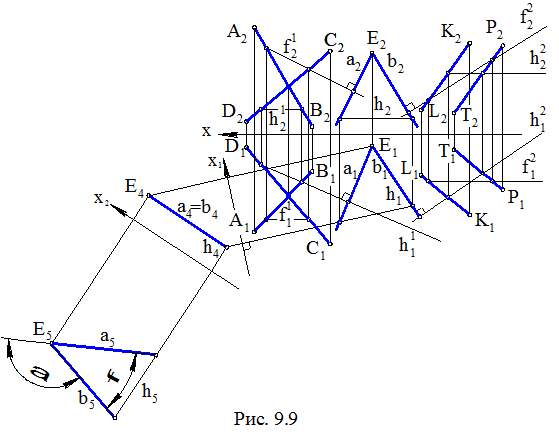
Последовательность проекционного решения может быть следующей:

1) в плоскости Σ строятся линии уровня f(f₁¹, f₂¹ ) и h(h₁¹, h₂¹ ), где f₁¹ // х, h₂¹ // х, а в плоскости Δ – линии уровня h²(h₁² , h₂² ) и f²(f₁² , f₂² ), где h₂² // х, f₁² // х;

2) из точки Е пространства опускаются два перпендикуляра – а (а₁,а₂ ) ^ Σ и

b (b₁, b₂ ) ^ Δ, при этом а₂ ^ f₂¹ , b₂ ^ f₂² , a₁ ^ h₁¹ , b₁ ^ h₁² ;

3) в плоскости построенных пересекающихся прямых а и b выбирается линия

уровня, например h(h₁, h₂ ), где h₂ // х;

4) вводится новая система плоскостей проекций П₁, П₄ с осью x₁ ^ h₁ и П₄ ^ h ;

5) на П₄ строится вырожденная проекция а₄ = b₄ плоскости прямых а и b;

6) вводится новая система плоскостей проекций П₄ , П₅ с осью x₂ // а₄ и П₅ // (а,b), где (а, b) – плоскость прямых а и b;

7) на П₅ строится угол j = Ð( а₅ , b₅ ), который позволяет определить искомый угол a между плоскостями Σ и Δ, равный 180° – j.

В соответствии с понятием угла в стереометрии, угол между плоскостями должен быть острым. Поэтому необходимо принять в приведенном проекционном решении значение угла между плоскостями Σ и Δ, равное φ.

КРИВЫЕ ЛИНИИ

Кривая линия – это множество последовательных положений точки, перемещающейся в пространстве. Такое определение дает наглядное представление о кривой линии как о траектории точки.

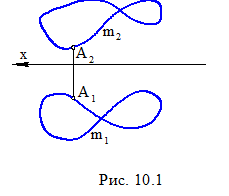
Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить между собой одноименные проекции в той же последовательности, в какой они располагались на ней в пространстве. При задании кривой ее проекциями необходимо указать проекции хотя бы одной точки, принадлежащей кривой. Так, если на проекциях кривой m (рис. 10.1) не указать проекции точки A (A₁, A₂), то только по проекциям m₁ и m₂ нельзя судить о форме кривой.

Линии подразделяются на алгебраические, если в декартовой системе координат они определяются алгебраическими уравнениями, и трансцендентные, если они описываются трансцендентными уравне-ниями.

К алгебраическим линиям, в частности, отно-сятся окружность, эллипс, парабола, гипербола, астроида и другие.

К трансцендентным линиям относятся сину-соида, спираль Архимеда, циклоида и другие.

Линии могут быть пространственными и плоскими.

Линии, у которых все точки принадлежат одной плоскости, называют плоскими.

Кривая, точки которой не лежат в одной плоскости, называется пространственной кривой. Примером плоской кривой является окружность, примером пространственной кривой – цилиндрическая винтовая линия.

10.1. Свойства кривых, инвариантные относительно ортогонального проецирования

При построении ортогональных проекций кривых необходимо знать те их свойства, которые сохраняются (инвариантны) при проецировании. К таким свойствам относятся следующие:

1. Касательные к кривой проецируются в касательные к ее проекциям (за исключением, когда касательная проецируется в точку).

2. Несобственным (бесконечно удаленным) точкам кривой соответствуют несобственные точки ее проекции.

При проецировании плоских кривых в дополнение к отмеченным будут справедливы следующие свойства:

3. Порядок проекции алгебраической кривой равен порядку самой кривой. Порядок алгебраической кривой определяется степенью уравнения, описывающего эту кривую.

4. Число узловых точек (точек, в которых кривая пересекает саму себя) на проекции кривой равно числу узловых точек самой кривой.