Техника вычисления пределов
Подставить значение, к которому стремиться х в функцию. Если предел вычисляется, то полученное значение и будет пределом данной функции.
Чему равен предел: Lim 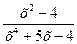
х→1
Если предел не вычисляется, то надо применить определенную технику
Могут возникнуть неопределенности: ∞/∞; 0/∞; 0/0 и т.д.
1. Деления на максимальную степень.
Чему равен предел: Lim 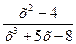
х→ ∞
2. Разложение квадратного трехчлена на множители
Чему равен предел: Lim 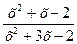
х→ -2
Левый и правый предел функции
Опр. Если число А1 есть предел функции при х→а, так, что х принимает только значения > a, то число А1 называется правым пределом функции.
lim f(x)= А1
х→а+0
аналогично:
Опр. Если число А2 есть предел функции при х→а, так, что х принимает только значения < a, то число А2 называется левым пределом функции.
lim f(x)= А2 Если А1 = А2= А, то это предел функции
х→а-0
Примеры :В. А. Подольский № 7.46,7.47;7.48;7.51
Пр. Найти придел функции у = 1/(х+2)
lim 1/(х+2) = - ∞
х→-2-0
lim 1/(х+2) = + ∞
х→-2+0
Найти придел функции у = х/(х-3)
lim х/(х-3) = + ∞ lim х/(х-3) = - ∞
х→-3-0 х→-3+0
Непрерывность и точки разрыва
1. Приращение аргумента и приращение функции
Если х1 и х2 –значения аргумента х, а f(x1) и f(x2) значения функции y=f(x), то ∆х= x2 – x1, называется приращением аргумента на отрезке [x2 , x1], а величина ∆у= f(x2) - f(x1)=f(x+∆х) –f(x) , ∆у – приращение функции на этом отрезке.
Пример:
Вычислить приращение аргумента и приращение функции у=х2-2х+3
а) от х1=0 до х2=1;
б) от х1=-1 до х2=3;
а) ∆х= x2 – x1 =1- 0 = 1; ∆у = 1-2+3-3= -1
б) ∆х= x2 – x1 = 3-(-1) = 4; ∆у = 9-6+3-(1+2+3) = 0
пр. 7.175; 7.178-7.180
Первое определение непрерывности
Функция y=f(x) называется непрерывной в (.) х= а, если бесконечно малому приращению аргумента в этой точке, соответствует бесконечно малое приращение функции.
lim ∆у = 0
∆х→а
Второе определение непрерывности
Функция y=f(x) называется непрерывной в (.) х= а, если:
- она определена в (.) х= а, т.е существует ее значение в (.) х= а, равное f(а);
- существует конечный предел функции в этой точке, т.е. lim f(x)= А;
х→а
- этот предел равен значению функции в (.) х= а, т.е. . lim f(x)= А= f(а).
х→а
Примером непрерывности функции может служить любая элементарная функция. Которая непрерывна в каждой точке своей области определения.
Точка х=а называется точкой разрыва функции y=f(x), если эта функция определена в некоторой окрестности точки х= а, но в самой точке х= а не удовлетворяет условию непрерывности.
Точки разрыва функции делятся на два типа. К точкам разрыва первого рода относятся такие точки, в которых существуют конечные односторонние пределы (левый и правый предел).
К точкам разрыва второго рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
Точки разрыва первого рода делятся в свою очередь на точки. В которых разрыв устраним, когда lim f(x)= lim f(x) ≠ f(а) х→а-0 х→а+0
И на точки скачка функции, когда lim f(x)= lim f(x) ≠ f(а)
х→а-0 х→а+0
а разность f(а+0) - f(а+0) называется скачком функции в точке х= а.
Пр.Исследовать функцию на разрыв у = 1/(х+3)
ООФ функция определена при х? ( -∞;-3 ) (-3; +∞)
Найдем левый и правый пределы
lim 1/(х+3) = - ∞
х→-3-0
lim 1/(х+3) = + ∞
х→-3+0
Данная функция имеет разрыв второго рода в точке х=-3, т.к. левый и правый пределы бесконечны.
Рис.
Пр. Исследовать функцию на разрыв у =1/(1+21/х)
ООФ х ≠ 0
lim 1/(1+21/х) = 1
х→-- 0
lim 1/(1+21/х) = 0
х→-+ 0
Данная функция имеет разрыв первого рода в точке х=0, так-так левый и правый придел имеют конечные значения. Имеется скачек функции.
Рис.
Пр.Исследовать функцию на разрыв у = 1/(х+5)2
ООФ функция определена при х? ( -∞;-5 ) (-5; +∞)
Найдем левый и правый пределы
lim 1/(х+5)2 = + ∞
х→-5-0
lim 1/(х+5)2 = + ∞
х→-5+0
Данная функция имеет разрыв второго рода в точке х = -5, т.к. левый и правый пределы бесконечны.
Рис.
 Пр. Исследовать функцию на разрыв
Пр. Исследовать функцию на разрыв
х при х ≤ 0
х2 при 0 < х ≤ 1
x +1 при х >1
Найдем левые и правые приделы в точках изменения функции:
lim х2= 1 lim х+1= 2 lim х2= 0 lim х = 0
х→1—0 х→1+ 0 х→+ 0 х→- 0
Функция имеет разрыв 1-го рода со скачком функции в точке х =1
Рис.
Пр . Исследовать функцию на разрыв у =31/х
ООФ х ≠ 1
Найдем левые и правые приделы
lim 31/х = 0
х→- 0
lim 31/х = +∞
х→+0
Данная функция имеет разрыв второго рода в точке х = 0, т.к. правый предел бесконечен.
