Общие сведения об уравнениях и их решении

Решение многих научных и технических задач сводится к составлению и решению уравнений. Следовательно, специалист в любой отрасли техники должен уметь решать любые уравнения как обычными средствами вычислений, так и с помощью компьютера.

Обычно уравнения имеют вид f (x)=0, где f-заданная функция.

Уравнения называются нелинейными , если линия , построенная по заданной функции, не является прямой. Нелинейные уравнения делятся на два класса : алгебраические и трансцендентные. Алгебраическими называют уравнения, если заданная функция является полиномом n - ой степени . Нелинейные уравнения, содержащие тригонометрические, логарифмические и другие элементарные функции называются трансцендентными .

Поиски методов решения нелинейных уравнений начались с попыток вывода формул, аналогичных формуле для решения квадратного уравнения , которая выражает значения корней уравнения через его коэффициенты . Для алгебраических уравнений третьей и четвертой степени такие формулы были получены. Однако практическое значение этих формул невелико, так как их применение приводит к дополнительным и довольно сложным вычислениям. Покажем это на примере решения кубического уравнения .

Пусть дано кубическое уравнение у ³ + а у ² + в у + с = 0. Заменяя в уравнении неизвестное у новым неизвестным x, связанным с у равенством у= x- а /3, получают уравнение относительно неизвестного x, не содержащее квадрата этого неизвестного, т.е. уравнение вида:

x + p x + q = 0 (1) .

Если будут найдены корни уравнения ( 1 ) ,то можно получить и корни заданного уравнения благодаря равенству у = x - а / 3 . Следовательно, необходимо уметь решать « неполное» кубичное уравнение . Формулы, выражающие корни уравнения (1) через его коэффициенты при помощи квадратных и кубичных радикалов , были получены итальянским математиком Кардано в ХV I веке . Формулы Кардано имеют следующий вид :

X= 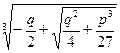+ 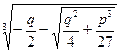(2)

Так как кубичный радикал имеет в поле комплексных чисел три значения, то формула (2) дает по три значения для каждого радикала, входящего в формулу (2). Однако, применяя формулу Кардано, нельзя комбинировать любое значение первого радикала с любым значением второго. Для данного значения первого радикала a следует брать лишь то из значений второго радикала b , которое удовлетворяет условию a b = - p /3 .

В курсе высшей алгебры доказано, что при определенных соотношениях коэффициентов p и q в уравнении (1), все три корня этого уравнения являются действительными числами. Однако разыскание их по формуле Кардано требует извлечения кубичных корней из комплексных чисел, что возможно сделать лишь путем перехода к тригонометрической форме этих чисел. Поэтому запись корней кубичного уравнения с помощью радикалов не имеет практического значения .

Аналогично обстоит дело и с решением алгебраических уравнений четвертой степени. Формулы, выражающие корни уравнения через его коэффициенты, были получены итальянским математиком Феррари еще в ХVI столетии, однако в практических расчетах никто ими не пользуется в связи с их громозкостью и сложностью вычислений.

После Феррари почти три столетия продолжались безуспешные попытки сделать следующий шаг, т.е. найти формулы, выражающие корни уравнения пятой степени через его коэффициенты. Эти попытки прекратились лишь после того, как норвежский математик Абель в двадцатых годах XIX столетия доказал, что такие формулы для уравнений n - ой степени при любом n ³5 заведомо не могут быть найдены.

Это обстоятельство послужило толчком для многочисленных исследований, имевших целью получение методов приближенного вычисления корней. Такой подход оправдан еще и тем, что при решении технических проблем обычно достаточно знать лишь приближенные значения корней с заранее заданной точностью. Если бы корни многочлена и можно было бы записать в радикалах, то эти радикалы все равно были бы заменены их приближенными значениями. Кроме того, уравнение может содержать коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнений теряет смысл. Все указанные причины привели к появлению так называемых итера-ционных методов решения нелинейных уравнений. С их помощью решение уравнения достигается путем многократного применения некоторого алгоритма, который позволяет вычислить приближенные значения корней уравнения с заранее заданной точностью. Обычно это делается в два этапа:

1). о т д е л е н и е к о р н е й, т.е. установление возможно тесных промежутков [a ,b] , в которых содержится один корень уравнения ;

2). у т о ч н е н и е п р и б л и ж е н н ы х к о р н е й , т.е. доведение их до заданной степени точности.

Д а л е е р а с с м о т р е н к а ж д ы й и з э т а п о в .