Матрица линейного преобразования

Линейная зависимость векторов.

Выражение вида λ 1* A 1+ λ 2* A 2+...+ λn * An называется линейной комбинацией векторов A 1, A 2,..., An с коэффициентами λ 1, λ 2,..., λn .

Определение линейной зависимости системы векторов

Система векторов A 1, A 2,..., An называется линейно зависимой, если существует ненулевой набор чисел λ 1, λ 2,..., λn , при котором линейная комбинация векторов λ 1* A 1+ λ 2* A 2+...+ λn * An равна нулевому вектору, то есть система уравнений: A 1 x 1+ A 2 x 2+...+ Anxn = Θ имеет ненулевое решение.

Набор чисел λ 1, λ 2,..., λn является ненулевым, если хотя бы одно из чисел λ 1, λ 2,..., λn отлично от нуля.

Базис векторного пространства.

Базисом системы векторов A 1 , A 2 ,..., An называется такая подсистема B 1, B 2 ,..., Br (каждый из векторов B 1, B 2,..., Br является одним из векторов A 1 , A 2 ,..., An ), которая удовлетворяет следующим условиям:

1. B 1 , B 2 ,..., Br линейно независимая система векторов;

2. любой вектор Aj системы A 1 , A 2 ,..., An линейно выражается через векторы B 1, B 2,..., Br

r - число векторов входящих в базис.

Теорема 29.1 О единичном базисе системы векторов.

Если система m -мерных векторов содержит m различных единичных векторов E 1 E 2 ,..., Em , то они образуют базис системы.

Разложение вектора по базису.

Разложить вектор X по базису e 1 , e 2 , e 3 - значит, представить вектор

X в виде : X = α 1 e 1 + α 2 e 2 + α 3 e 3; где e 1 = ( x 1 , y 1, z 1), e 2 = ( x 2 , y 2 , z 2 ),

e3 = ( x3 , y3 , z3 ),

x = ( x , y , z )

Замена базиса векторного пространства.

процедура замены базиса и преобразования координат (т.е. процедура перехода от одного пространства к другому). Транспонированная матрица А* составленная из коэффициентов называется матрицей замены базиса на базис ( ). Сама же матрица А, составленная из коэффициентов является матрицей замены базиса на базис ( ).

Евклидово пространство.

Линейное пространство наз евкл, если в нем определена операция скалярного произведения,т е двум люб векторам х и у, сопоставлено вещественное число, обозначаемое (х.у) и это соотв удовл след усл

( x , y) = (y, x),

( α· x , y) = α·(x, y),

(x + y, z) =(x, z) + (y, z),

( x , x)> 0 при x ≠ 0, (0, 0) = 0,

то в пространстве L определено скалярное произведение ( x , y ).

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

Ортонормированный и ортогональный базисы.

Ортонормированная система, состоящая из n векторов n -мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.

Если e 1, e 2, ..., en — ортонормированный базис n -мерного евклидова пространства и x = x 1 e 1 + x 2 e 2 + ... + xnen — разложение вектора x по этому базису, то координаты xi вектора x в ортонормированном базисе вычисляются по формулам xi =( x , ei ), i = 1, 2, ..., n . Базис e1, e2, … , en в n –мерном евклидовом пространстве En называется ортогональным, если ( ei , ej ) = 0 " i ≠ j , т.е. все векторы попарно ортогональны.

Ортогональный базис из единичных векторов называется ортонормированным.

Линейные преобразования и их свойства.

Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y , причём:

x + y = y + x − сложение коммутативно;

x + ( y + z ) = ( x + y ) + z − сложение ассоциативно;

x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);

x + (− x ) = 0 − для каждого элемента x из L существует единственный противоположный элемент − x ( x + (− x ) = 0 для любого x из L).

2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x , причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно : ;

1· x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y ) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.

Матрица линейного преобразования.

Линейными операциями называются операции сложения матриц и умножение матрицы на число.

Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соот ветствующих элементов слагаемых . Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число

элемент которой равен сумме соответствующих элементов слагаемых:

12. Характеристические числа и собственные векторы линейного преобразования.

Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор 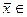L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:A .

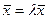При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору 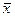.