Принцип управления по отклонению

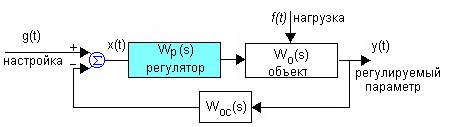Система описывается передаточной функцией разомкнутой системы и уравнением замыкания: x(t) = g(t) - y(t) W_oc(t). Алгоритм работы системы заключен в стремлении свести ошибку x(t) к нулю.

Достоинства:

• ООС приводит к уменьшению ошибки не зависимо от факторов ее вызвавших (изменений параметров регулируемого объекта или внешних условий).

Недостатки:

• В системах с ОС возникает проблема устойчивости.
• В системах принципиально невозможно добиться абсолютной инвариантности к возмущениям. Стремление добиться частичной инвариантности (не 1-ыми ОС) приводит к усложнению системы и ухудшению устойчивости.

Комбинированное управление

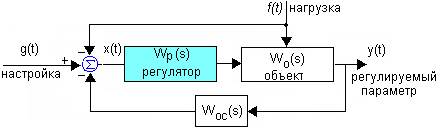
Комбинированное управление заключено в сочетании двух принципов управления по отклонению и внешнему возмущению. Т.е. сигнал управления на объект формируется двумя каналами. Первый канал чувствителен к отклонению регулируемой величины от задания. Второй формирует управляющее воздействие непосредственно из задающего или возмущающего сигнала.

x(t) = g(t) - f(t) - y(t)Woc(t)

Достоинства:

• Наличие ООС делает систему менее чувствительной к изменению параметров регулируемого объекта.
• Добавление канала(ов), чувствительного к заданию или к возмущению, не влияет на устойчивость контура ОС.

Недостатки:

• Каналы, чувствительные к заданию или к возмущению, обычно содержат дифференцирующие звенья. Их практическая реализация затруднена.
• Не все объекты допускают форсирование.

Анализ устойчивости САР

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.

Понятие устойчивости можно распространить и на случай движения САР:

• невозмущенное движение,
• возмущенное движение.

Движение любой СУ описывается с помощью дифференциального уравнения, которое в общем случае описывает 2 режима работы системы:

- режим установившегося состояния

- режим движения

При этом общее решение в любой системе можно записать в виде:

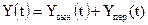
Вынужденная составляющая определяется входным воздействием на вход СУ. Этого состояния система достигает по окончании переходных процессов.

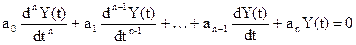Переходная составляющая определяется решением однородного дифференциального уравнения вида:

Коэффициенты a₀,a₁,…a_n включают в себя параметры системы => изменение любого коэффициента дифференциального уравнения приводит к изменению целого ряда параметров системы.

Решение однородного дифференциального уравнения

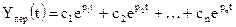
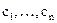
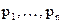
где постоянные интегрирования, а – корни характеристического уравнения следующего вида:

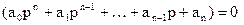
Характеристическое уравнение представляет собой знаменатель передаточной функции приравненный к нулю.

Корни характеристического уравнения могут быть вещественными, комплексно-сопряженными и комплексными, что определяется параметрами системы.

Чтобы оценивать устойчивость систем, разработан ряд критериев устойчивости

Все критерии устойчивости делятся на 3 группы:

- корневые

- алгебраические

- частотные