Пример. Даны матрицы А и В. ; .
Найти произведение матриц АВ.
Решение:
АВ= 
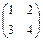 ·
· 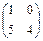 =
= 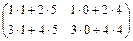 =
= 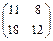
Пример . Даны матрицы А и В. А = 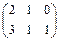 и В =
и В = 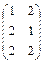 .
.
Решение: А = (2X3), В = (3X2) => АВ = (2X2)
АВ= 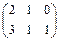 ·
· 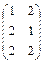 =
= 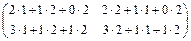 =
= 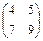
Свойства умножения матриц:
1) АВ¹ВА;
2) (АВ)С=А(ВС);
3) АЕ=ЕА=А
4) (АВ)k = (AB)k= A(Bk)
5) (A+B)C = AB +BC
6) A(B+C) = AB + AC/
Транспонированной матрицей АT называется матрица, у которой строки записаны вместо столбцов, а столбцы – вместо строк.
Пример. Пусть дана матрица А= 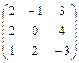 , тогда
, тогда
АT = 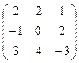
Определители.
Определителем второго порядка, соответствующий матрице А = 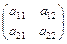 , называется число
, называется число 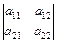 =а11а22 - а12а21.
=а11а22 - а12а21.
Пример. Вычислить определителем второго порядка.
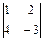 = 1 · (-3) – 2 · 4 = -11.
= 1 · (-3) – 2 · 4 = -11.
Определителем третьего порядка, соответствующий матрице
А = 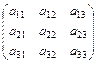 , называется число
, называется число 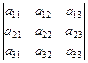 = а11а22а33+а12а23а31+ а13а21а32 - а13а22а31 - а12а21а33 –а11 а23а32.
= а11а22а33+а12а23а31+ а13а21а32 - а13а22а31 - а12а21а33 –а11 а23а32.
Чтобы запомнить какие произведения в правой части равенства следует брать со знаком «+», а какие со знаком «-», полезно правило названное правилом треугольника, изображенное на рис. 1.
 |
« + » « - »
Рисунок 1.
Пример. Вычислить определитель
Второй способ вычисления определителей третьего порядка – это способ вычисления определителей третьего порядка, заключается в дописывании первых двух столбцов, в нахождении произведений по главной диагонали и параллелях к ней и по побочной диагонали и параллелях к ней.
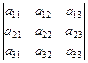
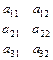 = а11а22а33+а12а23а31+ а13а21а32 - а13а22а31 - а12а21а33 –а11 а23а32.
= а11а22а33+а12а23а31+ а13а21а32 - а13а22а31 - а12а21а33 –а11 а23а32.
Свойства определителей:
1) Если в определителе поменять местами две строки (столбца), то его знак изменится на противоположный.
2) Если в определителе поменять местами строки и столбцы, то его знак и величина не изменится.
3) Если в определителе две строки пропорциональны (равны), то он равен нулю.
4) Если в определителе какую либо строку (столбец) умножить на некоторое число и сложить с другой строкой (столбцом), то его значение не изменится.
5) Если в определителе элементы какой либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
6) Если определитель содержит нулевую строку или столбец, то он равен нулю.
Минором Мij элемента определителя аij называется определитель, получаемый из исходного путем вычеркивания i- ой строки и j-ого столбца на которых расположен этот элемент.
Алгебраическим дополнением Аij элемента определителя аij называется минор умноженный на (-1)i+j.
Третий способ вычисления определителей – с помощью теоремы разложения.
Теорема разложения: Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
Пример. Вычислить определитель третьего порядка 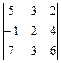 , разложив определитель по элементам первой строки.
, разложив определитель по элементам первой строки.
Решение:
Способ 1.
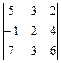 = 5· (-1)1+1·
= 5· (-1)1+1· 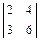 + 3 · (-1)1+2 ·
+ 3 · (-1)1+2 · 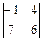 + 2·(-1)1+3 ·
+ 2·(-1)1+3 · 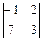 = 68.
= 68.
Этот же определитель можно вычислить с помощью свойства 4), а затем применить теорему разложения. В нашем примере образуем нули в первом столбце. Для этого к элементам первой строки прибавим элементы второй строки, умноженной на 5, а к элементам третьей строки прибавим элементы второй строки, умноженной на 7. И полученную матрицу разложим по элементам первого столбца.
Решение:
Способ 2.
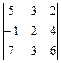 =
= 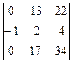 = 0
= 0 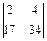 - (-1)
- (-1) 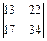 +0
+0 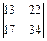 =
= 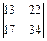 =13 · 34 – 17 · 22 = 68.
=13 · 34 – 17 · 22 = 68.
