Моделирование случайных величин

Для моделирования случайной величины необходимо знать ее закон распределения. Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, в основе которого лежит их формирование из исходной последовательности случайных чисел, распределенных в интервале [0, 1] по равномерному закону.

Равномерно распределенные в интервале [0, 1] последовательности случайных чисел можно получить тремя способами:

- использование таблиц случайных чисел (табличный способ);

- применение генераторов случайных чисел (аппаратный способ);

- метод псевдослучайных чисел (программный способ).

Табличный способ

При решении задачи без применения ЭВМ чаще всего используют таблицы случайных чисел. В таблицах случайных чисел случайные цифры имитируют значения дискретной случайной величины с равномерным распределением:

					…
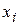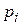	0.1	0.1	0.1	0.1	…	0.1

При составлении таких таблиц выполняется требование, чтобы каждая из этих цифр 0; 1; ...; 9 встречалась примерно одинаково часто и независимо от других с вероятностью .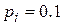

Самая большая из опубликованных таблиц случайных чисел содержит 1000 000 цифр. Таблицы случайных чисел требуют тщательной проверки с помощью специальных статистических тестов.

Аппаратный способ

При решении задач на ЭВМ для выработки случайных чисел, равномерно распределенных в интервале [0, 1], могут применяться генераторы случайных чисел. Данные генераторы преобразуют результаты случайного физического процесса в двоичные числа. В качестве случайного физического процесса обычно используют собственные шумы (случайным образом меняющееся напряжение), явления распада радиоактивных элементов и т.д.

Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны:

- состоять из квазиравномерно распределенных чисел;

- содержать статистически независимые числа;

- быть воспроизводимыми;

- иметь неповторяющиеся числа;

- получаться с минимальными затратами машинного времени;

- занимать минимальный объем машинной памяти.

Недостатки данного способа получения случайных чисел следующие:

- трудно проверить качество вырабатываемых чисел;

- случайные числа не воспроизводимы (если их не запоминать), следовательно, нельзя повторить расчет для исключения случайного сбоя.

Алгоритмический способ

Получение случайных чисел с равномерным законом распределения заключается в выработке псевдослучайных чисел. Псевдослучайные числа – это числа, полученные по какой-либо формуле и имитирующие значения случайной величины. В практике моделирования применяются генерации последовательностей псевдослучайных чисел с помощью алгоритмов вида:

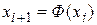. (8.3)

Данные алгоритмы представляют рекуррентные соотношения первого порядка, для которых начальное число x₀ и постоянные параметры уже заданы.