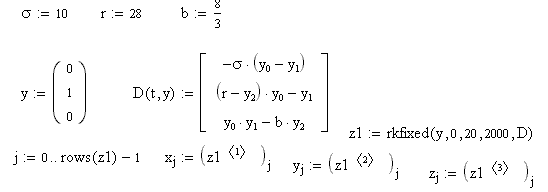Системы дифференциальных уравнений первого порядка

Дана система n уравнений первого порядка

y_i' = f_i(x, y₁, y₂, ¼, y_n), i = 1, 2, ¼, n (4.2)

и начальные условия

y₁(x₀) = y₁₀, y₂(x₀) = y₂₀, ¼, y_n(x₀) = y_n0. (4.3)

Для отыскания численного решения системы (4.2) с начальными условиями (4.3) вычисляют для некоторых значений аргумента x₁, x₂, ¼, x_N (x₀ < x₁ < x₂ < ¼ < x_N) значений функций y₁(x), y₂(x), ¼, y_n(x), являющиеся искомым решением, т.е. составляют n таблиц

[y_i(x₁), y_i(x₂), ¼, y_i(x_N)] i = 1, 2, ¼, n.

К данной задаче применимы все методы, рассмотренные для случая одного дифференциального уравнения, если в вышеприведённых формулах заменить y_k на y_ik (y_ik = y_i(x_k)) и f_k на f_ik (f_ik = f_i(x_k, y_1k, y_2k, ¼, y_nk)). Например, расчётная формула метода Эйлера (2) для системы запишется так

{y_{i (k+1)} = y_ik + hf_ik} i = 1, 2, ¼, n.

Дифференциальные уравнения второго порядка

Дано дифференциальное уравнение

y '' = f(x, y, y ') (4.4)

и начальные условия

y(x₀) = y₀, y '(x₀) = y₀'. (4.5)

Для отыскания численного решения этой задачи требуется составит таблицу значений функции y = y(x), являющейся искомым решением, для некоторой последовательности значений аргумента x₁, x₂, ¼, x_n (x₀ < x₁ < x₂ < ¼ < x_n). Иногда требуют также составления таблицы производной y '(x).

Метод приведения к системам уравнений первого порядка

Ведём обозначение

y ' = z.

Решение дифференциального уравнения (4.4) с начальными условиями (4.5) сводится к решению следующей системы обыкновенных дифференциальных уравнений первого порядка с указанными начальными условиями:

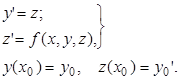
Метод Рунге – Кутты

Схема Рунге – Кутты с четырьмя подстановками, имеющая погрешность порядка h⁵:

	x	v0 = y	v1 = hy '	k =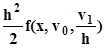
	x0	v00	v10	k1
	x0 + h/2	v00 + v10/2 + k1/4	v10 + k1	k2
	x0 + h/2	v00 + v10/2 + k2/4	v10 + k2	k3
	x0 + h	v00 + v10 + k3	v10 + 2k3	k4
	x1 = x0 + h	v01 = v00 + v10 + k(0)	v11 = v10 + k(1)
	k(0) = (k1 + k2 + k3)/3, k(1) = (k1 +2k2 + 2k3 + k4)/3

Метод конечных разностей

Экстраполяционные формулы Фалькнера:

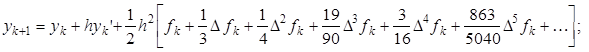
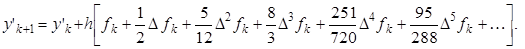
Интерполяционные формулы Фалькнера:

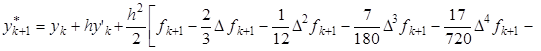
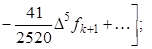
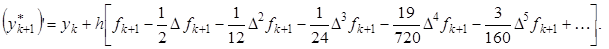
При использовании данных разностных формул следует поступать так же, как в методе Адамса (7).

Задание № 8

Найти одним из методов решение задачи Коши на промежутке [0, a]. Конец промежутка интегрирования a указан для каждой задачи. Решение получить с 5 верными знаками после запятой.

В отчёте привести программу решения задачи, таблицу значений функции и график функции. Проверить результаты решения, используя какой-либо из математических пакетов.

Вариант А

Вариант	Уравнения задачи	a	b	а
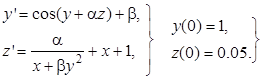		1.1	2.1	0.4
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
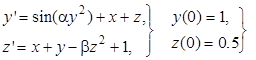		1.1	2.1	0.4
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
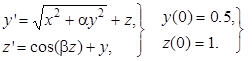		1.1	2.1	0.6
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
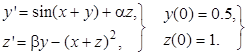		1.1	2.1	0.6
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
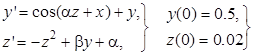		1.1	2.1	0.4
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-

Вариант Б

Вариант	Уравнения задачи	a	b	а
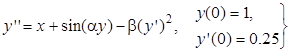		1.1	2.1	0.8
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
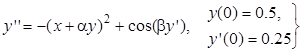		1.1	2.1	0.8
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
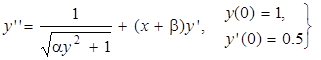		1.1	2.1	0.5
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
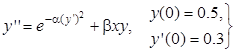		1.1	2.1	0.8
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-
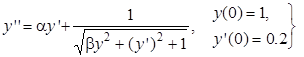		1.1	2.1	1.0
	-"-	1.2	2.2	-"-
	-"-	1.3	2.3	-"-
	-"-	1.4	2.4	-"-
	-"-	1.5	2.5	-"-

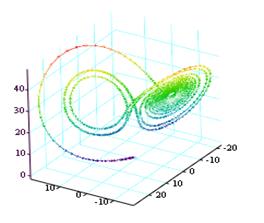
Замечание 1. В рамках математических пакетов численное решение систем дифференциальных уравнений первого порядка отличается только размерностью векторов и матриц. Например, в рамках пакета Mapleрешение системы трёх ОДУ выглядит следующим образом:

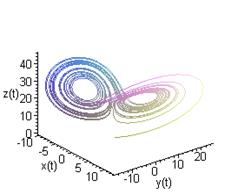
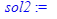
Отличительной особенностью пакета Mapleявляется то, что в его рамках можно численно решать ОДУ произвольного порядка, не разделяя его на систему ОДУ первого порядка. Ниже приведён подробный пример решения такого уравнения.

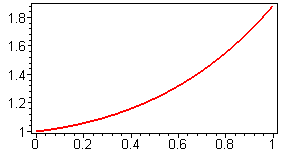
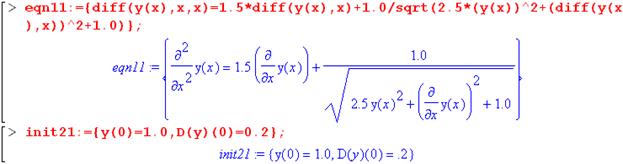
Замечание 2. Отмеченное выше справедливо и для пакета Mathcad, поэтому ниже мы приведём лишь команды решения уравнений без таблицы значений функции. В данном пакете важно то обстоятельство, что для пространственных кривых используется Scatterplot/