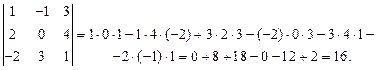Скалярное произведение двух векторов
Скалярным произведением векторов 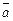 = (х1, х2, …, хп) и
= (х1, х2, …, хп) и 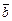 = (у1,
= (у1,
у2, …, уп) называется число 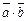 , равное сумме произведений соответствующих координат векторов
, равное сумме произведений соответствующих координат векторов 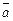 и
и 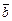 :
:
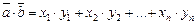 .
.
Скалярное произведение векторов обладает следующими свойствами:
1. 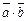 =
= 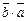 .
.
2. 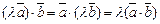 ,
, 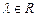 .
.
3. 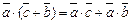 .
.
4. 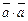
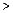 0, если
0, если 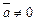 , и
, и 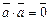 , если
, если 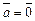 .
.
Линейная зависимость и линейная независимость векторов
Линейной комбинацией векторов 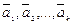 называется вектор вида
называется вектор вида
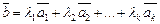 , (1)
, (1)
где 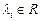 ,
, 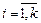 .
.
Пример. Пусть 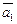 = (2;1;0),
= (2;1;0), 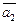 = (1;0;1),
= (1;0;1), 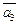 = (0;1;2). Вектор
= (0;1;2). Вектор 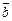 = (0;4;4) — линейная комбинация векторов
= (0;4;4) — линейная комбинация векторов 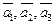 , так как
, так как 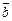 = 1·
= 1· 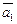 –2 ·
–2 · 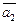 + 3 ·
+ 3 · 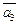 .
.
В случае выполнения равенства (1) говорят, что вектор 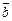 линейно выражается через векторы
линейно выражается через векторы 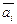 ,
, 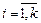 или разлагается по этим
или разлагается по этим
векторам.
Система ненулевых векторов вида
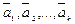 (2)
(2)
называется линейно зависимой, если существуют числа 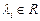 ,
, 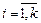 , не все равные нулю, такие, что
, не все равные нулю, такие, что
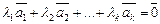 . (3)
. (3)
Если же равенство (3) для данной системы векторов 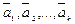 возможно лишь при
возможно лишь при  , то эта система векторов называется линейно независимой.
, то эта система векторов называется линейно независимой.
Базис и ранг системы векторов
Пусть дана система векторов (2).
Максимальной линейно независимой подсистемой системы векторов (2) называется такой частичный набор векторов этой системы, который удовлетворяет следующим условиям:
1. Векторы этого набора линейно независимы.
2. Любой вектор системы (2) линейно выражается через векторы этого набора.
Максимальная линейно независимая подсистема системы векто-
ров (2) называется ее базисом.
Будем называть рангом системы векторов число векторов ее базиса.
Система векторов называется базисом пространства Rn, если:
1. Векторы этой системы линейно независимы.
2. Всякий вектор из Rn линейно выражается через векторы данной системы.
Матрицы
Прямоугольная таблица чисел вида
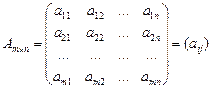 ,
,
состоящая из m строк и n столбцов, называется матрицей 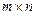 .
.
Здесь aij — действительные числа (i = 1, 2, …, m, j = 1, 2,…, n), которые называются элементами матрицы. Индекс i указывает на номер строки, а индекс j — номер столбца. На их пересечении находится элемент aij.
Матрица, все элементы которой являются нулями, называется нулевой.
В случае, когда т = п (число строк равно числу столбцов), матрица А называется квадратной матрицей n-го порядка:
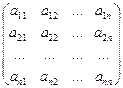 .
.
Главной диагональю квадратной матрицы называется ее диагональ, составленная из элементов a11, a22,…, ann.
Квадратная матрица 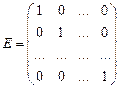 называется единичной, если элементы ее главной диагонали равны единице, а все остальные элементы — нулю.
называется единичной, если элементы ее главной диагонали равны единице, а все остальные элементы — нулю.
Очевидно, строки матрицы An´m образуют систему n-мерных векторов 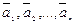 .
.
Рангом матрицы 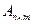 назовем ранг этой системы
назовем ранг этой системы 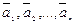 .
.
Следующие преобразования матрицы А назовем элементарными:
1. Перестановка местами двух ее строк (столбцов).
2. Умножение всех элементов строки (столбца) матрицы на одно и то же число, отличное от нуля.
3. Прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и тоже число.
Теорема. При элементарных преобразованиях ранг матрицы не изменяется.
Для практического вычисления ранга матрицы A ее удобно при помощи элементарных преобразований приводить к виду
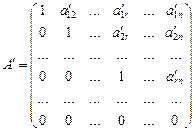 .
.
Тогда ранг матрицы А равен числу единиц на диагонали матрицы A', т. е. числу r.
Действия над матрицами
Суммой двух матриц Ап´т = (аij) и Bп´т = (bij) называется такая третья матрица Сп´т = (сij), что сij = аij + bij.
Произведением матрицы Ап´т = (аij) на число 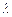 называется такая матрица Bп´т =
называется такая матрица Bп´т = 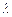 · Ап´т = (dij), что dij =
· Ап´т = (dij), что dij = 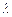 · аij.
· аij.
Пример. Если 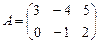 ,
, 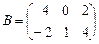 , то С = 2А – 3В = =
, то С = 2А – 3В = = 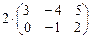
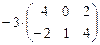 =
= 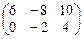 +
+ 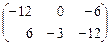 =
=
= 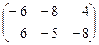 .
.
Произведением матриц Ап´т = (аij) и Bm´k = (bij) называется такая третья матрица Сп´k = (сij), что cij = аi1 · b1j + аi2 · b2j +…+ аim · bmj .
Пример. Если 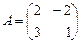 ,
, 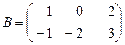 , то C = A · B =
, то C = A · B =
= 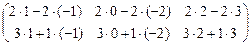 =
= 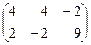 .
.
Определители
Квадратной матрице А порядка п можно сопоставить число det A (или |A|, или 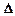 ), называемое ее определителем, следующим образом:
), называемое ее определителем, следующим образом:
1. Если п = 1, A = (a11), тогда определитель первого порядка имеет вид
|A| = 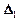 = |a11| = a11.
= |a11| = a11.
2. Если п = 2, 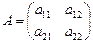 , тогда определитель второго порядка вычисляется по формуле
, тогда определитель второго порядка вычисляется по формуле
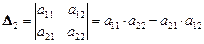 .
.
3. Если п = 3, 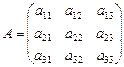 , то матрице третьего порядка соответствует определитель
, то матрице третьего порядка соответствует определитель
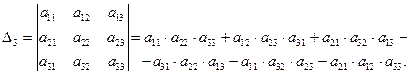
Это выражение получается по правилу треугольников (правилу Саррюса). Его можно пояснить схемами, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками (рис. 9).
 |
| Рис. 9 |
Пример.