Геометрические и физические задачи

При решении геометрических задач, в которых требуется найти уравнение кривой по заданным свойствам ее касательной, нормали или ограниченной ею криволинейной трапеции, используется геометрическое истолкование производной (угловой коэффициент касательной) и интеграла с переменным верхним пределом (площадь криволинейной трапеции с подвижной ограничивающей ординатой).

Пример 3.Найти уравнение кривой, проходящей через точку (0,-2), для которой угловой коэффициент касательной в любой точке на три единицы больше ординаты точки касания.

Решение.Пусть 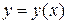– искомая кривая. Исходя из геометрического смысла производной, можем записать

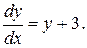
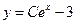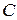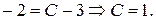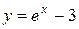Разделяя переменные и интегрируя, получим общее решение уравнения . Поскольку кривая должна проходить через точку (0,-2), то для получаем уравнение Итак, – искомая кривая.

Пример 4. Найти уравнение кривой, проходящей через точку (1,1), если для любого отрезка 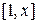площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, в два раза больше произведения координат точки 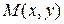кривой ( , ).

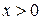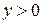Решение. Согласно условию задачи имеем

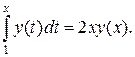
Дифференцируя это равенство по 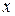, получаем дифференциальное уравнение 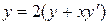, которое приводится к виду

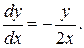
Интегрируя это уравнение и учитывая начальное условие 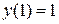, получаем уравнение искомой кривой: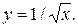

Общего метода составления дифференциальных уравнений для описания различных физических процессов не существует. Можно лишь дать некоторые указания. Пусть 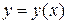– искомая зависимость между характеристикам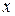и и 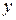изучаемого процесса. При составлении дифференциального уравнения, решением которого является функция 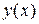, необходимо выразить приращение 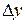этой функции через приращение 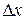независимой переменной, то есть выразить разность 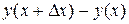через величины, о которых говорится в задаче. Разделив эту разность на 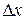и перейдя к пределу при 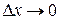, получим дифференциальное уравнение, описывающее изучаемый процесс. Во многих случаях искомая зависимость определяется исходя из закона или экспериментального факта, установленного для той или иной области естествознания.

Пример 5.Тело, имеющее в начальный момент температуру 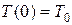, поместили в среду, температура которой поддерживается неизменной и равна 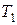. Как будет меняться с течением времени температура тела, если скорость ее изменения пропорциональна разности температур тела и окружающей среды.

Решение.Пусть 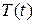– температура тела в момент времени 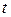. По условию задачи

,

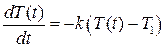где 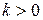– коэффициент пропорциональности. Разделяя переменные, получим

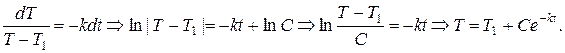
Учитывая начальное условие 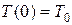, находим искомую зависимость

.

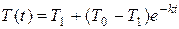Пример 6.Сосуд, площадь 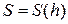поперечного сечения которого есть известная функция высоты 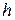, наполнен жидкостью до высоты H. В дне сосуда имеется отверстие площадью 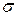, через которое жидкость вытекает. Определить время 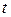, за которое уровень жидкости понизится от начального положения до произвольного 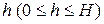и время полного опорожнения сосуда, если известно, что скорость истечения жидкости через отверстие, находящееся не расстоянии 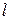ниже уровня жидкости равна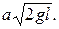

Решение. Пусть высота жидкости в сосуде в некоторый момент времени 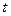равна 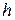. Количество жидкости 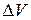, вытекающее из сосуда за промежуток времени 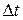численно равно объему цилиндра с площадью основания 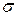и высотой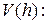 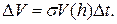Этот же объем может быть вычислен другим способом. За указанный промежуток времени уровень жидкости понизится на величину 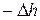. Поэтому 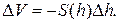Итак, 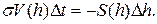Разделив обе часть последнего равенства на 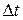и переходя к пределу при 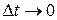, получим дифференциальное уравнение

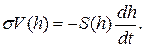
По условию задачи 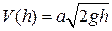. Разделяя переменные, получим

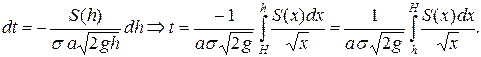
Полагая 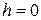, находим время полного опорожнения сосуда

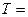
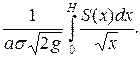
Задание 1[1]

В задачах 1-3 принять, что скорость нагревания (остывания) тела пропорциональна разности температур тела и окружающей среды.

1. Тело охладилось за 10 минут от 100⁰ до 60⁰. Температура окружающего воздуха поддерживается равной 20⁰. Когда тело остынет до 25⁰?

2. В сосуд, содержащий 1 кг воды при температуре 20⁰, опущен алюминиевый предмет с массой 0,5 кг, удельной теплоемкостью 0,2 и температурой 75⁰. Через минуту вода нагрелась на 2⁰. Когда температура воды и предмета будет отличаться одна от другой на 1⁰? Потерями тепла на нагревание сосуда и прочими пренебречь.

3. Кусок металла с температурой a градусов помещен в печь, температура которой в течение часа равномерно повышается от a градусов до b градусов. При разности температур печи и металла в Т градусов металл нагревается со скоростью kТ градусов в минуту. Найти температуру металла через час.

4. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/сек, через 4 сек. скорость ее 1 м/сек. Когда скорость лодки уменьшится до 1 см/сек? Какой путь может пройти лодка до остановки?

В задачах 5-6 использовать закон радиоактивного распада: количество радиоактивного вещества, распадающегося в единицу времени пропорционально количеству вещества, имеющемуся в рассматриваемый момент.

5. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько дней останется 1% от первоначального количества вещества?

6. Согласно опытам, в течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия?

7. Пуля, двигаясь со скоростью 400 м/сек пробивает стену толщиной 20 см и вылетает, имея скорость 100 м/сек. Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, найти время прохождения пули через стену.

8. Парашютист прыгнул с высоты 1,5 км, а раскрыл парашют на высоте 0,5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50 м/сек. Изменением плотности воздуха с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости. (g=10 м/сек)

9. Футбольный мяч весом 0,4кГ брошен вверх со скоростью 20 м/сек. Сопротивление воздуха пропорционально квадрату скорости и равно 0.48 Г при скорости 1 м/сек. Вычислить время подъема мяча на наибольшую высоту. Как изменятся эти результаты, если пренебречь сопротивлением воздуха? ( 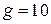м/сек).

В задачах 10-13 принять, что жидкость из сосуда вытекает со скоростью равной 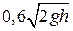, где 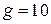м/сек., h – высота уровня воды над отверстием.

10. За какое время вытечет вода из цилиндрического бака диаметром 1,8 метра и высотой 2,45 метра через отверстие в дне диаметром 6 см.

11. Цилиндрический бак поставлен вертикально и имеет отверстие в дне. Половина воды из полного бака вытекает за 5 минут. За какое время вытечет вся вода?

12. Воронка имеет форму конуса радиуса 6 см и высоты 10 см, обращенного вершиной вниз. За какое время вытечет вся вода из воронки через круглое отверстие диаметра 0,5 см, сделанное в вершине конуса.

13. В прямоугольный бак размером 60см на 75см и высотой 80 см поступает 1,8 л воды в секунду. В дне имеется отверстие площадью 2,5 см². За какое время наполнится бак?

14. Найти кривую, у которой отрезок нормали в любой точке кривой, заключенный между осями координат, делится пополам в этой точке.

15. Найти уравнение кривой, проходящей через точку (3,1), для которой отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью .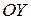

16. Найти уравнение кривой, проходящей через точку (2,0), если отрезок касательной к кривой между точкой касания и осью 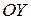имеет постоянную длину 2.

17. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.

18. Найти кривую, для которой площадь S области, заключенная между этой кривой, осью ОХ и прямым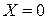и и 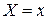есть заданная функция .

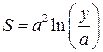19. Доказать, что кривая, все нормали к которой проходят через фиксированную точку, есть окружность.

20. Найти уравнение кривой, проходящей через точку 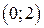, если площадь криволинейной трапеции, ограниченной дугой этой кривой, в два раза больше длины соответствующей дуги.

21. Найти кривую, проходящую через точку 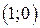, если длина отрезка оси абсцисс, отсекаемая ее нормалью, на 2 больше абсциссы точки касания.

22. Диск, начавший вращаться с угловой скоростью 5 оборотов в секунду, через 3 минуты вращается со скоростью 2 об/сек. Через сколько времени после начала вращения он будет вращаться со скоростью 1 об/сек если сила трения пропорциональна угловой скорости вращения.

23. Материальная точка движется прямолинейно, причем так, что ее кинетическая энергия в момент 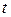прямо пропорциональна средней скорости движения в интервале времени от нуля до t. Известно, что при 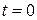путь 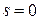. Показать, что движение равномерно.

24. Моторная лодка движется по озеру со скоростью 20 км/час. Через 40 с. после выключения двигателя ее скорость уменьшается до 8 км/час. Сопротивление воды пропорционально скорости движения лодки. Какова скорость лодки через две минуты после выключения двигателя?

25. В резервуар, в котором находится 100 л. 10% -го раствора соли, каждую минуту вливается 30 л. воды и выливается 20 л. смеси. Какое количество соли останется в резервуаре через 10 минут (смесь непрерывно перемешивается)?

26. Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 4.

27. Найти кривые, для которых сумма катетов треугольника, построенного как в задаче 26, есть величина постоянная, равная 2.

28. Количество света, поглощаемого слоем воды малой толщины пропорционально количеству падающего света и толщине слоя. Слой воды толщиной 35 см поглощает половину падающего на нее света. Какую часть света поглотит слой толщиной 2 м.

29. Найти уравнение кривой, проходящей через начало координат, если для любого отрезка 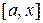площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, равна кубу ординаты концевой точки дуги.

30. Найти кривые, обладающие следующим свойством: если через любую точку кривой провести прямые, параллельные осям координат, до встречи с этими осями, то площадь полученного прямоугольника делится кривой в отношении 1:2.

31. Найти кривые, обладающие следующим свойством: отрезок оси абсцисс, отсекаемый касательной и нормалью, проведенными из произвольной точки, равен 4.