Тема 3. Системы линейных алгебраических уравнений
Методы решения систем уравнений
I. Метод обратной матрицы (матричный метод).
Пример 1. Решить систему матричным методом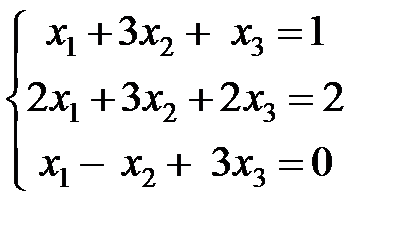 
.
Решение:Для данной системы: матрица системы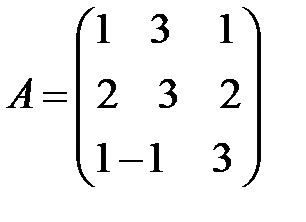 
,
матрицы-столбцы свободных членов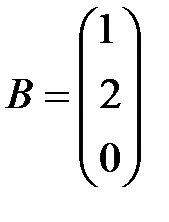 
и неизвестных 
.
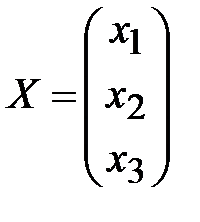Для нахождения решения по формуле (2.6), необходимо найти для матрицы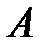 
обратную, которая уже найдена в примере 11 темы 1:
.
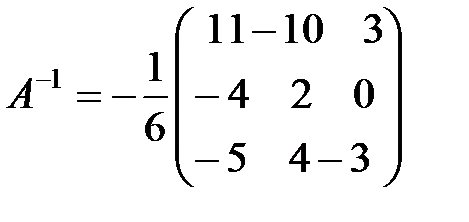Следовательно, решение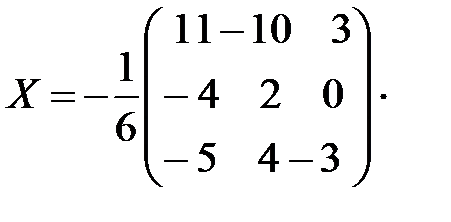 
= 
= 
.
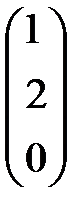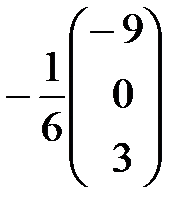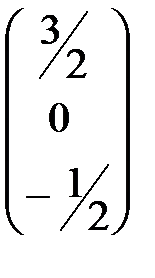Итак,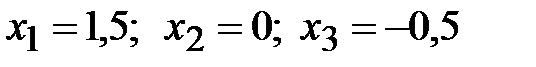 
, или 
.
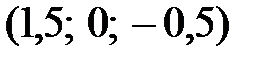II. Метод Крамера (решение СЛУ по формулам Крамера).
Пример 2. Решить систему по формулам Крамера
.
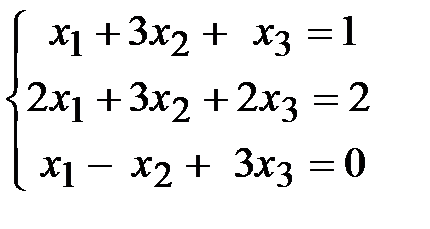Решение:Для данной системы формулы Крамера (2.7) будут иметь вид: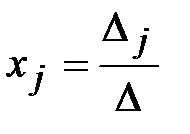 
, где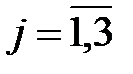 
. Вычислим 
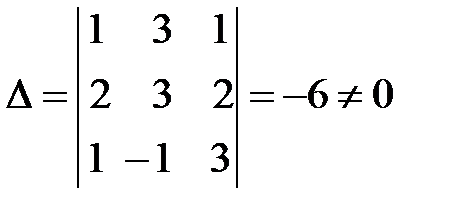. Следовательно,
система имеет единственное решение.
Вычислим все три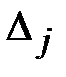 
, которые получаются из определителя 
заменой 
–го столбца столбцом свободных членов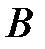 
.
; 
; 
. 
; 
; 
.
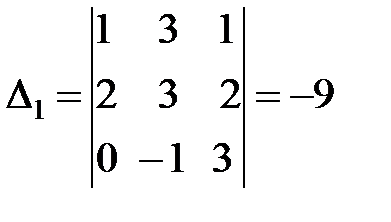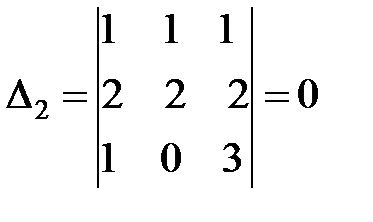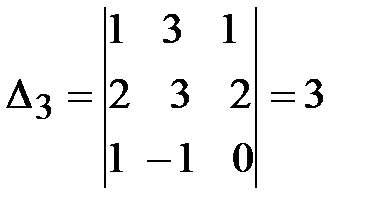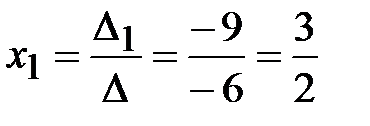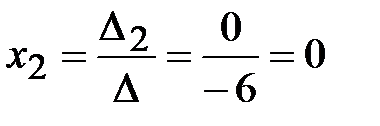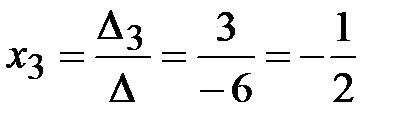Итак, .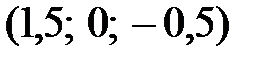
Полученное решение совпадает с решением этой же системы матричным методом (пример 1).
III. Метод Гаусса и Жордана-Гаусса.
Решение системы методом обратной матрицы и по формулам Крамера часто оказывается трудоемкой задачей и применимо лишь когда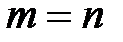 
, более универсальный и эффективный метод (легко реализуемый на компьютере) – метод Гаусса или метод Жордана-Гаусса.
В основе этих методов лежат элементарные преобразования систем, в результате которых, из исходной системы уравнений получают эквивалентную ей систему специального вида, а именно: с матрицей треугольного (метод Гаусса) или диагонального (метод Жордана-Гаусса) вида.
К элементарным преобразованиям систем относятся:
1) перестановка строк;
2) умножение всех элементов строки на число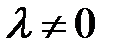 
;
3) прибавление к элементам любой строки соответствующих элементов другой строки, умноженных на число ;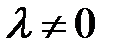
4) исключение из матрицы нулевой строки.
Замечание. Если в процессе преобразований получается строка, которой соответствует уравнение вида: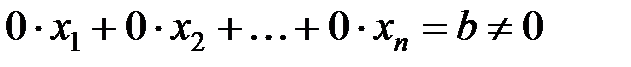 
, то система несовместна.
Применяя эти методы, следует записать расширенную матрицу СЛУ и с помощью элементарных преобразований привести матрицу системы к треугольному виду (метод Гаусса), где все элементы ниже главной диагонали станут нулевыми. Затем записать СЛУ и с помощью так называемого «обратного хода» найти неизвестные. А именно: из последнего уравнения определяют неизвестное. Найденное значение подставляют в предыдущее уравнение и решают его, и т.д. продолжают находить все неизвестные СЛУ.
Преобразовывая расширенную матрицу системы по методу Жордана-Гаусса, добиваются того, чтобы матрица СЛУ имела диагональный вид. Далее записывают СЛУ по преобразованной матрице, и все неизвестные будут определены.