ТЕМА 2. Системы линейных алгебраических уравнений

Пусть задана система m линейных алгебраических уравнений с n неизвестными (СЛАУ):

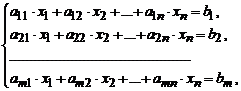
где 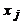– неизвестные, 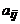– коэффициенты при неизвестных, 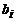– свободные члены, , .

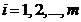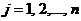Обозначим через A матрицу, составленную из коэф-фициентов при неизвестных 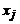, а через 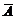– матрицу, полу-ченную из A присоединением к ней столбца свободных членов:

, , .

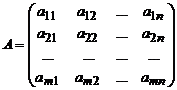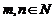Матрица A называется матрицей коэффициентов системы уравнений, а матрица – расширенной матрицей коэффици-ентов системы уравнений.

Определение. Решением системы уравнений называется совокупность таких значений неизвестных: 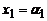, , 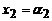…, , 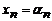которые удовлетворяют всем уравнениям системы. Ре-шить систему уравнений – значит указать все его решения или показать, что их нет.

Определение. Система уравнений называется совместной, если она имеет хотя бы одно решение. Если система не имеет решения, то она называется несовместной.

Теорема 2.1 (Кронекера – Капелли)

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы коэффициентов A ра-вен рангу расширенной матрицы коэффициентов 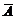. При этом если ранг матрицы A равен рангу матрицы 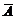и равен числу не-известных, то система уравнений имеет единственное решение; если ранги матриц A и 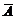равны и меньше числа неизвестных системы, то система уравнений имеет множество решений.

Методы решения системы линейных алгебраических уравнений

Рассмотрим систему из трех линейных алгебраических уравнений и трех неизвестных:

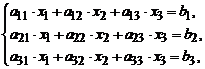(3)

тогда матрица коэффициентов при неизвестных и расширенная матрица коэффициентов имеют вид:

, .

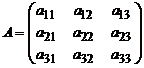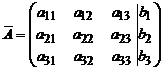Метод Крамера

Для системы (3) введем следующие обозначения:

, ,

, ,

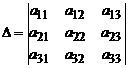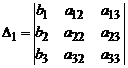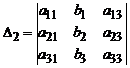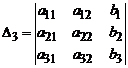где 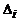, i = 1, 2, 3, – определители, полученные из исходного определителя D заменой i-го столбца столбцом свободных членов.

Тогда при решении системы методом Крамера [2] возможны следующие случаи:

1)если D ¹ 0, то система (3) совместна и имеет единственное решение, которое находится по формулам:

, , ;

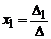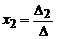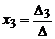2)если D = 0, D₁ = D₂ = D₃ = 0, то система (3) либо имеет множество решений, либо несовместна;

3)если D = 0 и хотя бы один из D₁, D₂, D₃ не равен нулю, то система (3) несовместна и решения не имеет.

Матричный метод

Пусть для системы (3) определитель D ¹ 0. Запишем ее в матричной форме. Имеем: A – матрица коэффициентов при неизвестных, X – столбец неизвестных, B – столбец свободных членов системы:

, , ,

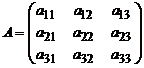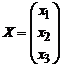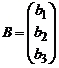тогда

.

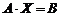Так как умножение матриц некоммутативно (неперестановочно), то, чтобы получить в левой части равенства X, умножим это уравнение н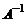а слева

.

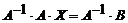Так как 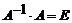, то имеем

,

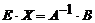или

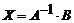. (4)

Метод Гаусса

Метод Гаусса основан на алгоритме последовательного исключения неизвестных.

Выпишем расширенную матрицу коэффициентов системы (3):

.

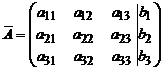Задача состоит в том, чтобы привести ее к «треугольному» виду при помощи эквивалентных преобразований, причем получить единицы на главной диагонали и нули под ними.

Алгоритм состоит в том, что на каждом шаге выполняются следующие действия (количество шагов определяется количеством уравнений). Выбирается одна из ненулевых, не рассмотренных ранее строк, ее номер считаем равным i. Все элементы этой строки делятся на элемент, стоящий на i-м месте (номер столбца этого элемента равен j). Если на i-м шаге какая-то из строк содержит уже на i-м месте единицу, то именно она переставляется и считается i-й строкой. Далее, добавляя к остальным, ранее не рассмотренным строкам i-ю строку, умноженную на подходящее число, добиваемся того, чтобы все элементы j-го столбца, расположенные ниже i-й строки, были равны нулю.

При решении системы уравнений (3) методом Гаусса возможны следующие случаи.

1) Если матрица 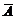приведена к треугольному виду, то система (3) совместна и имеет единственное решение.

2) Если матрица 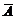содержит хотя бы одну строку, все элементы которой равны нулю, то система (3) совместна и имеет множество решений.

3) Если матрица 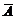содержит строку, все элементы которой кроме свободного члена равны нулю, то система (3) несовместна, то есть решения не имеет.

Пример 2.1. Решить систему уравнений

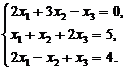
Решение

1) Решим систему методом Крамера.

, ,

, .

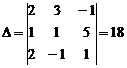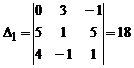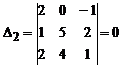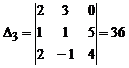Так как D ¹ 0, то система совместна и имеет единственное решение: , , .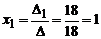

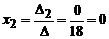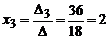2) Решим систему матричным методом.

Так как D ¹ 0, то обратная матрица к матрице A существует. Вычислим алгебраические дополнения, имеем:

;	;	;
;	;	;
;	;	,

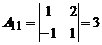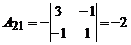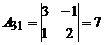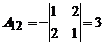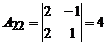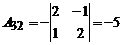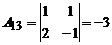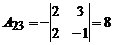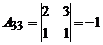тогда обратная матрица 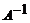имеет следующий вид:

.

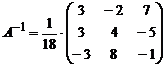Найдем решение системы. Для этого запишем уравнение (4) в координатной форме:

,

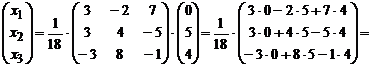
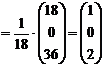следовательно, х₁ = 1, х₂ = 0, х₃ = 2.

3) Решим систему методом Гаусса. Приведем расширенную матрицу коэффициентов 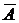к «треугольному виду». Для этого переставим 1-ю и 2-ю строки местами. Затем домножим 1-ю строку на (–2) и прибавим ко 2-й и 3-й строкам. Полученную 2-ю строку домножим на (3) и прибавим к полученной 3-й строке. В итоге последнюю строку разделим на 18.

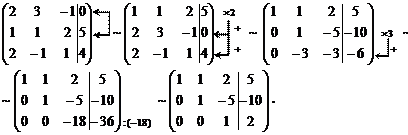
Матрица приведена к треугольному виду, следовательно, сис-тема совместна и имеет единственное решение. Найдем его, выписав систему уравнений, соответствующую последней матрице.

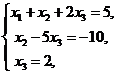Þ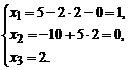

Ответ: х₁ = 1, х₂ = 0, х₃ = 2.

Пример 2.2.Решить систему уравнений

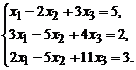
Решение

1) Решим систему методом Крамера, имеем:

, .

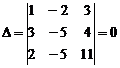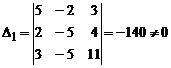Так как D = 0, D₁ ¹ 0, то система несовместна, решения не имеет.

2) Решим систему матричным методом. Так как D = 0, то обратная матрица к матрице A не существует, матричный метод не применим.

3) Решим систему методом Гаусса. Приведем расширен-ную матрицу коэффициентов 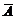к треугольному виду. Для этого домножим 1-ю строку на (–3) и (–2) и прибавим ко 2-й и 3-й строкам соответственно. Полученную 2-ю строку прибавим к полученной 3-й строке:

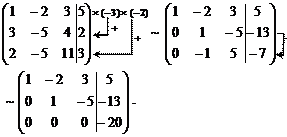
Так как у полученной матрицы в последней строке коэф-фициенты при неизвестных равны нулю, а свободный член не ра-вен нулю, то решения нет, то есть система несовместна.

Ответ: система несовместна.