Неопределённый интеграл
Отыскание функции F(x) по известному дифференциалу dF(x)=f(x)dx (или по известной ее производной F'(x)=f(x)) т.е. действие обратное дифференцированию, называются интегрированием, а искомая функция F(x) называется первообразной функцией от функции f(x).
Определение: Совокупность всех первообразных F(x)+C от функции f(x) называется неопределенным интегралом от этой функции:
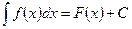
Основные формулы интегрирования.
1. 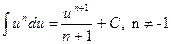
2. 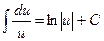
3. 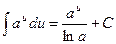
4. 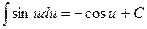
5. 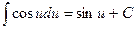
6. 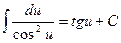
7. 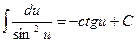
8. 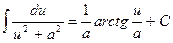
9. 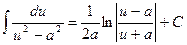
10. 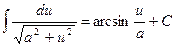
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 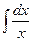 . На основе известной формулы дифференцирования
. На основе известной формулы дифференцирования 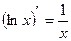 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 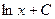 , где С – некоторое постоянное число. Однако, с другой стороны
, где С – некоторое постоянное число. Однако, с другой стороны 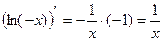 . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод:
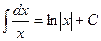
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец, определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 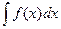 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
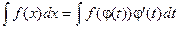
Доказательство: Продифференцируем предлагаемое равенство:
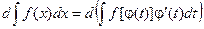
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти неопределенный интеграл 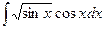 .
.
Сделаем замену t = sinx, dt = cosxdt.
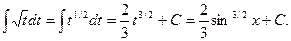
Пример. 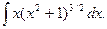
Замена 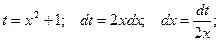 Получаем:
Получаем:
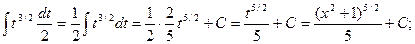
Пример.