Символьное вычисление интегралов

Если есть некоторая функция f(х), то показанный ниже определен­ный интеграл дает значение площади, ограниченной вертикалями а и b, именуемыми пределами интегрирования, кривой f(х) и осью абс­цисс х: 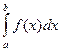. Такой интеграл обычно представляется числом (в общем случае комп­лексным), но может быть представлен и аналитическим выражением. Если f(x)dx есть дифференциал функции F(х), то f(x)dx = dF(x). Функцию F(х) называют первообразной функции f(x). Наиболее об­щий вид первообразной функции f(х) называют неопределенным ин­тегралом и обозначают следующим образом: .

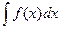В состав этого выражения обычно включается некоторая постоянная интегрирования С, подчеркивающая, что для одной и той же функции f(х) существует масса первообразных, описываемых одной и той же линией, но смещенных по вертикали на произвольную постоянную. О ее существо­вании надо помнить, так как она отдельно в результате не показывается. Возможно также вычисление кратных интегралов, например двойных.

Система Mathcad содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным мето­дом. Ею целесообразно пользоваться, когда нужно просто получить зна­чение определенного интеграла в виде числа. С другой стороны, команда Symbolics (Символьные вычисления) ► Simplify (Упростить) примени­тельно к вычислениям определенных интегралов делает гораздо боль­ше — она ищет аналитическое выражение для интеграла. Более того, она способна делать это и при вычислении кратных интегралов, преде­лы которых — функции.

Как и в случае с вычислением производных, вычисление интегралов с помощью команды Simplify требует записи вычисляемых интегралов в явном виде — с применением шаблонов интегралов.

Расширение выражений

Действие команды Symbolics (Символьные вычисления) ► Expand (Раз­ложить по степеням) в известном смысле противоположно действию команды Symbolics (Символьные вычисления) ► Simplify (Упростить). Подвергаемое преобразованию выражение «расширяется» с использованием известных (и введенных в символьное ядро) соотношений. Разу­меется, расширение происходит только в том случае, когда его резуль­тат однозначен, иначе нельзя считать, что действие этой команды про­тивоположно действию команды Simplify. К примеру, команда Simplify преобразует сумму квадратов синуса и косинуса в 1, тогда как обратное преобразование многозначно и потому в общем виде невыполнимо.

При преобразовании выражений командой Expand система старается более простые функции представить через более сложные, свести ал­гебраические выражения, представленные в сжатом виде, к выражени­ям в развернутом виде и т. д.

Разложение выражений

Команда Symbolics (Символьные вычисления) ► Factor (Разложить множители) используется для факторизации — разложения выраже­ний или чисел на простые множители. Она способствует выявлению математической сущности выражения, например наглядно выявляет представление полинома через его действительные корни, а в том слу­чае, когда разложение части полинома содержит комплексно-сопряжен­ные корни, порождающее их выражение представляется квадратичным трехчленом. В большинстве случаев (но не всегда) операция факторизации ведет к упрощению выражений. Термин «факторизация» не является общепри­знанным в отечественной математической литературе, но мы его остав­ляем в связи с созвучностью англоязычному названию этой операции.

В Mathcad разложение чисел на простые множители записывает­ся как произведение множителей, причем повторяющиеся п раз мно­жители записываются в степени п.