Статистическое распределение

Различают два вида совокупностей однородных объектов:

1. Генеральная – исходное множество объектов с соответствующим признаком, о котором необходимо составить представление;

2. Выборочная (выборка) – сравнительно небольшая часть генеральной совокупности, которая подлежит непосредственному исследованию.

В силу случайного попадания объектов в выборку числовые данные в выборке также случайны.

Задачей математической статистики является отбор выборочной информации и ее обработка, по результатам которой делают выводы о параметрах генеральной совокупности, рассчитываются оценки числовых характеристик распределения генеральной совокупности и устанавливается степень достоверности этих оценок.

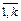Пусть для изучения количественного признака X из генеральной совокупности извлечена выборка x₁, x₂,…, x_k объема n. Наблюдавшиеся значения x_i (i = ) признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом.

где 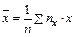– выборочное среднее для вариант (наблюдавшихся различных дискретных значений) x_i компоненты X ( 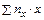- сумма по индексу i произведений вариант x = x_i на соответствующие частоты этих вариант n_x); 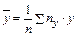– выборочная средняя вариант y = y_j на соответствующие частоты этих вариант n_y; 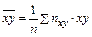( 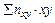– сумма по паре индексов ij произведений x_i×y_j на соответствующие частоты этих пар вариант n_xy); 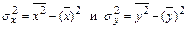– выборочные дисперсии компонент X и Y соответственно;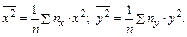

Выборочное линейное уравнение регрессии Y на X имеет вид

,

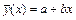где 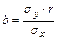– выборочной коэффициент регрессии Y и X; 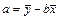; a + bx – линейное приближение условного среднего выборочного 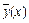, то есть среднего значения случайной переменной Y при условии, что случайная компонента X принимает значение x.

Уравнения регрессии являются математической моделью изучаемой зависимости, исключающей случайные факторы, повлиявшие на полученные результаты.

Рекомендации к решению задачи:

1. Если в корреляционной таблице варианты заданы равноотстоящими соответственно для компоненты X с шагом h₁ и для компоненты Y с шагом h₂, то для упрощения расчетов следует перейти к условным вариантам 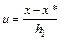, 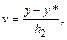где паре вариант x*, y* соответствует максимальная частота n_xy (если максимальная частота n_xy соответствует нескольким парам X = x, Y = y , то выбирается ближайшая к центру корреляционной таблицы). Для новых переменных справедливы следующие соотношения: .

2. Расчеты следует выполнять с учетом правил приближенных вычислений, причем в результатах расчетов после соответствующего округ-

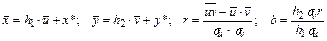6) Искомый доверительный интервал для математического ожидания a имеет вид

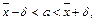
причем 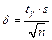(поскольку стандартное отклонение s₀ генеральной совокупности неизвестно).

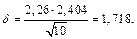
Следовательно, 2 – 1,718 < a < 2 + 1,718 или 0, 282 < а < 3,718.

7) Определим по таблице № 5 Приложений величину q = q(n; g) = = q(10; 0,95) = 0,65.

8) Доверительный интервал для стандартного отклонения s₀ определим согласно неравенству s×(1 – q) < s₀ < s×(1 + q), так как q < 1.

Следовательно, 2,404(1 – 0,65) < s₀ < 2,404(1 + 0,65) или

0,8414< s₀ < 3,9666.

9) Построим полигон частот:

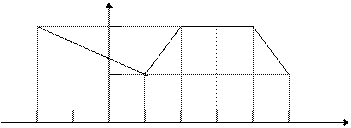n_i

2

х

–2 –1 0 1 2 3 4 5

Рис. 4.

Ответ: 0, 282 < а < 3,718; 0,8414 < s₀ < 3,9666 с надежностью g = 0,95.

Линейная корреляция

Выборочный коэффициент корреляции компонент X и Y двумерной случайной величиной (X, Y) выборочной совокупности объемом n рассчитывается по формуле

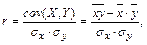
Определение 14. Статистическим распределением выборки называют перечень вариант x_i вариационного ряда и соответствующих им частот n_i (сумма всех частот равна объему выборки n) или относительных частот w_i (сумма всех относительных частот равна единице).

Определение 15. Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), …, (x_k, n_k).

Определение 16. Полигоном относительных частот (частости) называют ломаную, отрезки которой соединяют точки

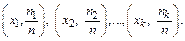
Числовые характеристики