Относительная продольная деформация определяется по формуле

$$

$

$

$

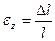
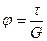
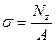
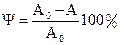
$$$433. Нормальное напряжение – это напряжение, которое…

$$ действует по нормали к сечению

$ не превышает допускаемого

$ действует в плоскости поперечного сечения

$ направлено под углом 45 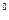к сечению

Поперечным называется сечение бруса

$$перпендикулярное к оси бруса

$ в заделке

$ наклонное к оси бруса под углом 45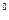

$ параллельное к оси бруса

$$$435. Изотропными называются материалы, свойства которых в различных направлениях…

$$ одинаковы

$ различны

$ зависят от температуры

$ не зависят от температуры

Растяжением-сжатием называется такой вид нагружения бруса, при котором в его поперечных сечениях возникают

$$ продольные силы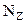

$ поперечные силы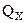

$ перерезывающие силы

$ изгибающие моменты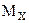

Тело, длина которого намного больше его поперечных размеров называется

$$ брус (стержень)

$ массив

$ пластина

$ оболочка

$$$438. Тело, толщина которого намного меньше двух его размеров, называется:

$$ пластина

$ массив

$ брус

$ стержень

Тело, у которого все три измерения имеют один порядок, называется

$$ массив

$ брус

$ оболочка

$ пластина

Тело, ограниченное криволинейными поверхностями и один размер которого намного меньше, чем два других, называется

$$ оболочка

$ пластина

$ брус

$ массив

$$$441. Анизотропными называются материалы, свойства которых в различных направлениях…

$$ различны

$ одинаковы

$ постоянны

$ зависят от температуры

Свойство тел после снятия внешней нагрузки полностью восстанавливать свои первоначальные размеры и форму, называется

$$ упругость

$пластичность

$ формообразование

$ формование

Свойство материала приобретать под действием внешней нагрузки необратимые, остаточные деформации, называется

$$ пластичность

$ упругость

$ стабилизация

$ релаксация

В рамках рассматриваемого тела материал полностью, без пустот и зазоров, заполняет весь отведенный ему объем. Это гипотеза

$$ сплошности

$ однородности

$ о естественно ненапряженном состоянии тела

$ прямых нормалей

Свойства материала не зависят от величины выделенного из тела объема. Это гипотеза

$$однородности

$ сплошности

$ плоских сечений

$ прямых нормалей

Продольную ось бруса принято обозначать

$

$

$

$$

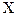
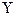
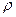
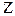
Статическим эквивалентом сил в поперечном сечении бруса при его центральном растяжении-сжатии является

$$ продольная сила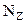

$ поперечная сила 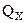$ перерезывающая сила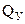

$ изгибающий момент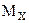

Если эпюра изгибающих моментов на участке балки (в правой системе координат) убывает, то поперечная сила на этом участке

$$ Отрицательна

$ Имеет скачок

$ Имеет максимум

$ Положительна