Поставим задачу: построить для произвольной булевой функции минимальные ДНФ. 3 страница
а) 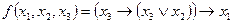 ;
;
б) 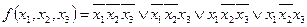 .
.
◄ а)Преобразуемформулу, используя равносильность 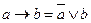 :
:
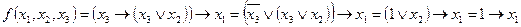 .
.
Поскольку на любом наборе 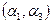
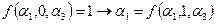 и на любом наборе
и на любом наборе 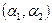
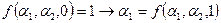 , то согласно определению
, то согласно определению  ,
, 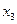 - фиктивные переменные. Переменная же
- фиктивные переменные. Переменная же  - существенная, т.к.
- существенная, т.к. 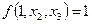 ,
, 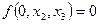 .
.
б)выполнить самостоятельно.►
Обратите внимание. Если функция реализована формулой, в которую некоторая переменная не входит, то эта переменная фиктивная. Обратное утверждение неверно. Действительно, в упражнении 14 а) мы рассмотрели функцию, реализованную формулой, содержащую переменные  ,
, 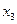 , однако эти переменные оказались фиктивными.
, однако эти переменные оказались фиктивными.
Упражнение 2.15. Выяснить, на скольких векторах 4-х мерного булева куба обращается в ноль функция: а) 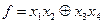 ; б)
; б) 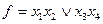 .
.
◄а)Функция 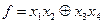 обращается в ноль, если
обращается в ноль, если 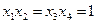 или
или 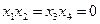 . Равенства
. Равенства 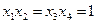 выполняются, только если все переменные равны единице. Равенства
выполняются, только если все переменные равны единице. Равенства 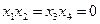 выполняются на таких наборах
выполняются на таких наборах 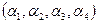 значений переменных
значений переменных 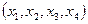 , у которых
, у которых 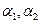 одновременно не равны единице и
одновременно не равны единице и 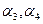 одновременно не равны единице. При построении конкретного булевого вектора
одновременно не равны единице. При построении конкретного булевого вектора 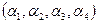 , отвечающего этим требованиям, будем сначала выбирать пару
, отвечающего этим требованиям, будем сначала выбирать пару 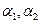 , а затем пару
, а затем пару 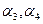 . Каждую из этих пар можно выбрать тремя способами (взять 0,0, или 0,1, или 1,0). Значит, согласно правилу произведения построить булев вектор, на котором оба слагаемых
. Каждую из этих пар можно выбрать тремя способами (взять 0,0, или 0,1, или 1,0). Значит, согласно правилу произведения построить булев вектор, на котором оба слагаемых 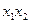 и
и 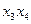 равны нулю, можно девятью способами.
равны нулю, можно девятью способами.
Таким образом, есть десять векторов, на которых функция 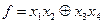 обращается в нуль.
обращается в нуль.
б)решить самостоятельно.►
Нормальные формы
2.2.1. Принцип двойственности
Определение. Функция, реализуемая формулой 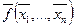 , называется двойственной к функции
, называется двойственной к функции 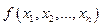 .
.
Функцию, двойственную к  , обозначают
, обозначают 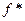 , т.е.
, т.е. 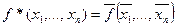 .
.
Упражнение 2.16.Используя определение, найти двойственные функции для дизъюнкции, конъюнкции и функций одной переменной.
◄ Пусть 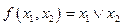 . Тогда
. Тогда 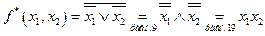 .
.
Пусть 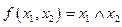 . Тогда
. Тогда 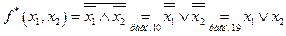 .
.
Пусть 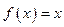 . Тогда
. Тогда 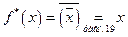 .
.
Пусть 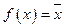 . Тогда
. Тогда 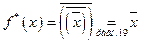 .
.
Пусть 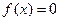 . Тогда
. Тогда 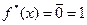 .
.
Пусть 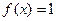 . Тогда
. Тогда 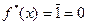 .►
.►
Утверждение. Для любой функции  выполняется равенство
выполняется равенство 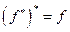 .
.
◄ 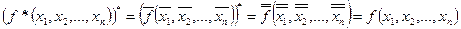 .►
.►
Обсудим, как найти двойственную функцию, если сама функция задана таблицей или вектором значений. Рассмотрим таблицы истинности для произвольной функции двух переменных 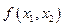 , а также двойственной к ней функции
, а также двойственной к ней функции 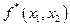 :
:
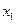 | 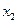 | 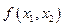 | 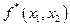 |
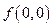 | 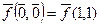 | ||
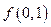 | 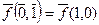 | ||
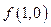 | 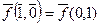 | ||
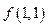 | 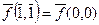 |
Нетрудно заметить, что столбец значений функции 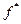 можно получить из столбца значений функции
можно получить из столбца значений функции  , если действовать по следующему алгоритму:
, если действовать по следующему алгоритму:
1. столбец значений функции переписать в обратном порядке (т.е. число, стоящее в первой строке, записать в последнюю строку; число, стоящее во второй строке - в предпоследнюю строку и т.д.);
2. в получившемся в результате выполнения пункта 1 столбце значений каждое число заменить его отрицанием (0 заменить 1 и 1 заменить 0).
Аналогичного алгоритма для получения двойственной функции можно придерживаться и в случае любого числа аргументов.
Упражнение 2.17.Найти функции, двойственные данным:
а) 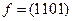 ; б)
; б)  ;
;
в) 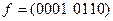 ; г)
; г) 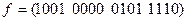 .
.
◄ а) 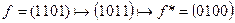 .
.
б) 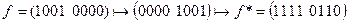 .
.
в)и г) решите самостоятельно.►
Упражнение 2.18.Найти функции, двойственные данным:
а) 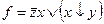 ; б)
; б) 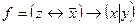 .
.
◄ а) Вначале зададим функцию таблицей:
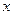 |  | 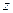 | 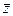 | 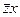 |  | 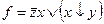 |
Далее: 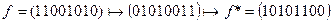 .
.
б)решите самостоятельно.►
Итак, если функция  задана формулой, то, чтобы найти двойственную к
задана формулой, то, чтобы найти двойственную к  функцию, можно вначале задать функцию
функцию, можно вначале задать функцию  вектором значений, а затем по вектору значений
вектором значений, а затем по вектору значений  выписать вектор значений
выписать вектор значений 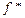 . Но можно действовать и по другому: строить формулу, реализующую
. Но можно действовать и по другому: строить формулу, реализующую 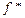 , непосредственно по формуле, реализующей
, непосредственно по формуле, реализующей  . Алгоритм такого построения дает принцип двойственности.
. Алгоритм такого построения дает принцип двойственности.
Принцип двойственности. Если формула 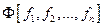 реализует функцию
реализует функцию 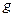 , то формула, полученная из нее заменой символов функций
, то формула, полученная из нее заменой символов функций 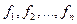 на символы двойственных к ним функций
на символы двойственных к ним функций 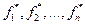 , реализует функцию
, реализует функцию 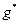 , двойственную к функции
, двойственную к функции 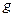 (эту формулу будем называть двойственной к
(эту формулу будем называть двойственной к 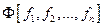 и обозначать
и обозначать 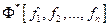 ).
).
Принцип двойственности удобен при нахождении двойственных функций в случае, если функция задана формулой. Особенно часто используют его следствие:
Поскольку 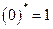 ,
, 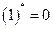 ,
, 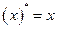 ,
, 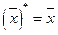 ,
, 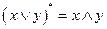 ,
, 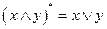 , то для получения формулы, двойственной к формуле
, то для получения формулы, двойственной к формуле 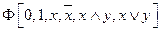 , нужно в формуле
, нужно в формуле  заменить 0 на 1, 1 на 0, связку
заменить 0 на 1, 1 на 0, связку 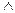 на связку
на связку 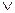 , связку
, связку 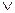 на связку
на связку 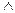 .
.
Упражнение 2.19. Реализовать формулами функции, двойственные данным:
а) 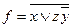 ; б)
; б) 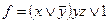 ; в)
; в) 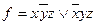 ; г)
; г) 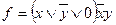 .
.
◄ а) 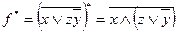 .
.
Обратите внимание на следующее обстоятельство. В записи формулы, реализующей  , конъюнкция, согласно соглашению о краткой записи формул, в скобки не взята. Записывая двойственную формулу, мы меняем конъюнкцию на дизъюнкцию. Но связка «
, конъюнкция, согласно соглашению о краткой записи формул, в скобки не взята. Записывая двойственную формулу, мы меняем конъюнкцию на дизъюнкцию. Но связка « 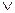 » имеет меньший приоритет выполнения, чем «
» имеет меньший приоритет выполнения, чем « 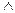 », поэтому, чтобы двойственная формула сохранила структуру исходной формулы, при переходе от конъюнкции к дизъюнкции нужно взять дизъюнкцию в скобки. В то же время при переходе от дизъюнкции к конъюнкции скобки можно опустить.
», поэтому, чтобы двойственная формула сохранила структуру исходной формулы, при переходе от конъюнкции к дизъюнкции нужно взять дизъюнкцию в скобки. В то же время при переходе от дизъюнкции к конъюнкции скобки можно опустить.
б) 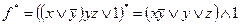 .
.
в)и г) решите самостоятельно.►
2.2.2. Реализация булевых функций в виде СДНФ и СКНФ.
Мы научились задавать вектором значений функцию, реализованную формулой. Для приложений важно уметь решать и обратную задачу, т.е. уметь реализовывать формулой функцию, заданную вектором значений. У этой задачи не одно решение, поскольку существуют семейства равносильных между собой формул.
Начнем с того, что научимся реализовывать функцию в виде совершенной дизъюнктивной нормальной формы.
Введем обозначение: 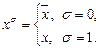
Теорема (о реализации функции в виде СДНФ). Если  , то она может быть реализована формулой
, то она может быть реализована формулой
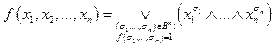 . (*)
. (*)
Формулу (*) называют совершенной дизъюнктивной нормальной формой или, сокращенно,СДНФ.
Согласно (*), чтобы записать СДНФ функции, нужно действовать так:
1) выбрать в таблице истинности функции все наборы значений переменных, на которых функция равна 1;
2) для каждого такого набора записать конъюнкцию, в которую войдут все переменные, причем, если значение переменной на данном наборе равно 0, то она войдет в конъюнкцию со знаком отрицания, а если – 1, то без знака отрицания;
3) записать дизъюнкцию всех выписанных в п. 2 конъюнкций.
Упражнение 2.20.Реализоватьфункции в виде СДНФ:
а) 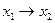 ; б)
; б) 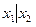 ; в)
; в) 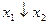 ; г)
; г) 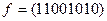 ; д)
; д) 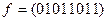 .
.
◄ а) – в) Зададим функции таблично и выпишем для них СДНФ.
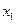 | 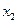 | 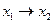 | 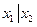 | 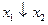 |
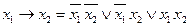 ;
;
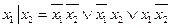 ;
;
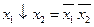 .
.
г) Таблица истинности функции 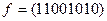 приведена в упражнении 2.18 б. Запишем СДНФ:
приведена в упражнении 2.18 б. Запишем СДНФ: 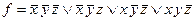 .
.
д)решите самостоятельно. ►
Рассмотрим еще один способ реализации функции формулой.
Теорема (о реализации функции в виде СКНФ). Если  , то она может быть реализована формулой
, то она может быть реализована формулой
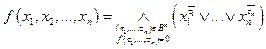 . (**)
. (**)
Формулу (**), называют совершенной конъюнктивной нормальной формой или, сокращенно,СКНФ.
Согласно (**), чтобы записать СКНФ функции, нужно действовать так:
1) выбрать в ее таблице истинности все наборы значений переменных, на которых функция равна 0;
2) для каждого такого набора записать дизъюнкцию, в которую войдут все переменные, причем, если значение переменной на данном наборе равно 1, то она войдет в дизъюнкцию со знаком отрицания, а если – 1, то без знака отрицания;
3) записать конъюнкцию всех выписанных в п. 2 дизъюнкций.
Упражнение 2.21.Реализоватьфункции в виде СКНФ:
а) 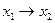 ; б)
; б) 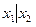 ; в)
; в) 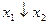 ; г)
; г) 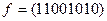 ; д)
; д) 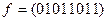 .
.
◄ а) – г) Опираясь на таблицы истинности функций (они приведены в упражнениях 20 и 18), запишем:
а) 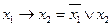 ;
;
б) 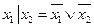 ;
;
в) 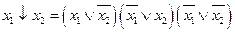 ;
;
г) 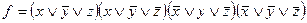 .
.
д) решите самостоятельно. ►
§ 2.3. Минимизация булевых функций в классе ДНФ
Пусть задан алфавит переменных 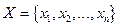 .
.
Определение. Формулу вида 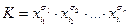 (
( 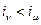 при
при 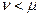 ,
, 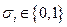 ) называют элементарной конъюнкцией ранга r над множеством X. Константа 1 рассматривается как элементарная конъюнкция ранга 0.
) называют элементарной конъюнкцией ранга r над множеством X. Константа 1 рассматривается как элементарная конъюнкция ранга 0.
Например, формула 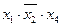 - элементарная конъюнкция ранга 3 над множеством
- элементарная конъюнкция ранга 3 над множеством 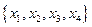 ; в то время как формула
; в то время как формула 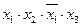 элементарной конъюнкцией не является.
элементарной конъюнкцией не является.
Упражнение 2.22. а)Перечислите все элементарные конъюнкции ранга 3 над множеством 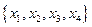 , обращающиеся в единицу на наборе
, обращающиеся в единицу на наборе 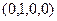 .
.
б)Перечислите все элементарные конъюнкции над множеством 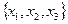 , обращающиеся в единицу на наборе
, обращающиеся в единицу на наборе 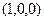 .
.
◄ а) 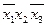 ,
, 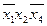 ,
, 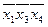 ,
, 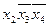 ; б)
; б) 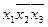 ,
, 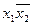 ,
, 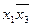 ,
, 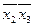 ,
, 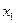 ,
, 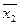 ,
, 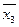 ,1.►
,1.►
Определение. Формулу вида 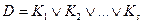 (
( 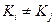 при
при 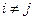 ), где через
), где через 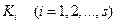 обозначены элементарные конъюнкции над множеством X, называют дизъюнктивной нормальной формой (ДНФ) над множеством X. Сумма рангов конъюнкций, входящих в ДНФ, называется сложностью ДНФ.
обозначены элементарные конъюнкции над множеством X, называют дизъюнктивной нормальной формой (ДНФ) над множеством X. Сумма рангов конъюнкций, входящих в ДНФ, называется сложностью ДНФ.
Например, 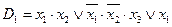 - ДНФ сложности 6;
- ДНФ сложности 6; 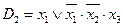 - ДНФ сложности 4;
- ДНФ сложности 4; 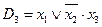 - ДНФ сложности 3 над множеством
- ДНФ сложности 3 над множеством 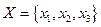 .
.
Заметим, что формулы 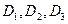 равносильны и, следовательно, реализуют одну и ту же функцию h. Делаем вывод: функция может быть реализована в виде ДНФ не единственным образом, причем ДНФ, реализующие функцию, могут иметь различную сложность.
равносильны и, следовательно, реализуют одну и ту же функцию h. Делаем вывод: функция может быть реализована в виде ДНФ не единственным образом, причем ДНФ, реализующие функцию, могут иметь различную сложность.
Определение. ДНФ, имеющая по сравнению с другими ДНФ, реализующими данную функцию, наименьшую сложность, называется минимальной дизъюнктивной нормальной формой данной функции.
Так, для функции h (см. выше), реализуемой дизъюнктивными нормальными формами 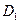 ,
, 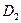 ,
, 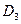 дизъюнктивная нормальная форма
дизъюнктивная нормальная форма 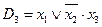 является минимальной, поскольку h зависит от переменных
является минимальной, поскольку h зависит от переменных  существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв.
существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв.
Поставим задачу: построить для произвольной булевой функции минимальные ДНФ.
Заметим, что у этой задачи существует тривиальное решение. Дадим его пошаговое описание.
1. Строим все ДНФ над множеством 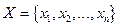 . Их
. Их 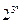 . Действительно, число различных элементарных конъюнкций равно
. Действительно, число различных элементарных конъюнкций равно 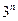 , так как для каждой переменной
, так как для каждой переменной 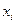 имеется три возможности: присутствовать в конъюнкции, присутствовать с отрицанием и отсутствовать («пустой» конъюнкции сопоставлена константа 1). Каждая из конъюнкций, в свою очередь, может либо входить, либо не входить в ДНФ.
имеется три возможности: присутствовать в конъюнкции, присутствовать с отрицанием и отсутствовать («пустой» конъюнкции сопоставлена константа 1). Каждая из конъюнкций, в свою очередь, может либо входить, либо не входить в ДНФ.
2. Отбираем из построенных ДНФ те, которые реализуют функцию  .
.
3. Для отобранных ДНФ определяем сложности; ДНФ наименьшей сложности и есть искомые минимальные ДНФ функции  .
.
