Задания для самостоятельной работы. 1. Вычислите , если
1. Вычислите  , если
, если  .
.
2. Докажите, что если 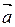 ||
|| 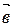 , то
, то 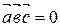 .
.
3. Выясните, какой является тройка векторов  ,
,  ,
,  (левой или правой).
(левой или правой).
4. Докажите, что векторы 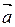 ,
, 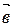 ,
, 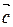 , удовлетворяющие условию
, удовлетворяющие условию 
 ,компланарны.
,компланарны.
5. Найдите объем треугольной призмы АВСА1В1С1, если  ,
,  ,
,  .
.
6. Найдите объем тетраэдра ABCD, если  ,
,  ,
,  .
.
Метод координат
На плоскости и в пространстве
Лекция 7
Аффинная и прямоугольная декартова
Системы координат
Понятие аффинной и прямоугольной декартовой
Систем координат
 Четверка, состоящая из точки О и базиса
Четверка, состоящая из точки О и базиса 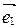 ,
, 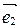 ,
, 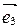 в пространстве, называется аффинной системой координат в пространстве и обозначается
в пространстве, называется аффинной системой координат в пространстве и обозначается  или
или  (рис. 30).
(рис. 30).
Точка О называется началом координат, векторы 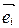 ,
, 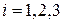 , - координатными векторами:
, - координатными векторами: 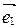 - первый координатный вектор,
- первый координатный вектор, 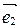 - второй,
- второй,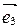 - третий.
- третий.
Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точку О, называются координатными осями:
 - ось абсцисс;
- ось абсцисс;
 - ось ординат;
- ось ординат;
 - ось аппликат (рис. 31).
- ось аппликат (рис. 31).
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, Оz.
Плоскости, определяемые осями Ох и Оу, Оу и Оz, Ох и Оz, называются координатными плоскостями и обозначаются Оху, Оуz, Oxz, а систему координат  иногда обозначают Oxyz.
иногда обозначают Oxyz.
 Пусть
Пусть  - аффинная система координат, М – произвольная точка пространства. Вектор
- аффинная система координат, М – произвольная точка пространства. Вектор  называется радиус-вектором точки М относительно точки О(рис. 32).
называется радиус-вектором точки М относительно точки О(рис. 32).
Понятие координат точки вводится на основе понятия координат вектора.
Координатами точки М в системе координат называются координаты ее радиус-вектора
называются координаты ее радиус-вектора  в базисе
в базисе 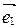 ,
, 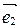 ,
, 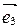 .
.
Обозначение  или просто М(х;у;z): х – абсцисса точки М, у – ордината, z – аппликата.
или просто М(х;у;z): х – абсцисса точки М, у – ордината, z – аппликата.
Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у;z) действительных чисел.
Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у;z).
1) Если z=0, то М(х;у;0) Þ  Þ
Þ  . Верно и обратное:
. Верно и обратное:  Þ z=0.
Þ z=0.
2) Докажите самостоятельно, что если у=0, то  , и наоборот, если
, и наоборот, если  , то у=0.
, то у=0.
3) Докажите самостоятельно, что если х=0, то  , и наоборот, если
, и наоборот, если  , то х=0.
, то х=0.
4) Если z=0 и у=0, то  и
и  Þ
Þ  Þ
Þ  . Верно и обратное:
. Верно и обратное:  Þ z=0 и у=0.
Þ z=0 и у=0.
Докажите самостоятельно, что:
5) Если х=0 и у=0, то  и наоборот, если
и наоборот, если  , то х=0 и у=0.
, то х=0 и у=0.
6) Если х=0 и z=0, то  и наоборот, если
и наоборот, если  , то х=0 и z=0.
, то х=0 и z=0.
7) Так как  , то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат
, то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат  .
.
Чтобы построить точку М(х;у;z) по ее координатам в системе координат  , надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 33. Ломаная ОМ1М2М называется координатной ломаной точки М.
, надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 33. Ломаная ОМ1М2М называется координатной ломаной точки М.
 Система координат называется прямоугольной декартовой, если ее базис является ортонормированным. Обозначение прямоугольной декартовой системы координат:
Система координат называется прямоугольной декартовой, если ее базис является ортонормированным. Обозначение прямоугольной декартовой системы координат:  или
или  , где
, где 
 ,
,  ,
,  и
и  .
.
Прямоугольная декартова система координат является частным случаем аффинной.
Замечание. На плоскости аффинная система координат состоит из точки О (начала координат) и двух базисных векторов 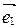 и
и 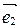 (координатных векторов) (рис. 34). Поэтому в системе координат на плоскости любая точка имеет две координаты
(координатных векторов) (рис. 34). Поэтому в системе координат на плоскости любая точка имеет две координаты  . Прямоугольная декартова система координат на плоскости изображена на рис. 35.
. Прямоугольная декартова система координат на плоскости изображена на рис. 35.
 |
