Разложение определителей

Выберем в квадратной матрице 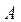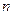-го порядка строки с номерами 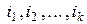и столбцы с номерами 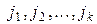, где .

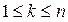Определение. Детерминант квадратной матрицы порядка k, образованной элементами, стоящими на пересечении строк 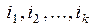и столбцов 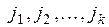, называется минором k-го порядка иобозначается .

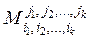Определение. Детерминант квадратной матрицы порядка 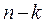, образованной элементами, остающимися после вычеркивания строк 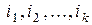и столбцов 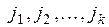, называется дополнительным минором к минору 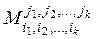, и обозначается .

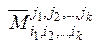Выберем в матрице 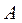i-ю строку и j-й столбец, на пересечении которых расположен элемент 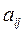. Удалим из 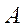выбранные строку и столбец, рассмотрим квадратную матрицу 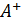размера .

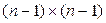Определение. Детерминант матрицы 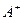называется дополнительным минором 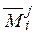элемента .

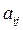Сгруппируем в определении детерминанта матрицы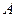

,

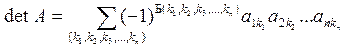все 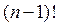слагаемых, содержащих элемент 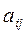, и вынесем его за скобки. Получим выражение вида

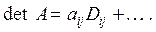
Определение. Число 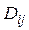называется алгебраическим дополнением элемента .

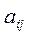Замечание. По определению детерминанта имеют место равенства

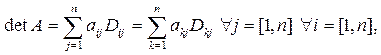(12.1)

которые можно использовать для вычисления определителей квадратных матриц, находя значения алгебраических дополнений при помощи соотношений, которые устанавливает следующая теорема

Теорема 12.4Справедливы равенства .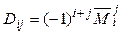

Доказательство.

1°. По определению детерминанта

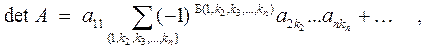
то есть 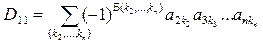, поскольку очевидно, что 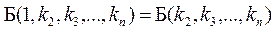, но тогда выражение для 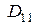совпадает с формулой определителя матрицы порядка 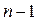, получаемой из 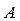вычеркиванием первого столбца и первой строки. Следовательно, .

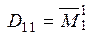2°. Построим новую матрицу, 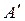переместив элемент 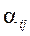матрицы 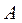в ее левый верхний угол, переставив i-ю строку на первое место, для чего потребуется 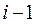перестановок, и переставим на первое место j-й столбец, что потребует 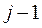перестановок. Тогда определитель перестроенной матрицы 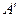равен

.

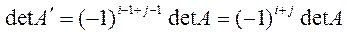Согласно линейному свойству определителя данное соотношение будет также выполняться и для каждого из его слагаемых, а значит, в силу формул (12.1) и для каждого алгебраического дополнения 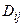. Поэтому справедливо равенство

.

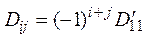3°. Наконец, очевидно, что значение дополнительного к 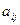минора не зависит от положения 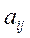в матрице 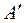, и потому .

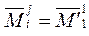4°. Учитывая полученные соотношения

,

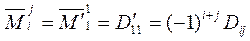приходим к равенству .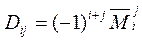

Теорема доказана.

Следствие. Разложение определителя по i-му столбцу имеет вид

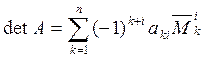
или

.

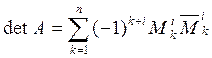Теорема 12.5Для любой квадратной матрицы 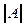имеет место равенство

,

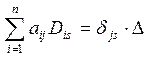где 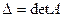и

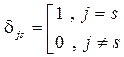–символ Кронекера

Доказательство.

По определению алгебраического дополнения имеем

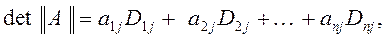
то есть утверждение теоремы для случая 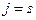справедливо.

Пусть теперь 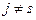. Тогда выражение

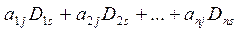
можно рассматривать как разложение по s-му столбцу определителя матрицы, у которой s-й столбец совпадает с j-м столбцом. Но такой определитель равен нулю.

Теорема доказана.

Следствие. Если квадратная матрица 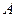невырожденна, то элементами ее обратной матрицы 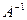являются числа .

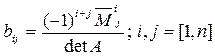Правило Крамера

Рассмотрим систему n линейных уравнений с n неизвестными:

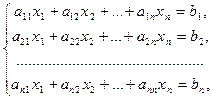(12.2)

Или

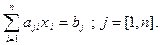(12.3)

Или же в матричной форме

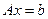, (12.4)

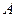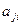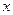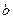где квадратная матрица имеет компоненты , а столбцы и – соответственно компоненты 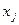и .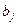

Определение. Упорядоченный набор чисел 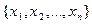будем называть решением системы линейных уравнений, если при подстановке этих чисел в каждое из уравнений системы мы получаем тождество.

Теорема 12.5 (правило Крамера)Для того чтобы система линейных уравнений (12.2) имела единственное решение, необходимо и достаточно, чтобы 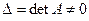и в этом случае решение данной системы будет иметь вид

,

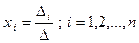где 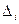– определитель матрицы, получаемой из матрицы 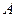заменой ее i-го столбца на столбец свободных членов :

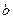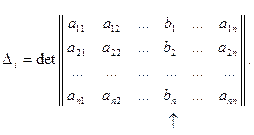
i-й столбец

Ранг матрицы

Рассмотрим матрицу 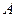размера 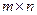. Пусть 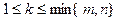. Выберем k фиксированных столбцов и строк, на пересечении которых стоит матрица минора порядка k.

Пусть при данном k все миноры k-го порядка равны нулю, тогда будут равны нулю и все миноры порядка выше, чем k, поскольку каждый минор 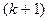-го порядка представим в виде линейной комбинации миноров порядка k.

Определение. Наивысший из порядков, отличных от нуля миноров матрицы 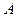, называется рангом матрицы и обозначается .

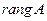Определение. Любой ненулевой минор матрицы, порядок которого равен ее рангу, называется базисным минором.

Определение. Столбцы (строки) матрицы, входящие в матрицу базисного минора, называются базисными.

Рассмотрим n m-компонентных столбцов вида:

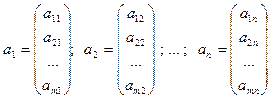
и столбцы

.

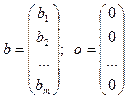Поскольку для столбцов (как частного случая матриц) определены операции сравнения, сложения и умножения на число, то будем говорить, что столбец 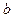есть линейная комбинация столбцов 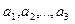, если существуют числа 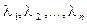, такие, что

.

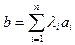Теорема 12.6Всякий столбец (строка) матрицы есть линейная комбинация базисных столбцов (строк) этой матрицы.

Доказательство.

1°. Пусть ранг матрицы равен 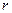. Без ограничения общности можно считать, что матрица базисного минора расположена в левом верхнем углу матрицы .

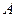Окаймим матрицу базисного минора фрагментами i-й строки и j-го столбца и рассмотрим определитель построенной матрицы

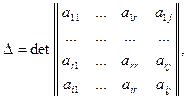
который равен нулю как минор порядка 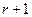в матрице ранга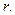

2°. Разложив определитель D по последней строке, получим

,

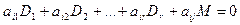где 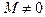– базисный минор, а 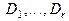– некоторые алгебраические дополнения, не зависящие от i. Следовательно, 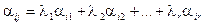, где

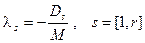и .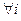

Теорема доказана.

Определение. Столбцы 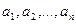будем называть линейно зависимыми, если существуют не равные нулю одновременно числа 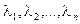, такие, что .

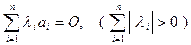Лемма 12.1 Для того чтобы столбцы (строки) матрицы были линейно зависимыми, необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.

Лемма 12.2 Если один из столбцов матрицы есть линейная комбинация некоторого подмножества остальных, то столбцы этой матрицы линейно зависимы.

Доказательство.

По лемме 6.5.1 можно утверждать, что среди столбцов матрицы есть подмножество линейно зависимых. Допустим, что линейно зависимыми являются первые 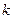столбцов, то есть для них существует нетривиальная линейная комбинация, равная нулевому столбцу:

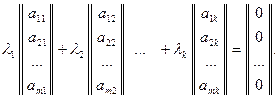
Тогда очевидно, что нетривиальная линейная комбинация всех столбцов этой матрицы вида

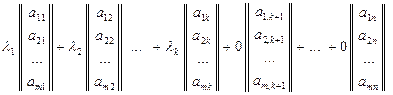
будет также равна нулевому столбцу.

Лемма доказана.

Теорема 12.7Для того чтобы определитель был равен нулю, необходимо и достаточно, чтобы его столбцы (строки) были линейно зависимыми.

Доказательство необходимости.

Пусть определитель равен нулю, тогда ранг его матрицы меньше n. По теореме о базисном миноре всякий столбец есть линейная комбинация базисных столбцов и тогда по лемме 12.2 столбцы матрицы линейно зависимы.

Доказательство достаточности:

Пусть столбцы матрицы линейно зависимы. По лемме 12.1 один из столбцов есть линейная комбинация остальных.

Пусть этот столбец последний, то есть 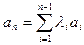. Умножим последовательно (для 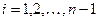) i-й столбец на число 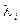и сложим все их. Вычитание этой суммы из столбца 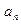не изменит величины определителя, но поскольку при этом мы получим нулевой столбец, то определитель равен нулю.

Теорема доказана.

Теорема 12.8 (о ранге матрицы)Максимальное число линейно независимых столбцов матрицы равно максимальному числу линейно независимых строк матрицы и равно рангу матрицы.

Доказательство.

1°. Если ранг матрицы нулевой, то все ее элементы нулевые и среди них нет линейно независимых.

Пусть ранг матрицы равен 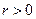. Рассмотрим матрицу, составленную из r базисных столбцов матрицы. Она имеет ненулевой минор r-го порядка и, следовательно, ее столбцы линейно независимы.

2°. Выберем 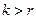столбцов матрицы и покажем, что эти столбцы линейно зависимы. Построим из выбранных столбцов матрицу 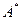. Ее ранг 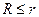, поскольку 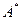является частью матрицы 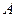. Следовательно, 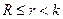и в матрице 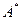есть, по крайней мере, один небазисный столбец, и тогда столбцы матрицы 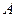линейно зависимы по лемме 12.2.

Теорема доказана.

12.6 Системы m линейных уравнений с n неизвестными

Рассмотрим систему m линейных уравнений с n неизвестными вида:

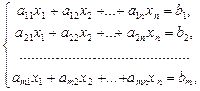
Или

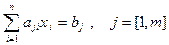(12.5)

или же в матричной форме

,

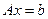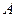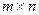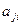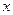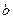где матрица размера имеет компоненты , а столбцы и соответственно компоненты 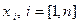, и .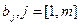

Определение. Упорядоченный набор чисел 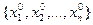будем называть частным решением системы линейных уравнений(12.5), если при подстановке этих чисел в систему мы получаем верные равенства. Частное решение системы линейных уравнений может также быть записано в виде столбца

.

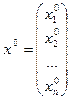Совокупность всех частных решений системы линейных уравнений(12.5) назовем общим решением системы (12.5).

Определение. Если система (12.5) имеет хотя бы одно частное решение, то она называется совместной, в противном случае – несовместной системой уравнений.

Определение. Матрица 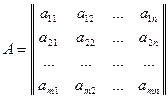называется основной матрицей системы (12.5), а матрица

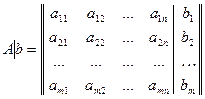
– расширенной матрицей этой системы.

Определение. Система (12.5) называется однородной, если 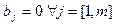, в противном случае - неоднородной системой уравнений.

Теорема 12.9 (Кронекера-Капелли)Для того чтобы система (12.5) была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной.

Доказательство необходимости.

Пусть существует решение системы (12.5) 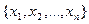, тогда эту систему можно представить в виде следующего равенства:

,

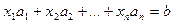где .

Поскольку в этом случае столбец свободных членов есть линейная комбинация столбцов, образующих основную матрицу, то число линейно независимых столбцов основной и расширенной матриц будет одинаковым. Следовательно, по теореме о ранге матрицы .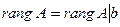

Доказательство достаточности.

Пусть ранг основной матрицы равен рангу расширенной матрицы и равен r. Без ограничения общности предположим, что базисный минор расположен в левом верхнем углу расширенной матрицы, но тогда по теореме о базисном миноре имеет место равенство 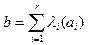, которое можно переписать в виде

.

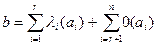Однако последнее означает, что система (12.5) имеет решение 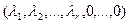, то есть она совместна.

Теорема доказана.