Определение векторного пространства
Определение. Пусть имеется множество 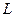 , на котором введена бинарная операция
, на котором введена бинарная операция 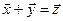 (отображение
(отображение 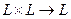 ). Пусть также определена операция умножения элементов множества
). Пусть также определена операция умножения элементов множества 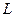 на элементы, принадлежащие полю
на элементы, принадлежащие полю 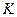 ,
, 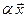 , где
, где 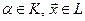 (т.е. отображение
(т.е. отображение 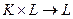 ). Множество
). Множество 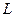 называется векторным пространством (или линейным пространством) над полем
называется векторным пространством (или линейным пространством) над полем 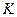 , если выполняются следующие условия:
, если выполняются следующие условия:
1) 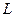 - абелева группа относительно введенной бинарной операции
- абелева группа относительно введенной бинарной операции 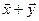 , единичный элемент этой группы будем обозначать
, единичный элемент этой группы будем обозначать 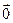 и называть нулевым вектором;
и называть нулевым вектором;
2) 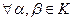 и
и 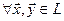 справедливы равенства
справедливы равенства 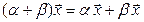 и
и 
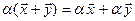 ;
;
3) 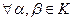 и
и 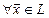 имеет место равенство
имеет место равенство 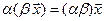 ;
;
4) 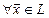 выполняется равенство
выполняется равенство 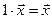 , где
, где 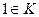 .
.
Элементы векторного пространства 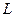 называются векторами.
называются векторами.
Определение. Пусть некоторое подмножество 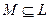 обладает следующими свойствами: а) если
обладает следующими свойствами: а) если 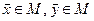 , то и
, то и 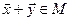 ; б) если
; б) если 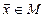 , то и
, то и 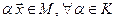 . Подмножество
. Подмножество 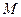 , являющееся векторным пространством, называется подпространством пространства
, являющееся векторным пространством, называется подпространством пространства 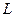 . Нулевой вектор пространства
. Нулевой вектор пространства 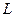 и само пространство
и само пространство 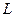 называют тривиальными подпространствами пространства
называют тривиальными подпространствами пространства 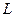 . Все остальные подпространства пространства
. Все остальные подпространства пространства 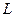 называются нетривиальными.
называются нетривиальными.
Определение. Пусть 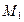 и
и 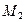 - два подпространства одного и того же векторного пространства
- два подпространства одного и того же векторного пространства 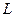 . Множество всех векторов
. Множество всех векторов 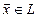 , принадлежащих одновременно подпространствам
, принадлежащих одновременно подпространствам 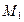 и
и 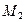 , называется их пересечением. Множество всех векторов вида
, называется их пересечением. Множество всех векторов вида 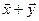 , где
, где 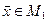 и
и 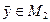 , носит название суммы подпространств
, носит название суммы подпространств 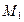 и
и 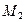 . Как пересечение, так и сумма подпространств являются, в свою очередь, векторными пространствами - подпространствами пространства
. Как пересечение, так и сумма подпространств являются, в свою очередь, векторными пространствами - подпространствами пространства 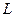 .
.
Определение. Говорят, что пространство 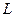 является прямой суммой своих подпространств
является прямой суммой своих подпространств 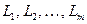 , если: а)
, если: а) 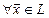 существует разложение
существует разложение 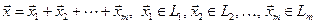 ; б) это разложение единственно. В этом случае будем писать
; б) это разложение единственно. В этом случае будем писать 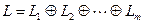 .
.
2. Линейная оболочка системы векторов, линейно независимые вектора, базис векторного пространства, координаты вектора, размерность пространства, преобразования базисов и координат.
Пусть 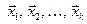 - некоторые векторы пространства
- некоторые векторы пространства 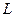 . Полное множество векторов вида
. Полное множество векторов вида 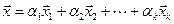 , где
, где 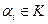 , называется линейной оболочкой системы векторов
, называется линейной оболочкой системы векторов 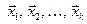 . Линейная оболочка векторов является векторным пространством (говорят, что векторное пространство «натянуто» на векторы
. Линейная оболочка векторов является векторным пространством (говорят, что векторное пространство «натянуто» на векторы 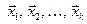 ).
).
Рассмотрим подпространство 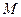 векторного пространства
векторного пространства 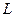 . Назовем вектор
. Назовем вектор 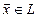 сравнимым с вектором
сравнимым с вектором 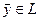 (точнее, сравнимым относительно
(точнее, сравнимым относительно 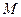 ), если
), если 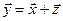 , где
, где 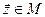 . Отношение сравнения является отношением эквивалентности и позволяет разбить векторное пространство
. Отношение сравнения является отношением эквивалентности и позволяет разбить векторное пространство 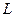 на взаимно непересекающиеся классы эквивалентности
на взаимно непересекающиеся классы эквивалентности 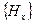 . Здесь
. Здесь 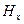 - совокупность всех векторов пространства
- совокупность всех векторов пространства 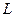 , сравнимых с вектором
, сравнимых с вектором 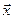 . Определенное таким образом множество классов эквивалентности
. Определенное таким образом множество классов эквивалентности 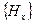 обозначим
обозначим 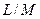 . Введем на множестве
. Введем на множестве 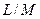 бинарную операцию
бинарную операцию 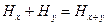 и правило умножение элементов этого множества на числа из поля
и правило умножение элементов этого множества на числа из поля 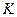
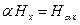 . Введенные операции превращают множество
. Введенные операции превращают множество 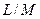 в векторное пространство.
в векторное пространство.
Определение. Векторное пространство 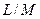 называется факторпространством пространства
называется факторпространством пространства 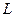 по подпространству
по подпространству 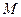 .
.
Заметим, что если 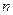 - размерность пространства
- размерность пространства 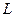 , а
, а 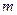 - размерность подпространства
- размерность подпространства 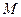 , то размерность факторпространства
, то размерность факторпространства 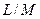 равна
равна 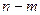 .
.
