Метод половинного деления
Для нахождения корня уравнения (1), принадлежащего отрезку [a, b], делим этот отрезок пополам. Если f 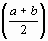 = 0 , то x =
= 0 , то x = 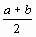 является корнем уравнения. Если f
является корнем уравнения. Если f 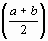 не равно 0 (что, практически, наиболее вероятно), то выбираем ту из половин
не равно 0 (что, практически, наиболее вероятно), то выбираем ту из половин 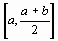 или
или 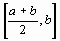 , на концах которой функция f(x)имеет противоположные знаки. Новый суженный отрезок [ а1, b1] снова делим пополам и производим те же самые действия.
, на концах которой функция f(x)имеет противоположные знаки. Новый суженный отрезок [ а1, b1] снова делим пополам и производим те же самые действия.
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.
Пример 3. Методом половинного деления уточнить корень уравнения
f(x) = x4 + 2 x3 - x - 1 = 0
лежащий на отрезке [ 0, 1] .
Последовательно имеем:
f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 - 0,5 - 1 = - 1,19;
f(0,75) = 0,32 + 0,84 - 0,75 - 1 = - 0,59;
f(0,875) = 0,59 + 1,34 - 0,88 - 1 = + 0,05;
f(0,8125) = 0,436 + 1,072 - 0,812 - 1 = - 0,304;
f(0,8438) = 0,507 + 1,202 - 0,844 - 1 = - 0,135;
f(0,8594) = 0,546 + 1,270 - 0,859 - 1 = - 0,043 и т. д.
Можно принять
x = 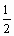 (0,859 + 0,875) = 0,867
(0,859 + 0,875) = 0,867
Метод хорд
В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения (1) принимаются значения х1, х2, ..., хn точек пересечения хорды АВ с осью абсцисс (Рисунок 3). Сначала запишем уравнение хорды AB:
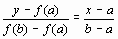 .
.
Для точки пересечения хорды AB с осью абсцисс (х = х1, y = 0) получим уравнение:
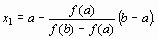
Пусть для определенности f'' (x)>0 при а 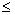 х
х 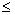 b (случай f'' (x)<0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2) f(b) < 0 (Рисунок 3, б).
b (случай f'' (x)<0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2) f(b) < 0 (Рисунок 3, б).
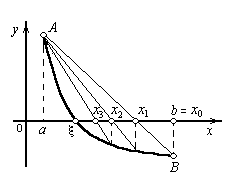
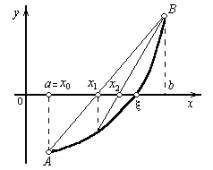
Рисунок 3, а, б.
В первом случае конец а неподвижен и последовательные приближения: x0 = b;
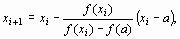 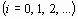 | (5) |
образуют ограниченную монотонно убывающую последовательность, причем
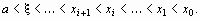
Во втором случае неподвижен конец b, а последовательные приближения: x0 = а;
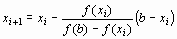 | (6) |
образуют ограниченную монотонно возрастающую последовательность, причем
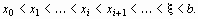
Обобщая эти результаты, заключаем:
- неподвижен тот конец, для которого знак функции f (х) совпадает со знаком ее второй производной f'' (х);
- последовательные приближения xn лежат по ту сторону корня x , где функция f (х) имеет знак, противоположный знаку ее второй производной f'' (х).
Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что
| xi - xi - 1|< e ,
где e - заданная предельная абсолютная погрешность.
Пример 4.Найти положительный корень уравнения
f(x) = x3 - 0,2 x2 - 0,2 х - 1,2 = 0
с точностью e = 0,01.
Прежде всего, отделяем корень. Так как
f (1) = -0,6 < 0 и f (2) = 5,6 > 0,
то искомый корень x лежит в интервале [1, 2]. Полученный интервал велик, поэтому разделим его пополам. Так как
f (1,5) = 1,425 > 0, то 1< x < 1,5.
Так как f'' (x) = 6 x - 0,4 > 0 при 1 < х < 1,5 и f (1,5) > 0, то воспользуемся формулой (5) для решения поставленной задачи:
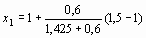 = 1,15;
= 1,15;
|x1- x0| = 0,15 > e ,
следовательно, продолжаем вычисления;
f (х1) = -0,173;
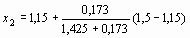 = 1,190;
= 1,190;
|x2- x1| = 0,04 > e ,
f (х2) = -0,036;
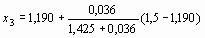 = 1,198;
= 1,198;
|x3- x2| = 0,008 < e .
Таким образом, можно принять x = 1,198 с точностью e = 0,01.
Заметим, что точный корень уравнения x = 1,2.
Методы приближенного решения уравнений вида f(x)=0
