Метод половинного деления

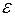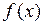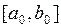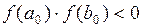Среди численных методов решения уравнения (2.1) наиболее простым в реализации является метод половинного деления. Он позволяет отыскивать корень уравнения (2.1) с любой заданной точностью и применим в том случае, если – непрерывна на и . Суть метода состоит в следующем.

Разбиваем 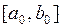пополам; среди двух получившихся отрезков выбираем тот, на концах которого 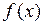принимает значения разных знаков. Получаем новый отрезок 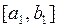, внутри которого находится точный корень уравнения. Данный процесс деления и выбора нового более узкого отрезка продолжаем до тех пор, пока на n-ом шаге длина полученного отрезка 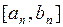не станет меньше 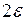. Тогда приближенный корень уравнения может быть найден по формуле

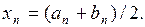(2.3)

При этом абсолютная погрешность найденного корня не превышает 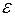, т. е. 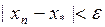. Может случиться, что на некотором шаге значение 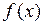в середине отрезка равно нулю. Тогда середина отрезка – точный корень уравнения (3.1).

Метод Ньютона

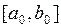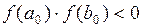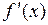Пусть корень уравнения (2.1) отделен на начальном отрезке , причем и и 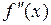отличны от нуля и знакопостоянны на этом отрезке. Ограничения на производные геометрически означают, что кривая 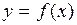не только идет в одном направлении, – все время вверх 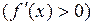или все время вниз 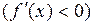, но к тому же строго выпукла вниз 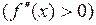или вверх .

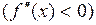Геометрический смысл метода Ньютона или иначе – метода касательных состоит в том, что к графику функции 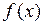проводится касательная в некоторой точке с абсциссой 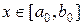, и вместо точки пересечения графика 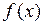с осью Ox ищется точка пересечения этой касательной с осью Ox (рис. 2.3).

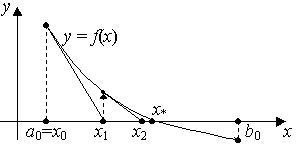
Рис. 2.3. Геометрическая иллюстрация метода Ньютона

В качестве начальной точки 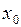выбирается тот из концов отрезка 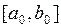, в котором функция 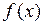и ее вторая производная имеют один и тот же знак

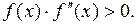(2.4)

Затем строят касательную к графику 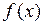в точке с абсциссой 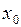, находят абсциссу 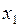точки пересечения касательной с осью Ox. Снова строят касательную к графику 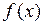уже в точке 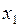и находят абсциссу 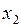точки пересечения новой касательной с осью Ox. Продолжая этот процесс, получают числовую последовательность

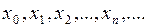(2.5)

Можно доказать [2], что при выполнении перечисленных в начале этого параг-рафа условий, последовательность (2.5) сходится к корню 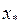уравнения (2.1).

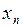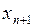Получим расчетную формулу для метода Ньютона. Пусть и – предыдущее и последующее приближения корня. Запишем уравнение касательной к графику функции в точке 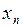: 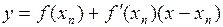. В уравнении положим 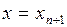, тогда 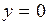(так как это точка пересечения касательной с осью Ox). Значит 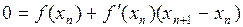. Разрешая это уравнение относительно 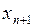, находим

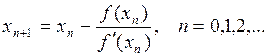(2.6)

Полученная рекуррентная формула (2.6) определяет сходящуюся к 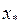числовую последовательность. Погрешность приближенного к 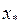значения 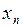определяется из неравенства, установленного в работах [2], [3]:

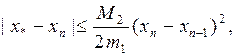(2.7)

где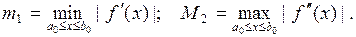

Метод хорд

Пусть корень уравнения (2.1) отделен на начальном отрезке 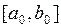, причем 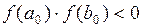и существуют и знакопостоянны 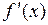и 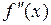для всех 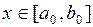. Геометрический смысл метода хорд состоит в том, что к графику функции 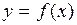на отрезке, внутри которого находится корень, проводится стягивающая его хорда и вместо точки пересечения графика 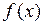с осью Ox ищется уже точка пересечения этой хорды с осью Ox. В качестве начального приближения 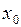к корню 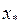выбирается тот из концов отрезка 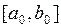, в котором функция 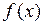и ее вторая производная имеют противоположные знаки, т. е.

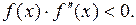(2.8)

При этом противоположный конец отрезка 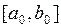будет неподвижен. Этот неподвижный конец отрезка обозначим через C (рис. 2.4). Строя последовательно указанным выше способом хорды и находя их точки пересечения с осью Ox, получаем последовательность приближений искомого корня

,

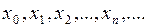которая при выполнении отмеченных в начале параграфа условий, будет сходиться к корню уравнения (2.1).

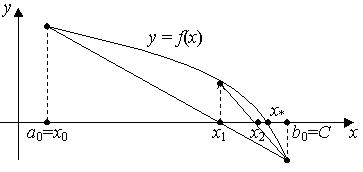
Рис. 2.4. Геометрическая иллюстрация метода хорд

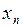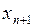Получим расчетную формулу для метода хорд. Пусть и – предыдущее и последующее приближения корня, C – неподвижная точка. Запишем уравнение прямой (хорды), проходящей через две точки с координатам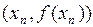и и 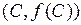. Получим

.

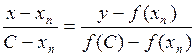В уравнении положим 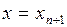, тогда 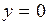и уравнение примет вид

.

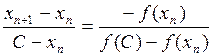Разрешая это уравнение относительно 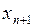, получим рекуррентную формулу для последовательности приближений корня уравнения (2.1)

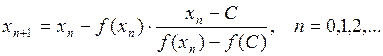(2.9)

При этом погрешность приближения на n-ом шаге определяется следующим неравенством [2], [3]:

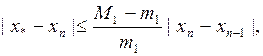(2.10)

где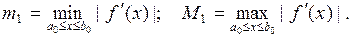

Комбинированный метод

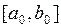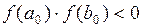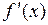Пусть корень уравнения (2.1) отделен на начальном отрезке , причем и и 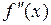отличны от нуля и знакопостоянны на этом отрезке. Сравнивая условия выбора начального приближения 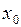в методах Ньютона и хорд, несложно заметить, что для одного и того же уравнения в качестве начальных приближений выбираются разные концы отрезка 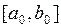. Учитывая это обстоятельство, можно одновременно приближать к 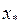оба конца начального отрезка. При этом один конец отрезка будет уточняться методом Ньютона, а другой – методом хорд. Такой метод решения уравнения называется комбинированным. Геометрическая иллюстрация этого метода дана на рис. 2.5.

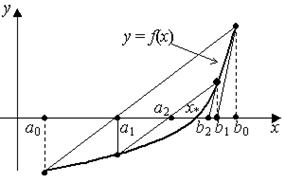
Рис. 2.5. Геометрическая иллюстрация комбинированного метода

Формулы, реализующие комбинированный метод решения уравнения (2.1), вытекают из формул (2.6) и (2.9).

Если выполняется условие 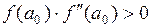, то уточнение отрезка 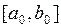ведется по формулам:

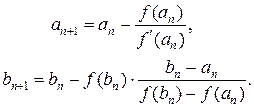(2.11)

Если же выполняется условие 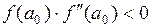, то уточнение отрезка 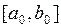ведется по формулам:

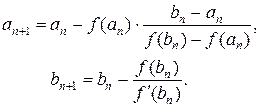(2.12)

Процесс вычисления по формулам (2.12) и (2.13) продолжается до тех пор, пока на некотором шаге n не будет выполняться неравенство

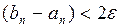. (2.13)

Тогда в качестве приближенного значения корня берется величина