Поняття про вбудовані функції маткада

Лабораторна робота № 3. Дії над матрицями у MathCad

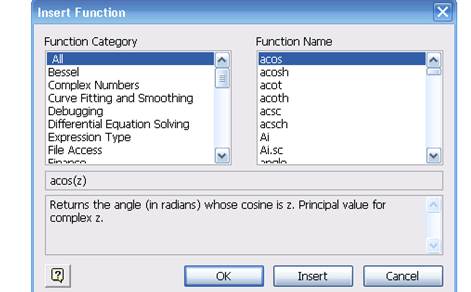Більшість задач у Маткаді вирішуються за допомогою так званих вбудованих функцій, тобто за допомогою заздалегідь складених програм розв’язку того чи іншого завдання. Кожна така програма має своє власне ім'я, по якому вона викликається. Ім'я можна набирати з клавіатури, але можна і викликати за допомогою кнопки f(x) головного меню. Натиснувши цю кнопку, ми викличемо панель Insert Function (вставити функцію), в якій є два вікна: Function Category (тип функції) та Function Name (ім'я функції). Вибравши тип і ім'я, і натиснувши кнопку ОК, ми викличемо цю функцію (Рис.1).

Рис.1.Панель виклику функції

Нехай, наприклад, потрібно знайти синус числа 45. Викликавши панель вставки функції, виберемо категорію Trigonometric і назва sin, натиснемо ОК. На екрані з'явиться шаблон зі словом sin всередині і дужками. Вставивши в дужки число 45, натиснемо «=». Отримаємо sin (45) = 0.851. Можна було б набрати ліву частину на клавіатурі і, після натискання знаку =, отримати ту саму відповідь.

Аналогічно використовуються і інші вбудовані функції Маткада.

У Маткаді масиви можуть записуватися у вигляді векторів (одновимірні масиви), у вигляді матриць (двовимірні масиви) і у вигляді таблиць. Ми розглянемо поки тільки запис матриць і векторів. Для дій над ними є панель Matrix (матриця), показана на рис. 2.

Рис.2. Панель матриць

Для введення матриць і векторів натиснемо кнопку панелі матриць і викличемо цим вікно введення Insetrt Matrix (ввести матрицю), показане на рис.3.

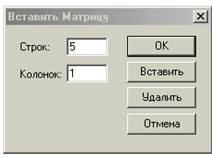
Рис.3. Вікно введення матриць і векторів. Рис.4. Шаблон

вектора.

При введенні вектора в графі columns (стовпці) слід проставити 1, а в графі rows (рядки) проставити розмір вектора. З'явиться шаблон, показаний на рис. 4.

Нижче представлено три п’ятиелементні масиви-вектори: Два з них - чисельні, третій - літерний, четвертий складається з виразів.

При заданні літерних масивів і масивів – виразів необхідно попередньо присвоювати їм чисельні значення (за кожною буквою в комп'ютері повинно стояти число). Після завдання виразів вектора можна, записавши його ім'я і поставивши знак =, отримати його значення. Малюнок зайвий раз ілюструє, що Маткад розрізняє рядкові і заголовні букви.

Над векторами, що показані на рис.5, визначені операції додавання, віднімання, транспонування, множення за математичними правилами множення матриць. Знак транспонування слід вводити з панелі Matrix (матриця).

Порядковий номер елемента, який є його адресою, називається індексом.

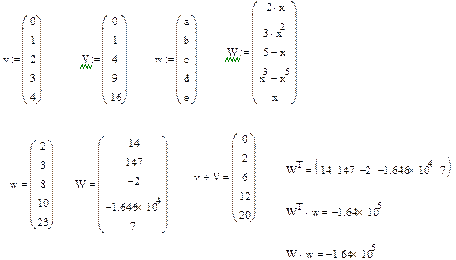Нижня межа індексації задається значенням системної змінної ORIGIN, яка може приймати значення 0 або 1. По замовчуванню прийнято 0.

Рис.5. Запис векторів у Маткад

Ім'я масиву пов'язане з іменами індексованих змінних, значеннями яких є елементи масиву. Для цього досить у вигляді підрядкового індексу вказати індекс елемента. Наприклад, якщо третій з представлених масивів має ім'я V, то його елементами при ORIGIN = 0 будуть індексовані змінні:

v₀ = 0 V₁ = 1, w₃ = d, W₄ = x.

При заданні ORIGIN = 1, отримаємо:

v₁ = 0, V₁ = 0, w₃ = c, W₄ = x³ - x⁵.

Завдання 1. Ввести всі вектори рис.5 і здійснити над ними всі дії, що наведені на малюнку. Матриці в Маткаді вводяться так само, як і вектори, але число стовпців у них - більше одиниці. Елементами матриці можуть бути також числа, букви, вирази. Як і у випадку векторів, літерні елементи і елементи – вирази повинні бути попередньо визначені чисельно. На рис.6 показано різні способи введення матриць.

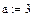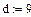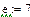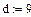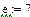
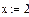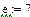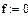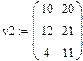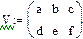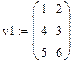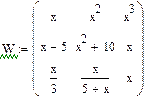
Рис.6. Введення матриць

Завдання 2. Ввести всі матриці, наведені на рис.6.

Елементи матриць є індексованими змінними, імена яких збігаються з іменами матриць. Для кожної індексованої змінної вказуються два індекси: один - для номера рядка, інший - для номера стовпця. Наприклад, для матриці W середній елемент позначається як W_1,1 а останній як W_2,2. (Індекси набираються через кому). На рис.7 показано зміну індексації при різних значеннях змінної ORIGIN. (Набирається обов'язково заголовними буквами).

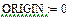
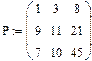
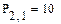
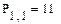
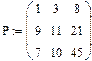
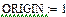
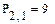
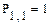
Рис.7. Роль змінної ORIGIN

У Маткаді визначені наступні дії над векторами і матрицями:

a. сумування - віднімання,

b. скалярне і векторне множення,

c. звернення,

d. транспонування,

e. сортування,

f. виділення стовпців.

Вони виконуються з використанням наступних кнопок панелі Matrix:

кнопка індексації елементів матриці,

кнопка звернення матриці,

кнопка скалярного добутку векторів і матриць

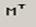
кнопка транспонування матриці,

кнопка векторного добутку двох векторів

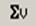кнопка додавання векторів

кнопка виділення стовпця матриці

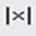
кнопка обчислення детермінанта матриці.

Завдання 3: Провести над матрицями всі дії, показані на рис.8 ..

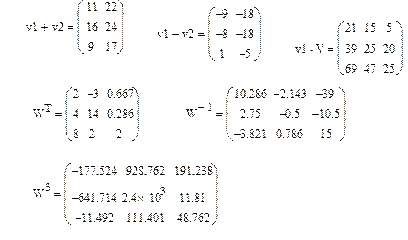
Рис.8. Дії над матрицями

Завдання 4: Ввести дві довільні матриці. Перемножити. Наприклад:

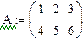
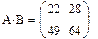
Перевірте на папері правильність зроблених вище дій

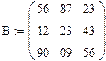
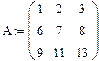
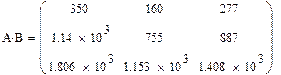
Рис.9. Приклад виконання завдання 4

Звернення та обчислення визначника можливо тільки для квадратних матриць.

Завдання 5. Введіть довільну квадратну матрицю, знайдіть їй обернену та обчисліть визначник, використовуючи наведені вище кнопки вбудованих операторів.

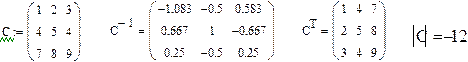Рис.10. Приклад виконання завдання 5 .

Як відомо, множення матриці на обернену дає одиничну матрицю. Перевіримо, чи правильно було проведено обертання

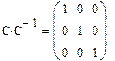
Завдання 6. Знайти скалярний і векторний добуток двох заданих трьохелементних векторів: Перевірити на папері правильність обчислень.

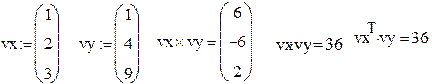Рис.11.Приклад виконання завдання 6.

Перевіримо правильність скалярного множення, перемноживши vx^Т і vy. Отримали також 36.

При розгляді матриць великих розмірів зручно виділяти їх стовпці.

Завдання 7. Використовуючи кнопку виділення стовпців, виділіть другий стовпець довільної матриці, наприклад:

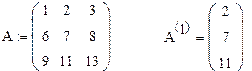Рис.12.Приклад виконання завдання 7.

У Маткаді є велика кількість вбудованих функцій для дій над матрицями та векторами. Розглянемо деякі з них.

Обчислення максимального і мінімального елементів матриці або вектора проводиться за допомогою вбудованих функцій Max (A) і Min (A).

Завдання 8. Обчислити максимальний та мінімальний елемент довільної матриці, наприклад:

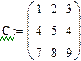
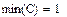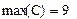Рис13. Обчислення максимального і мінімального елемента матриці.

Знати кількість стовпців і рядків в матриці дуже зручно для перевірки дій над багатовимірними матрицями і векторами. Вони знаходяться за допомогою вбудованих функцій Cols(A) – число стовпців матриці А і Rows(A) – число рядків матриці А

Завдання 9. Визначити число рядків і стовпців у довільній матриці, наприклад

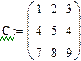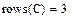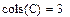Рис.13. Приклад виконання завдання 9.

Одинична матриця розміром N формується убудованою функцією Idenfity (N), а слід матриці - вбудованою функцією. tr (A):

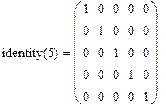
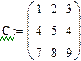
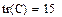
Рис.14. Формування одиничної матриці і обчислення сліду матриці.