Синусоидальном токе комплексным методом
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ УСТАНОВИВШЕМСЯ
Непосредственное использование для расчета цепей синусоидального тока законов Кирхгофа связано с громоздкими и трудоемкими вычислениями.
Существенное упрощение расчета достигается с помощью изображения синусоидальных функций времени комплексными числами. Метод, основанный на символическом изображении действительных синусоидальных функций времени комплексными числами, будем называть комплексным методом.
Комплексный метод был введен в теорию переменных токов американским ученым и инженером Ч.П. Штейнметцем, а затем в России академиком В.Ф. Миткевичем.
Комплексное число 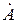 может быть записано в алгебраической, показательной и тригонометрической формах, соответственно:
может быть записано в алгебраической, показательной и тригонометрической формах, соответственно:
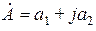 ,
, 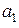 - вещественная часть,
- вещественная часть, 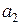 - мнимая часть комплексного числа;
- мнимая часть комплексного числа;
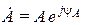 ,
, 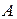 - модуль,
- модуль, 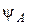 - аргумент комплексного числа;
- аргумент комплексного числа;
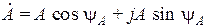 .
.
Здесь и далее 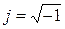 - принятое в электротехнике обозначение мнимой единицы.
- принятое в электротехнике обозначение мнимой единицы.
Соотношения между различными формами описания комплексного числа могут быть наглядно представлены с помощью изображения комплексного числа на комплексной плоскости.
В результате получим следующие формулы преобразования показательной формы записи комплексного числа в алгебраическую и обратно:
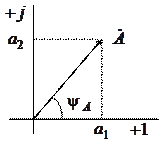
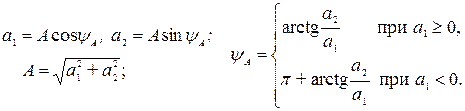
Заметим также, что
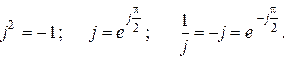
Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называются сопряженными. Для комплексного числа 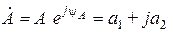 сопряженное ему комплексное число запишется в форме
сопряженное ему комплексное число запишется в форме 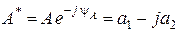 , причем
, причем 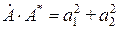 .
.
Синусоидально изменяющийся ток 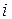 можно представить в форме
можно представить в форме 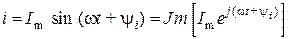 ,
,
так как
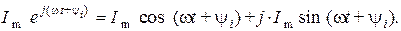
При этом комплексное число
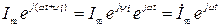
будем рассматривать как символическое изображение действительного синусоидального тока 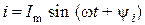 .
.
Заметим, что изображение синусоидального тока на комплексной плоскости тождественно изображению синусоидального тока на векторной диаграмме с помощью вектора 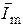 , вращающегося с частотой
, вращающегося с частотой 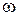 .
.
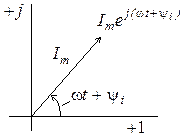
 Вводя знак изображения , запишем
Вводя знак изображения , запишем
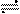
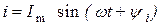
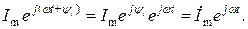
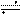 Отметим, что выражения, стоящие справа и слева от знака не равны между собой. Знак изображения лишь показывает, что между синусоидальной функцией времени и комплексным числом может быть установлено взаимно однозначное соответствие.
Отметим, что выражения, стоящие справа и слева от знака не равны между собой. Знак изображения лишь показывает, что между синусоидальной функцией времени и комплексным числом может быть установлено взаимно однозначное соответствие.
Будем называть далее действительную синусоидальную функцию оригиналом, а изображающую ее комплексную величину - изображением.
Комплексное число 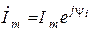 называют комплексной амплитудой тока. Аналогично,
называют комплексной амплитудой тока. Аналогично, 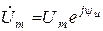 ,
, 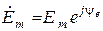 называют комплексными амплитудами напряжения и э.д.с. соответственно.
называют комплексными амплитудами напряжения и э.д.с. соответственно.
Разделив комплексные амплитуды на 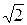 , получим комплексные действующие величины
, получим комплексные действующие величины
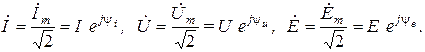
В дальнейшем комплексные действующие значения тока, напряжения или э.д.с. будем для краткости называть комплексными током, напряжением или э.д.с.
Рассмотрим примеры перехода от оригинала синусоидальной функции к ее комплексному изображению и обратный переход.
1. 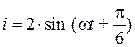 .
. 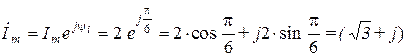 А.
А.
2. 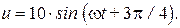
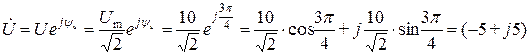 В.
В.
3. 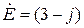 В.
В. 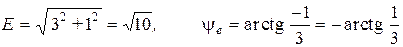 ,
,
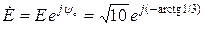 ,
,
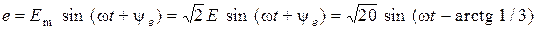 .
.
4. 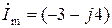 А.
А. 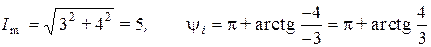 ,
,
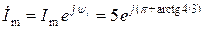 ,
, 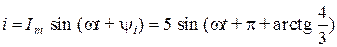 .
.
Получим выражение для изображения производной по времени от синусоидальной функции, например, синусоидального тока
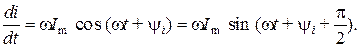
Изображение данной синусоидальной функции будет иметь вид
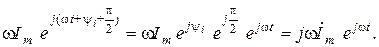
Таким образом,
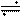
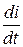
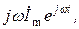
то есть операция взятия производной от действительной функции заменяется умножением на 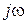 ее комплексного изображения.
ее комплексного изображения.
Получим теперь изображение для интеграла от синусоидальной функции из выражения для заряда
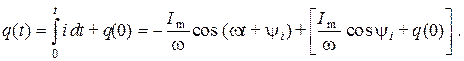 Так как рассматриваются только случаи, когда приложенное к зажимам цепи напряжение и э.д.с., действующие в цепи, синусоидальны и не содержат постоянных составляющих, то напряжения и заряды на конденсаторах также не содержат постоянных составляющих и соответственно
Так как рассматриваются только случаи, когда приложенное к зажимам цепи напряжение и э.д.с., действующие в цепи, синусоидальны и не содержат постоянных составляющих, то напряжения и заряды на конденсаторах также не содержат постоянных составляющих и соответственно 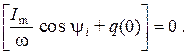
Следовательно,
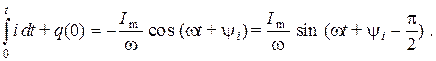
Искомое изображение будет иметь вид
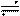
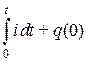
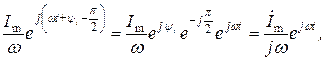
то есть операция интегрирования действительной функции заменяется делением на 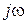 ее комплексного изображения.
ее комплексного изображения.
Таким образом, комплексный метод является методом алгебраизации уравнений цепи. Сущность его заключается в том, что все заданные функции времени заменяются их комплексными изображениями, при этом интегро-дифференциальные уравнения, составленные по законам Кирхгофа, переходят в алгебраические уравнения относительно комплексных переменных. Решая эти уравнения, находим комплексные выражения искомых функций и от них переходим к оригиналам этих функций.
В качестве примера рассмотрим цепь, состоящую из с 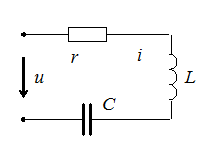 оединенных последовательно резистора, катушки индуктивности и конденсатора, к зажимам которой приложено напряжение
оединенных последовательно резистора, катушки индуктивности и конденсатора, к зажимам которой приложено напряжение 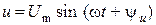 . Считая параметры r, L, C известными, определим ток
. Считая параметры r, L, C известными, определим ток 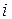 в цепи.
в цепи.
Уравнение Кирхгофа для данной цепи имеет вид
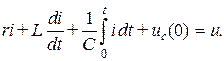
Перейдя к комплексным изображениям, получим алгебраическое уравнение в комплексной форме
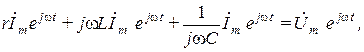
откуда
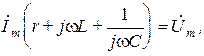
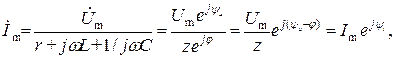
где 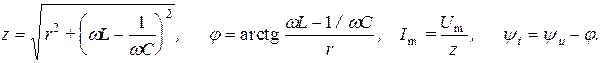
Таким образом, определены амплитуда 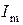 и начальная фаза
и начальная фаза 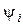 искомого тока в выражении
искомого тока в выражении 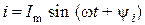 .
.
Поскольку все токи и напряжения в цепи изменяются с частотой 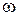 , равной частоте приложенного напряжения, то в дальнейшем при использовании комплексного метода расчета множитель
, равной частоте приложенного напряжения, то в дальнейшем при использовании комплексного метода расчета множитель 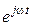 будем опускать.
будем опускать.
