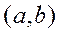Интегральный признак Коши

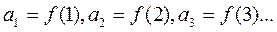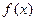Пусть члены «+» ряда таковы, что , где при 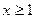непрерывн., «+» и убывает, тогда исх. ряд 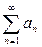и несобств. интеграл 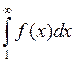сходятся и расходятся одновременно.

Знакочередующиеся ряды.

Знакочеред. рядом наз ряд вида , где . Этот ряд можно записать в виде

Признак Лейбница.

Если члены знакочеред. ряда удовлетворяют условиям:

1,

2,

то знакочеред. ряд сходится.

Абсолютная и условная сходимость.

Ряд (1) наз абсолютно сход, если сходится ряд (2). Если же ряд (1) сх, а ряд (2) расх., то такие ряды наз условно сходящимися. 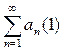и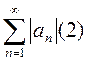

Теорема:если ряд сходится абсолютно, то он сходится.

Если ряд с произвольными членами расходится, то члены данного ряда можно расставить таким образом, что ряд будет сходиться к любому наперед заданному числу.

Функциональные ряды.

Ряды, членами к-рых явл. функции наз функциональным рядом.

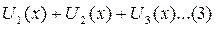
Если вместо переменной положить 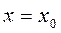, где 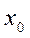–из обл. определения ф-и 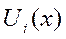, то получим числовой ряд 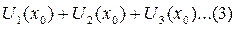. Если данный ряд сходится, то наз. точкой сходимости, если числ. ряд расходится. то 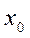–точка расходимости.

Совокупность всех точек сходимости функ. ряда наз обл его сходимости.

Степенные ряды.-функциональный ряд вида 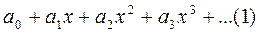, где 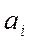–действит. числа, называемые коэф-тами степенного ряда.

1. если степенной ряд сходится только в т. 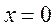, то его будем относить к рядам 1-го класса.

2. ряд (1) сходящийся в любой точке, будем относить к рядам 2-го рода.

3. ряд, не Î к 1-му и 2-му классу относят к рядам 3-го класса.

Теорема Авеля: если степенной ряд (1) сходится при 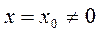, то он абсолютно сходится для любого 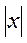< 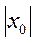. Если же степ. ряд (1) расходится при 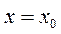, то он расходится и при всех > .

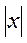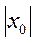След-но для каждого степенного ряда(1) третьего класса сущ-ет число 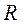>0, называемое радиусом сходимости, для к-рого вып-тся условия: при 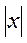< 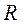ряд сходится абсолютно , при 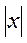> 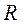–расходится. Промежуток 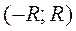наз интервалом сходимости степ. ряда. Для степ. ряда 2-го класса инт. сходимости (-¥;+¥). Областью сходимости степ. ряда явл. интервал, к-рому в отдельном случае добавляются один или оба конца этого интервала. Для степенного ряда 1-го класса полагают 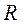=0, 2-го класса =¥.

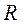Теорема. Пусть для степенного ряда сущ-ет и оличен от 0 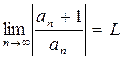, тогда .

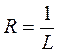Вопрос №35. Комплексные числа.

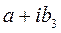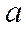О. Комплексное число-выраж-е вида , где и 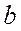–действит. числа, а символ 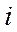удовлетворяет условию .

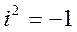Положим, что квадрат этого выраж-я равен -1, число 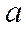наз. действит. частью, 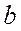* 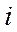мнимой частью, 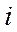-мнимая ед. комплексного числа.

Множ-во всех комплексных чисел обознач. .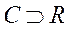

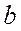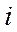* наз. чисто мнимым. Два комплексных числа наз. равными, если равны соотв. их действ. и мнимые части.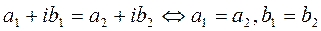

Числа вида 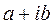, 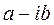–комплексно сопряженные и обозначаются соотв-нно 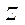и 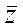. Очевидно, что каждому комплексному числу 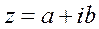соотв-ет единствен. т. на плоскости с коорд.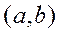

Плоскость по 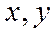–комплексная. Оси Ох и Оу соотв-но действительная и мнимая. , ®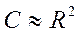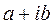