Самостійна робота студентів
Варіант №1
I семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
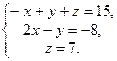 .
.
2. Знайти власні значення і власні вектори матриці:
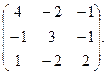
3. 1) Знайти косинус кута між векторами 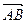 і
і 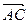 .
. 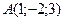 ,
, 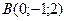 ,
, 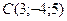 .
.
2) Обчислити об’єм тетраедра з вершинами в точках 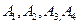 і його висоту, опущену із вершини
і його висоту, опущену із вершини 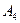 на грань
на грань 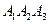 .
. 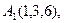
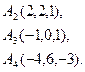
4. Прибуток від продажу 50 одиниць деякого товару становить 50 грн., 100 од. – 200 грн. Визначити прибуток від продажу 500 од. Товару, за умови, що функція прибутку лінійна.
5. Подані координати вершин трикутника АВС :А (- 2,1,2) В (-4,-5,3) С (4,-2,4). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 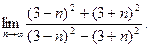 ; б)
; б) 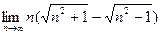 ; в)
; в) 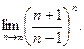 ; г)
; г) 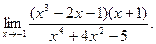 ; д)
; д) 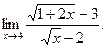
7. Продиференціювати вказані функції:
а) 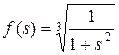 ; б)
; б) 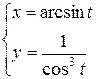 ; в)
; в) 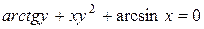 .
.
8. Провести повне дослідження функції і побудувати її графік:
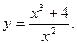
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 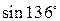 ; б)
; б) 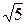 .
.
10. Знайти найбільше та найменше значення функції двох змінних:
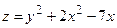 у замкнутій області, обмеженій еліпсом
у замкнутій області, обмеженій еліпсом 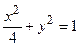 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 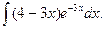 ; б)
; б) 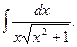 ; в)
; в) 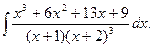
12. Знайти визначені інтеграли
а) 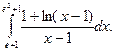 ; б)
; б) 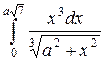 ; в)
; в) 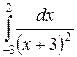 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
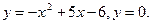
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин
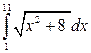 .
.
15. Знайти загальний інтеграл диференціального рівняння:
а) 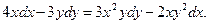 ; б)
; б) 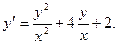 ;
;
в) 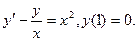 г)
г) 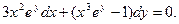
16. Знайти загальний розв’язок диференціального рівняння:
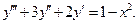
17. Обчислити 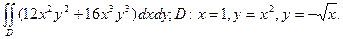
18. Дослідити на збіжність ряд:
а) 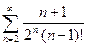 ; б)
; б) 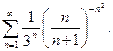 ; в)
; в) 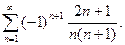
19. Знайти область збіжності ряду: 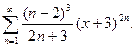
20. Позичку у 80 тис. грн. надано на півроку під 8% річних. Визначити ставку простих відсотків, що враховує інфляцію, та суму платежу, якщо річний індекс інфляції 110,1%.
Варіант №2
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
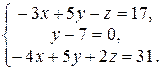
2. Знайти власні значення і власні вектори матриці: 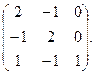
3. 1) Знайти косинус кута між векторами 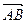 і
і 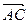 .
.
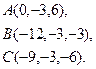
2) Обчислити об’єм тетраедра з вершинами в точках 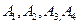 і його висоту, опущену із вершини
і його висоту, опущену із вершини 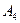 на грань
на грань 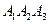 .
.
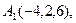
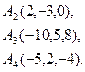
4. Витрати виробництва 100 одиниць деякого товару складають 300 грн., а 500 одиниць – 600 грн. Визначити витрати виробництва 400 од. товару за умови, що функція витрат є лінійною.
5. Подані координати вершин трикутника АВС: А (- 4,1,1), В (1,10,2), С (8,3,4). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 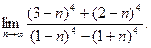 ; б)
; б) 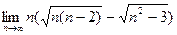 ; в)
; в) 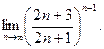 ; г)
; г) 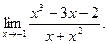 ; д)
; д) 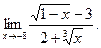
7. Продиференціювати вказані функції:
а) 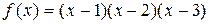 ; б)
; б) 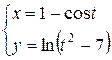 ; в)
; в) 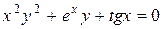 .
.
8. Провести повне дослідження функції і побудувати її графік:
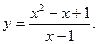
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 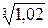 ; б)
; б) 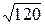 .
.
10. Знайти найбільше та найменше значення функції двох змінних:
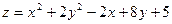 у замкнутім трикутнику, обмеженому осями координат і прямою
у замкнутім трикутнику, обмеженому осями координат і прямою 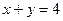 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 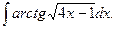 ; б)
; б) 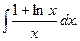 ; в)
; в) 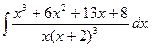
12. Знайти визначені інтеграли
а) 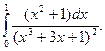 ; б)
; б) 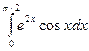 ; в)
; в) 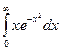 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
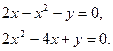
14. Обчислити інтеграли наближено за формулою Сімпсона відрізок [a,b] поділити на 10 частин
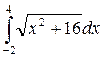 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 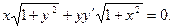 ; б)
; б) 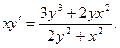 ;
;
в) 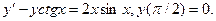 ; г)
; г) 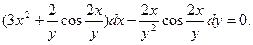
16. Знайти загальний розв’язок диференціального рівняння:
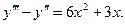
17. Обчислити 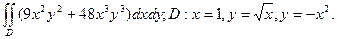
18. Дослідити на збіжність ряд:
а) 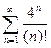 ; б)
; б) 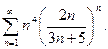 ; в)
; в) 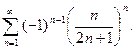 ;
;
19. Знайти область збіжності ряду: 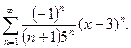
20. Річний кредит розміром 200 тис. грн. видано під просту декурсивну ставку 12%. Визначити суму відсоткових грошей і кінцеву суму боргу.
Варіант №3
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
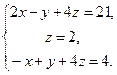
2. Знайти власні значення і власні вектори матриці:
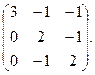
3. 1) Знайти косинус кута між векторами 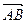 і
і 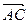 .
.
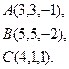
2) Обчислити об’єм тетраедра з вершинами в точках 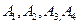 і його висоту, опущену із вершини
і його висоту, опущену із вершини 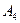 на грань
на грань 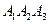 .
. 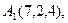
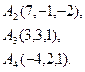
4. Витрати перевезення двома транспортними засобами виражаються функціями 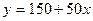 і
і 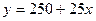 , де
, де 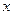 - відстань перевезення в сотнях кілометрів, а
- відстань перевезення в сотнях кілометрів, а 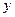 - транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
- транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
5. Подані координати вершин трикутника АВС: А (- 1,5,3), В (2,0,2), С (6,8,1). Знайти: а) довжину та рівняння медіани СЕ; б) довжину висоти АД; в) внутрішній кут С у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АС.
6. Обчислити границі:
а) 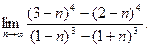 ; б)
; б) 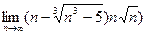 ; в)
; в) 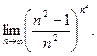 ; г)
; г) 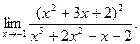 ; д)
; д) 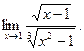
7. Продиференціювати вказані функції:
а) 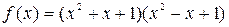 ; б)
; б) 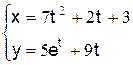 ; в)
; в) 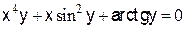 .
.
8. Провести повне дослідження функції і побудувати її графік:
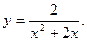
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 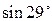 , б)
, б) 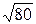 .
.
10. Знайти найбільше та найменше значення функції двох змінних: 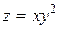 у крузі
у крузі 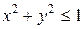 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 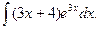 ; б)
; б) 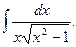 ; в)
; в) 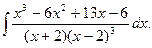
12. Обчислити визначені інтеграли:
a) 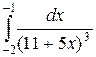 ; б)
; б) 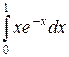 ; в)
; в) 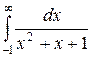 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
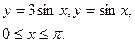
14. Обчислити інтеграли наближено за формулою Сімпсона відрізок [a,b] поділити на 10 частин 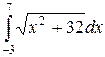 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 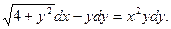 ; б)
; б) 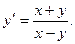 ;
;
в) 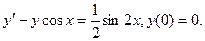 ; г)
; г) 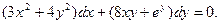
16. Знайти загальний розв’язок диференціального рівняння:
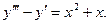
17. Обчислити 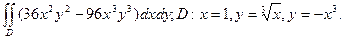
18. Дослідити на збіжність ряд:
а) 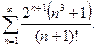 ; б)
; б) 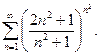 ; в)
; в) 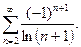
19. Знайти область збіжності ряду: 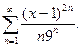
20. Яку суму отримав у розпорядження боржник, якщо він сплатив кредитору 24000 грн. за 2 роки під декурсиівну ставку 20% річних простих?
Варіант № 4
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
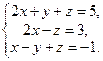
2. Знайти власні значення і власні вектори матриці:
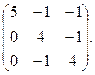
3. 1) Знайти косинус кута між векторами 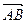 і
і 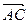 .
.
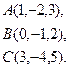
2) Обчислити об’єм тетраедра з вершинами в точках 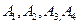 і його висоту, опущену із вершини
і його висоту, опущену із вершини 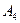 на грань
на грань 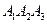 .
.
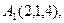
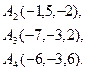
4. Прибуток від продажу деякого товару в двох магазинах виражається функціями 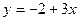 і
і 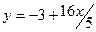 , де
, де 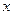 - лількість товару в сотнях штук, а
- лількість товару в сотнях штук, а 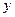 - прибуток в тисячах гривень. Визначити, починаючи з якої кількості товару більш вигідним становиться прожад у другому магазині.
- прибуток в тисячах гривень. Визначити, починаючи з якої кількості товару більш вигідним становиться прожад у другому магазині.
5. Подані координати вершин трикутника АВС:А (3,7,1), В (1,1,2),С (0,4,3). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01;г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 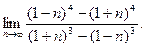 ; б)
; б) 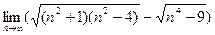 ; в)
; в) 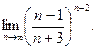 ; г)
; г) 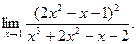 ; д)
; д) 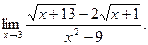
7. Продиференціювати вказані функції:
а) 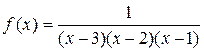 ; б)
; б) 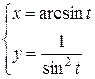 ; в)
; в) 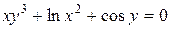 .
.
8. Провести повне дослідження функції і побудувати її графік:
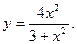
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 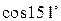 ; б)
; б) 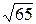 .
.
10. Знайти найбільше та найменше значення функції двох змінних:
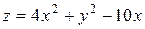 у замкнутій області, обмеженій гіперболою
у замкнутій області, обмеженій гіперболою 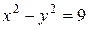 та прямою
та прямою 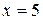 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 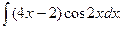 ; б)
; б) 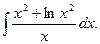 ; в)
; в) 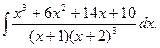
12. Знайти визначені інтеграли
а) 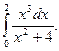 ; б)
; б) 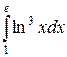 ; в)
; в) 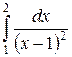 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
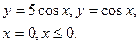
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин
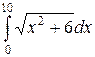 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 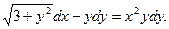 ; б)
; б) 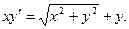 ;
;
в) 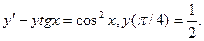 ; г)
; г) 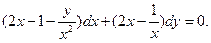
16. Знайти загальний розв’язок диференціального рівняння:
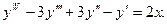
17. Обчислити 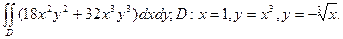
18. Дослідити на збіжність ряд:
а) 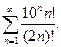 ; б)
; б) 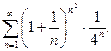 ; в)
; в) 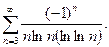
19. Знайти область збіжності ряду: 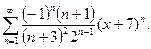
20. Надано 3-річний споживчий кредит на суму 360 тис. грн. під 45% річних за умови щомісячного погашення. Визначити суму щомісячного платежу та кінцеву суму боргу.
Варіант №5
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
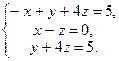
2. Знайти власні значення і власні вектори матриці:
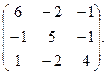
3. 1) Знайти косинус кута між векторами 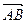 і
і 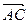 .
.
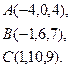
2) Обчислити об’єм тетраедра з вершинами в точках 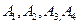 і його висоту, опущену із вершини
і його висоту, опущену із вершини 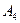 на грань
на грань 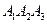 .
.
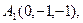
4. Прибуток від продажу 10 одиниць деякого товару становить 50 грн., 20 од. – 200 грн. Визначити прибуток від продажу 100 од. Товару, за умови, що функція прибутку лінійна.
5. Подані координати вершин трикутника АВС: А(-2,5,1), В(4,3,2), С(5,6,3). Знайти: а) довжину та рівняння медіани СЕ; б) довжину висоти АД; в) внутрішній кут С у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АС.
6. Обчислити границі:
а) 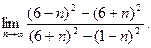 ; б)
; б) 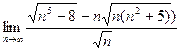 ;
;
в) 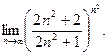 ; г)
; г) 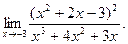 ; д)
; д) 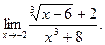
7. Продиференціювати вказані функції:
а) 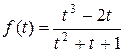 ; б)
; б) 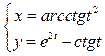 ; в)
; в) 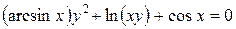 .
.
8. Провести повне дослідження функції і побудувати її графік:
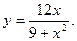
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 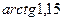 ; б)
; б) 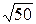 .
.
10. Знайти найбільше та найменше значення функції двох змінних:
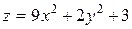 у замкнутій області, обмеженій еліпсом
у замкнутій області, обмеженій еліпсом 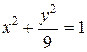 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 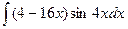 ; б)
; б) 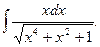 ; в)
; в) 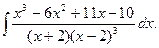
12. Знайти визначені інтеграли
а) 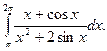 ; б)
; б) 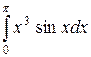 ; в)
; в) 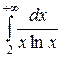 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
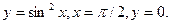
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок поділити на 10 частин 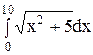 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 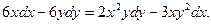 ; б)
; б) 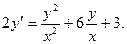 ;
;
в) 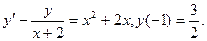 ; г)
; г) 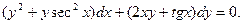
16. Знайти загальний розв’язок диференціального рівняння:
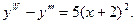
17. Обчислити 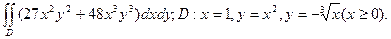
18. Дослідити на збіжність ряд:
а) 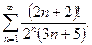 ; б)
; б) 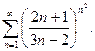 ; в)
; в) 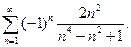
19. Знайти область збіжності ряду: 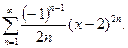
20. Надано споживчий кредит величиною 2000 грн. під 25% річних. Якою буде сума разового погашувального платежу, якщо планується сплачувати борг протягом одного року щоквартально.
Варіант №6
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
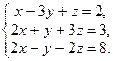
2. Знайти власні значення і власні вектори матриці:
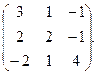
3. 1) Знайти косинус кута між векторами 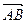 і
і 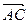 .
.
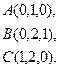
2) Обчислити об’єм тетраедра з вершинами в точках 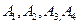 і його висоту, опущену із вершини
і його висоту, опущену із вершини 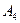 на грань
на грань 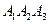 .
.
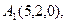
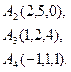
4. Витрати виробництва 20 одиниць деякого товару складають 100 грн., а 300 одиниць – 500 грн. Визначити витрати виробництва 100 од. товару за умови, що функція витрат є лінійною.
5. Подані координати вершин трикутника АВС: А (- 2,-3,1), В (2,1,2), С (6,-1,3). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут С у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 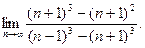 ;б)
;б) 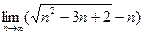 ;
;
в) 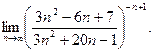 ; г)
; г) 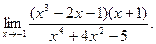 ;д)
;д) 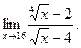
7. Продиференціювати вказані функції:
а) 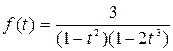 ; б)
; б) 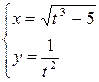 ; в)
; в) 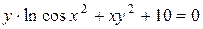 .
.
8.Провести повне дослідження функції і побудувати її графік:
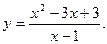
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 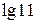 ; б)
; б) 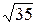 .
.
10. Знайти найбільше та найменше значення функції двох змінних:
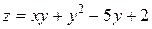 у замкнутій області, обмеженій параболою
у замкнутій області, обмеженій параболою 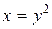 та прямою
та прямою 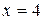 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 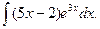 ; б)
; б) 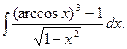 ; в)
; в) 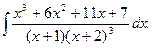
12. Знайти визначені інтеграли
а) 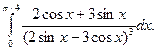 ; б)
; б) 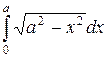 ; в)
; в) 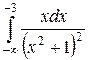 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
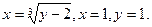
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин: 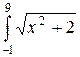 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 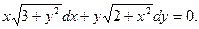 ; б)
; б) 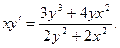 ;
;
в) 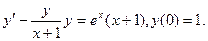 ; г)
; г) 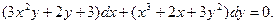
16. Знайти загальний розв’язок диференціального рівняння:
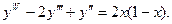
17. Обчислити 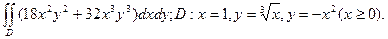
18. Дослідити на збіжність ряд:
а) 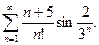 ; б)
; б) 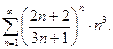 ; в)
; в) 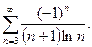
19. Знайти область збіжності ряду: 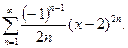
20. Позичку у 200 тис. грн. надано під 20% річних простих на 1 рік. Визначити суму відсотків та суму кінцевого платежу. Якою буде сума кінцевого платежу, якщо через 4 місяці ставку збільшили до 25%?
Варіант №7
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
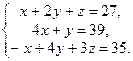
2. Знайти власні значення і власні вектори матриці:
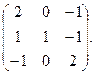
3. 1) Знайти косинус кута між векторами 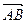 і
і 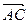 .
.
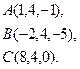
2) Обчислити об’єм тетраедра з вершинами в точках 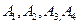 і його висоту, опущену із вершини
і його висоту, опущену із вершини 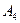 на грань
на грань 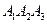 .
.
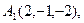
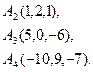
4. Витрати перевезення двома транспортними засобами виражаються функціями 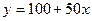 і
і 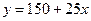 , де
, де 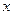 - відстань перевезення в сотнях кілометрів, а
- відстань перевезення в сотнях кілометрів, а 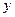 - транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
- транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
5. Подані координати вершин трикутника АВС: А (-3,3,1), В (3,10,2), С (4,7,4). Знайти: а) довжину та рівняння медіани СЕ;б) довжину висоти АД; в) внутрішній кут С у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АС.
6. Обчислити границі:
а) 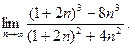 ; б)
; б) 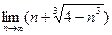 ; в)
; в) 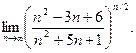 ; г)
; г) 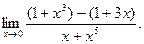 ; д)
; д) 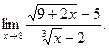
7. Продиференціювати вказані функції:
а) 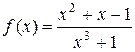 ; б)
; б) 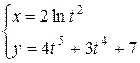 ; в)
; в) 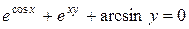 .
.
8. Провести повне дослідження функції і побудувати її графік:
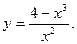
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 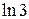 ; б)
; б) 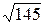 .
.
10.Знайти найбільше та найменше значення функції двох змінних: 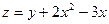 у замкнутій області, обмеженій параболою
у замкнутій області, обмеженій параболою 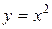 та прямою
та прямою 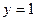 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 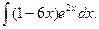 ; б)
; б) 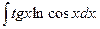 ; в)
; в) 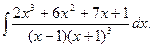
12. Знайти визначені інтеграли
а) 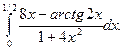 ; б)
; б) 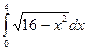 ; в)
; в) 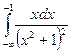 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
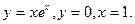
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин 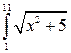 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 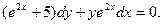 ; б)
; б) 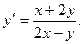 ; в)
; в) 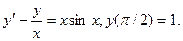 ; г)
; г) 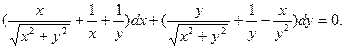
16. Знайти загальний розв’язок диференціального рівняння:
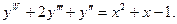
17. Обчислити 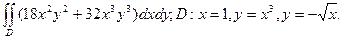
18. Дослідити на збіжність ряд:
а) 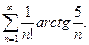 ; б)
; б) 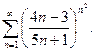 ; в)
; в) 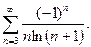 ;
;
19. Знайти область збіжності ряду 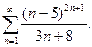
20. Якою буде кінцева сума боргу та відсотки, якщо в угоді передбачено за перші два роки нарахування 20% річних, а в наступні два роки ставка відсотків збільшується щорічно на 5%? Початкова сума боргу становить 100 тис. грн.
Варіант №8
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
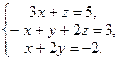
2. Знайти власні значення і власні вектори матриці:
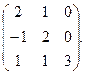
3. 1) Знайти косинус кута між векторами 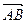 і
і 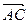 .
.
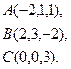
2) Обчислити об’єм тетраедра з вершинами в точках 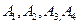 і його висоту, опущену із вершини
і його висоту, опущену із вершини 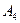 на грань
на грань 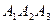 .
.
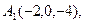
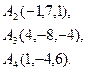
4. Прибуток від продажу деякого товару в двох магазинах виражається функціями 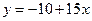 і
і 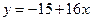 , де
, де 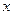 - кількість товару в сотнях штук, а
- кількість товару в сотнях штук, а 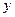 - прибуток в тисячах гривень. Визначити, починаючи з якої кількості товару більш вигідним становиться продаж у другому магазині.
- прибуток в тисячах гривень. Визначити, починаючи з якої кількості товару більш вигідним становиться продаж у другому магазині.
5. Подані координати вершин трикутника АВС :А (- 2,1,2) В (-4,-5,3) С (4,-2,4). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 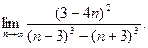 ; б)
; б) 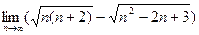 ; в)
; в) 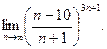 ; г)
; г) 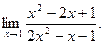 ; д)
; д) 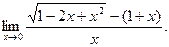
7. Продиференціювати вказані функції:
а) 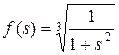 ; б)
; б) 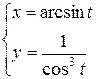 ; в)
; в) 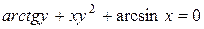 .
.
8. Провести повне дослідження функції і побудувати її графік:
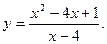
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 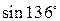 ; б)
; б) 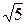 .
.
10.Знайти найбільше та найменше значення функції двох змінних:
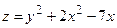 у замкнутій області, обмеженій еліпсом
у замкнутій області, обмеженій еліпсом 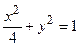 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 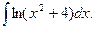 ; б)
; б) 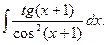 ; в)
; в) 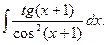
12. Знайти визначені інтеграли
а) 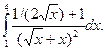 ; б)
; б) 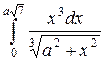 ; в)
; в) 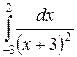 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
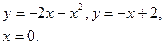
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин 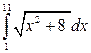 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 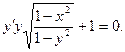 ; б)
; б) 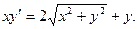 ; в)
; в) 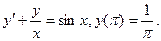 ; г)
; г) 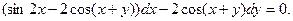
16. Знайти загальний розв’язок диференціального рівняння:
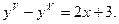
17. Обчислити 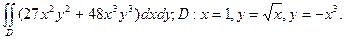
18. Дослідити на збіжність ряд:
а) 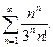 ; б)
; б) 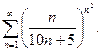 ; в)
; в) 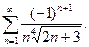
19. Знайти область збіжності ряду: 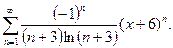
20. Позичку у 80 тис. грн. надано на півроку під 8% річних. Визначити ставку простих відсотків, що враховує інфляцію, та суму платежу, якщо річний індекс інфляції 110,1%.
Варіант №9
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
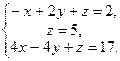
2. Знайти власні значення і власні вектори матриці:
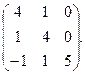
3. 1) Знайти косинус кута між векторами 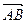 і
і 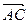 .
.
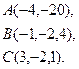
2) Обчислити об’єм тетраедра з вершинами в точках 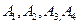 і його висоту, опущену із вершини
і його висоту, опущену із вершини 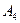 на грань
на грань 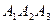 .
.
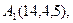
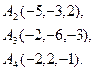
4. Прибуток від продажу 75 одиниць деякого товару становить 100 грн., 150 од. – 300 грн. Визначити прибуток від продажу 400 од. Товару, за умови, що функція прибутку лінійна.
5. Подані координати вершин трикутника АВС: А (0,4,2) В (5,8,3) С (7,2,4). Знайти: а) довжину та рівняння медіани СЕ; б) довжину висоти АД; в) внутрішній кут С у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АС.
6. Обчислити границі:
а) 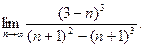 ; б)
; б) 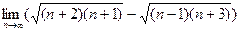 ;
;
в) 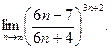 ; г)
; г) 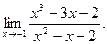 ; д)
; д) 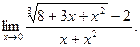
7. Продиференціювати вказані функції:
а) 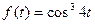 ; б)
; б) 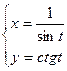 ; в)
; в) 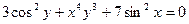 .
.
8.Провести повне дослідження функції і побудувати її графік:
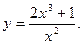
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 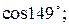 б)
б) 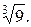
10.Знайти найбільше та найменше значення функції двох змінних: 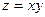 у крузі
у крузі 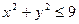 .
.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 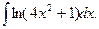 ; б)
; б) 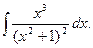 ; в)
; в) 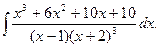
12. Знайти визначені інтеграли
а) 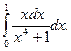 ; б)
; б) 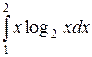 ; в)
; в) 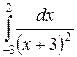 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
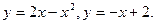
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин
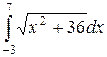 .
.
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 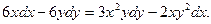 ; б)
; б) 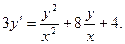 ; в
; в
) 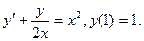 ; г)
; г) 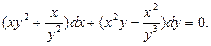
16. Знайти загальний розв’язок диференціального рівняння:
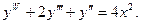
17. Обчислити 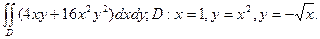
18. Дослідити на збіжність ряд:
а) 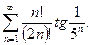 ; б)
; б) 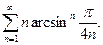 ; в)
; в) 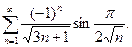
19. Знайти область збіжності ряду: 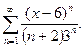
20. Нарощена сума склала 6 млн. грн., відсоткова ставка – 16% річних, строк зберігання грошей – 4 роки. Визначити первинну суму грошей за простими і складними відсотками.
Варіант №10
І семестр
1.Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
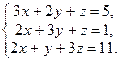
2. Знайти власні значення і власні вектори матриці:
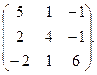
3. 1) Знайти косинус кута між векторами 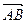 і
і 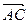 .
.
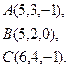
2) Обчислити об’єм тетраедра з вершинами в точках 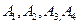 і його висоту, опущену із вершини
і його висоту, опущену із вершини 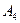 на грань
на грань 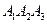 .
.
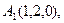
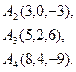
4. Витрати виробництва 100 одиниць деякого товару складають 150 грн., а 200 одиниць – 400 грн. Визначити витрати виробництва 200 од. товару за умови, що функція витрат є лінійною.
5. Подані координати вершин трикутника АВС: А (- 1,0,2), В (1,4,4), С (6,2,1). Знайти: а) довжину та рівняння медіани СЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АС.
6. Обчислити границі:
а) 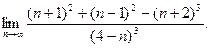 ; б)
; б) 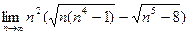 ;
;
в) 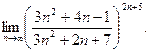 ; г)
; г) 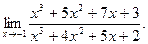 ; д)
; д) 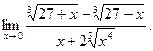
7. Продиференціювати вказані функції:
а) 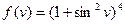 ; б)
; б) 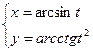 ; в)
; в) 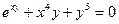 .
.
8.Провести повне дослідження функції і побудувати її графік:
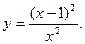
9. Замінивши приріст функції диференціалом, знайти наближено такі значення:
a) 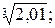 б)
б) 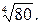
10.Знайти найбільше та найменше значення функції двох змінних: 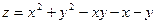 у замкнутім трикутнику, обмеженому прямою
у замкнутім трикутнику, обмеженому прямою 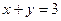 та осями координат.
та осями координат.
ІІ семестр
11. Знайти невизначені інтеграли:
а) 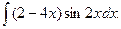 ; б)
; б) 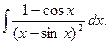 ; в)
; в) 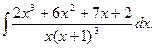
12. Знайти визначені інтеграли
а) 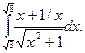 ; б)
; б) 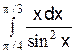 ; в)
; в) 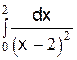 .
.
13. Обчислити об’єм тіла обертання, утвореного обертанням графіками функцій (вісь обертання Ох):
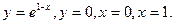
14. Обчислити інтеграли наближено за формулою Сімпсона, відрізок [a,b] поділити на 10 частин
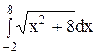
15. Знайти загальний інтеграл (розв’язок) диференціального рівняння:
а) 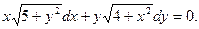 ; б)
; б) 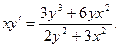 ;
;
в) 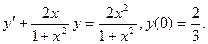 ; г)
; г) 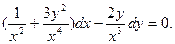
16. Знайти загальний розв’язок диференціального рівняння:
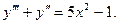
17. Обчислити 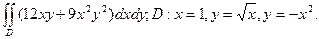
18. дослідити на збіжність ряд:
а) 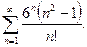 ; б)
; б) 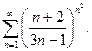 ; в)
; в) 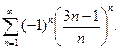
19. Знайти область збіжності ряду: 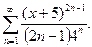
20. Вексель зі строком погашення 2 міс. і номіналом 900 тис. грн., за яким щомісячно нараховується 4% простих, куплений банком за місяць до строку за ставкою 36.4% річних. Якою була поточна вартість векселя?
Варіант №11
І семестр
1. Розв’язати систему рівнянь методом Гауса і за формулами Крамера:
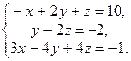
2. Знайти власні значення і власні вектори матриці:
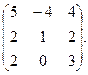
3. 1) Знайти косинус кута між векторами 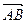 і
і 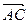 .
.
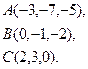
2) Обчислити об’єм тетраедра з вершинами в точках 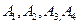 і його висоту, опущену із вершини
і його висоту, опущену із вершини 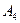 на грань
на грань 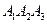 .
.
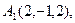
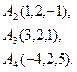
4. Витрати перевезення двома транспортними засобами виражаються функціями 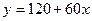 і
і 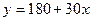 , де
, де 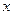 - відстань перевезення в сотнях кілометрів, а
- відстань перевезення в сотнях кілометрів, а 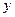 - транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
- транспортні витрати в грошових одиницях. Визначити, починаючи з якої відстані більш економічним стає другий транспортний засіб.
5. Подані координати вершин трикутника АВС:А (1,1,2), В (4,8,3), С (7,3,5). Знайти: а) довжину та рівняння медіани АЕ; б) довжину висоти АД; в) внутрішній кут В у радіанах з точністю до 0,01; г) площу трикутника; д) рівняння прямої , яка проходить через т. Е паралельно прямій АВ.
6. Обчислити границі:
а) 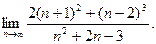 ; б)
; б) 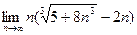 ; в)
; в) 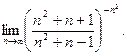 ; г)
; г) 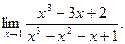 ; д)
; д) 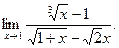
7. Продиференціювати вказані функції:
