Линейные однородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами
Линейные однородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами.
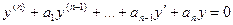 , где
, где 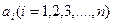 -действительные постоянные.(1)
-действительные постоянные.(1)
Уравнение 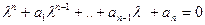 (2),полученное заменой производных
(2),полученное заменой производных 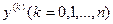 искомой функцией степенями
искомой функцией степенями 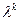 , называется характеристическим уравнением
, называется характеристическим уравнением
уравнения (2).Каждому действительному корню 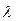 уравнения (2) кратностиr соответствуют r линейно независимых решений уравнения(1):
уравнения (2) кратностиr соответствуют r линейно независимых решений уравнения(1): 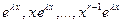 , а каждой паре комплексных корней
, а каждой паре комплексных корней 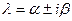 , кратности s соответствуют s пар линейно независимых решений :
, кратности s соответствуют s пар линейно независимых решений :
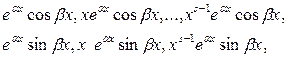
Если характеристическое уравнение имеет k действительных корней 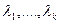 кратностей
кратностей 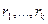 и l пар комплексно сопряжённых корней
и l пар комплексно сопряжённых корней 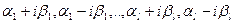 кратностей
кратностей 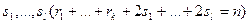 , то общее решение уравнения (1) запишется в виде
, то общее решение уравнения (1) запишется в виде
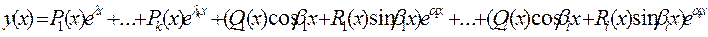 где
где 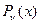 -произвольный многочлен степени
-произвольный многочлен степени 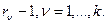 , а
, а 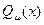 и
и 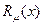 -произвольные многочлены степени
-произвольные многочлены степени 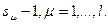
Для линейного однородного дифференциального уравнения с постоянными коэффициентами существует простой алгоритм построения фундаментальной системы решений. Будем искать решение уравнения в виде y(x) = 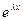 =
= 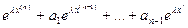
exp(lx)(n) + a1exp(lx)(n-1) + ... + an-1exp(lx)' + anexp(lx)=
= (ln + a1ln-1 + ... + an-1l + an)exp(lx) = 0,
т.е. число l является корнем характеристического уравнения
ln + a1ln-1 + ... + an-1l + an = 0.
Левая часть характеристического уравнения называется характеристическим многочленом линейного дифференциального уравнения:
P(l) = ln + a1ln-1 + ... + an-1l + an.
Таким образом, задача о решении линейного однородного уравнения n -го порядка с постоянными коэффициентами сводится к решению алгебраического уравнения.
Если характеристическое уравнение имеет n различных действительных корней
l1№ l2 № ... № ln,
то фундаментальная система решений состоит из функций
y1(x) = exp(l1x), y2(x) = exp(l2x), ..., yn(x) = exp(lnx),
и общее решение однородного уравнения имеет вид:
y(x)= c1 exp(l1x) + c2 exp(l2x) + ... + cn exp(lnx).
Если какой-либо из действительных корней характеристического уравнения повторяется r раз (r-кратный корень), то в фундаментальной системе решений ему отвечают r функций; если
lk=lk+1 = ... = lk+r-1,
то в фундаментальную систему решений уравнения входят r функций:
yk(x) = exp(lkx),
yk+1(x) = xexp(lkx),
yk+2(x) = x2exp(lkx), ...,
yk+r-1(x) =xr-1 exp(lnx).
Если характеристическое уравнение имеет комплексные корни, то каждой паре простых (имеющих кратность 1 ) комплексных корней
lk,k+1=ak ± ibk
в фундаментальной системе решений отвечает пара функций
yk(x) = exp(akx)cos(bkx), yk+1(x) = exp(akx)sin(bkx).
Если же комплексная пара корней имеет кратность r, то такой паре
lk=lk+1 = ... = l2k+2r-1=ak ± ibk,
в фундаментальной системе решений отвечают функции
exp(akx)cos(bkx), exp(akx)sin(bkx),
xexp(akx)cos(bkx), xexp(akx)sin(bkx),
x2exp(akx)cos(bkx), x2exp(akx)sin(bkx),
................
xr-1exp(akx)cos(bkx), xr-1exp(akx)sin(bkx).
Таким образом, для отыскания общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения l1, l2, ... , ln;
записать фундаментальную систему решений y1(x), y2(x), ..., yn(x);
записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x).
Билет38
