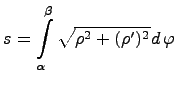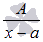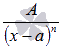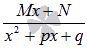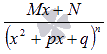Записать основные виды простейших дробей
Различают следующие виды простейших дробей:
где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля.
Называют их соответственно дробями первого, второго, третьего и четвертого типов.
10.Привести схему разложения рациональных функций на сумму простейших дробей.
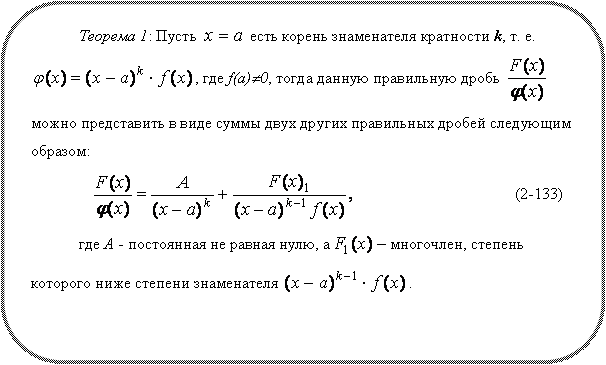
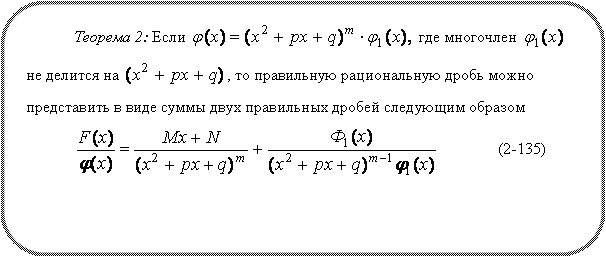
Сформулировать свойства неопределенного интеграла
Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то
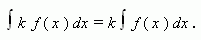
Короче: постоянную можно выносить за знак интеграла.
Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то
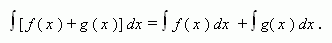
Короче: интеграл суммы равен сумме интегралов.
Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:
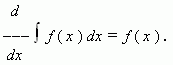
Короче: производная от интеграла равна подынтегральной функции.
Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
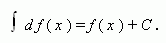
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
Знать таблицу основных неопределенных интегралов.
Знать таблицу производных
Записать формулу замены переменных в неопределенном интеграле
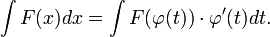
Записать формулу интегрирования по частям.
для неопределённого интеграла:
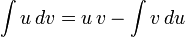
для определённого:
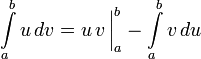
16.Объяснить метод внесения множителя под знак дифференциала.
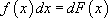, где 
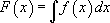, т.е. является первообразной 
.
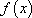17.Записать формулу Ньютона-Лейбница.
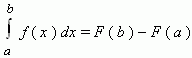
Записать формулы вычисления площадей плоских фигур с помощью определенного интеграла.
Площадь, заключённая между графиком непрерывной функции на интервале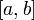 
и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
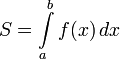
Площадь, заключённая между графиками двух непрерывных функций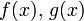 
на интервале 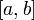находится как разность определённых интегралов от этих функций:
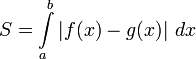
Записать формулы вычисления объемов тел с помощью определенного интеграла.
Объём тела вычисляется как определённый интеграл:
,
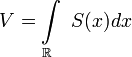где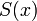 
— площадь горизонтального сечения тела с данной аппликатой 
.
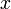Записать формулы вычисления длины дуги с помощью определенного интеграла.
Пусть известна функция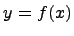 
и требуется найти длину дуги, заданной функцией 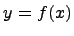, где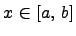 
.
Для определения длины дуги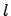 
необходимо вычислить определенный интеграл:
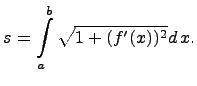
Рассмотрим случай параметрического задания кривой:
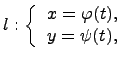
где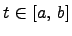 
. В этом случае для определения длина дуги 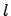вычисляется определенный интеграл:
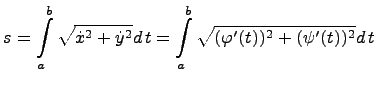
Рассмотрим случай, когда кривая задается в полярных координатах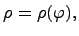 
где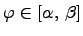 
. Тогда для определения длины дуги 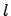вычисляется следующий определенный интеграл:
